先来看一道有意思题

situation

大意：

两个人玩井字棋，要求把所有位置填满后结束游戏。一方希望两者的连起来的线之差最多，一方希望最少。现在给定初始局面（已经存在一些棋子）以及先手，求最后的两者的连起来的线之差。

这就是一道对抗搜索的题目

什么是对抗搜索？简单来说，博弈双方对竞争相反的利益，一方使其最大化，一方使其最小化，那么我们就可以通过搜索来探索最终状态

min-max对抗搜索

假设我们已经有了一颗博弈树：
 

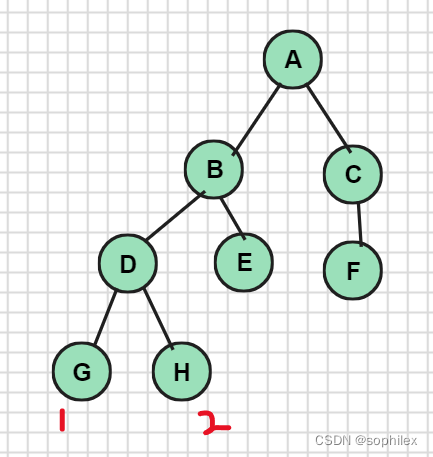
 如果我方先手且我方以最大化利益为目标，那么单数层就是我方的决策层，双数层就是对方的。那么在单数层的节点，它会选取利益最大化的子局面，反之亦然。

现在我们从最底层开始向上，D在单数层，它会选取最大的利益，所以它的利益为2。B就会在D和E的利益之间选取最小的...依次类推，最后我们就可以得到初始局面对应的利益了。

但是当博弈规模比较大的时候，搜索规模也会爆炸，就要考虑剪枝。

这里引入：

Alpha_Beta对抗搜索

我们限定一个利益区间【a,b】

α Alpha is the maximum lower bound of possible solutions 

对于一个追求max利益的节点P，它的所有子节点都是追求min利益，会将收益尽可能降低，那么P就会在所有尽可能低的收益里选最高的，也就是α了。

β Beta is the minimum upper bound of possible solutions

β同理。是在所有尽可能高的收益里取低

换句话说，α和β其实都是对应最差情况下的收益。

那么α会如何更新？显然被每一个子局面的最差情况更新，也就是子局面的β，同理β就会被子局面的α更新。

初始时a=-inf，b=inf（显然）

不难发现，对于一个追求最大收益的节点，如果它的子节点（都追求最小化收益）存在一个子局面，能够获得比a更小的收益，我们就可以剪掉对应子树，不然利益一定不会在区间范围内

同理，对于一个追求最小化收益的节点，如果子节点存在一个可以获得比b更大的收益，就要剪掉

否则我们的子节点就可以更新当前区间。区间不断缩小，最后确定收益值。

---

另外这里再考虑一下遍历的问题。显然一个父节点的区间端点要再子节点的端点里取极值，那么层序遍历（从下往上）就是不合理的，因为这样就还要去记录子节点的值。更好的是采用先序/后序遍历，就可以在搜索的时候完成更新了。

题解

最后讲回这题。

因为数据规模非常小，直接做min-max对抗搜索就可以了。对于每一个确定的局面我们可以很轻松就确定其对应的收益，那么剩余情况就暴力dfs就好了。然后为了区分情况方便记忆化，可以哈希一下。

code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int inf=0x3f3f3f3f;
const ll N=3e5+10;
string s;

struct ty//局面 
{
	char tr[5][5];
	bool judge(ll id,ll op)
	{
		if(op==0)//横排
		{
			for(int i=2;i<=3;++i)
			{
				if(tr[id][i]!=tr[id][i-1]) return 0;	
			}	
			return 1;
		} 
		else if(op==1)//竖排 
		{
			for(int j=2;j<=3;++j)
			{
				if(tr[j][id]!=tr[j-1][id]) return 0;
			}
			return 1;
		}
		else if(op==2)//斜着 
		{
			if(id==1)
			{
				for(int i=2;i<=3;++i)
				{
					if(tr[i][i]!=tr[i-1][i-1]) return 0;
				}
				return 1;
			} 
			else if(id==2)
			{
				for(int i=2;i<=3;++i)
				{
					if(tr[i][4-i]!=tr[i-1][5-i]) return 0;
				}
				return 1;
			}
		}
	}
	ll get_haxi()
	{
		ll haxi=0;//哈希值 
		for(int i=1;i<=3;++i)//三进制表示 
		{
			for(int j=1;j<=3;++j)
			{
				haxi*=3;
				if(tr[i][j]=='O') haxi++;
				else if(tr[i][j]=='X') haxi+=2;
			}
		}
		return haxi;
	}
	int get()
	{
		int ans=0;
		for(int i=1;i<=3;++i)
		{
			if(judge(i,0)==0) continue;
			else if(tr[i][1]=='O') ans++;
			else ans--;
		}
		for(int i=1;i<=3;++i)
		{
			if(judge(i,1)==0) continue;
			else if(tr[1][i]=='O') ans++;
			else ans--;
		}
		if(judge(1,2))
		{
			if(tr[1][1]=='O') ans++;
			else ans--;
		}
		if(judge(2,2))
		{
			if(tr[2][2]=='O') ans++;
			else ans--;
		}
		return ans;
	}
	bool jd()
	{
		for(int i=1;i<=3;++i)
		{
			for(int j=1;j<=3;++j)
			{
				if(tr[i][j]=='.') return 1;
			}
		}
		return 0;
	}
}; 
int dp[N][3];
int dfs(ty now,int op)
{
	int haxi=now.get_haxi();
	if(dp[haxi][op]!=-inf) return dp[haxi][op];
	if(!now.jd()) return now.get();//直接出结果
	if(op)//取max，最大化收益 
	{
		for(int i=1;i<=3;++i)
		{
			for(int j=1;j<=3;++j)
			{
				if(now.tr[i][j]=='.')//开始 
				{
					ty nex=now;
					nex.tr[i][j]='O';
					dp[haxi][op]=max(dp[haxi][op],dfs(nex,0));
				}	
			}	
		}	
	} 
	else
	{
		dp[haxi][op]=inf;
		for(int i=1;i<=3;++i)
		{
			for(int j=1;j<=3;++j)
			{
				if(now.tr[i][j]=='.')//开始 
				{
					ty nex=now;
					nex.tr[i][j]='X';
					dp[haxi][op]=min(dp[haxi][op],dfs(nex,1));
				}	
			}
		}
	}
	return dp[haxi][op];
}
void init()
{
	for(int i=0;i<=100000;++i)
	{
		for(int j=0;j<=1;++j)
		{
			dp[i][j]=-inf;
		}
	}
}
void solve()
{
	ll op;
	cin>>op;
	ty nd;
	for(int i=1;i<=3;++i)
	{
		for(int j=1;j<=3;++j)
		{
			cin>>nd.tr[i][j];
		}
	}
	cout<<dfs(nd,op)<<endl;
//    ty nd;
//    for(int i=1;i<=3;++i)
//    {
//    	for(int j=1;j<=3;++j)
//    	{
//    		nd.tr[i][j]='X';
//		}
//	}
//	cout<<nd.get()<<endl;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	init();
	ll t;cin>>t;while(t--)
	solve();
	return 0;
}