文章目录
- 1 概念
- 2 队列的使用
- 3 队列模拟实现
- 4 循环队列
- 4.1 循环队列 概念
- 4.1 循环队列模拟实现
- 5. 双端队列 (Deque)
- 6 用队列实现栈
- 7 用栈实现队列
1 概念
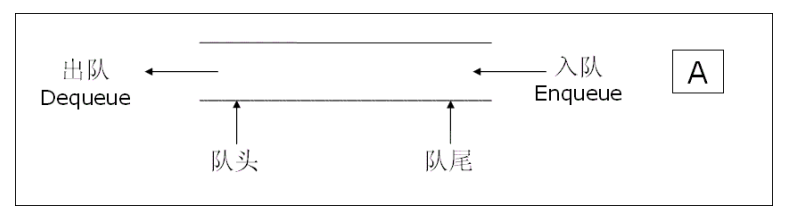
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(FirstIn First Out). 入队列:进行插入操作的一端称为队尾(Tail/Rear); 出队列:进行删除操作的一端称为队头(Head/Front)
2 队列的使用
在Java中,Queue是个接口,底层是通过链表实现的。
接口中提供的方法:

经常使用的方法:
| 方法 | 功能 |
|---|---|
| boolean offer(E e) | 入队列 |
| E poll() | 出队列 |
| E peek() | 获取队头元素 |
| int size() | 获取队列中有效元素个数 |
| boolean isEmpty() | 检测队列是否为空 |
注意:Queue是个接口,在实例化时必须实例化LinkedList的对象,因为LinkedList实现了Queue接口
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.offer(1);
q.offer(2);
q.offer(3);
q.offer(4);
q.offer(5); // 从队尾入队列
System.out.println(q.size());
System.out.println(q.peek()); // 获取队头元素
q.poll();
System.out.println(q.poll()); // 从队头出队列,并将删除的元素返回
if(q.isEmpty()){
System.out.println("队列空");
}else{
System.out.println(q.size());
}
}
3 队列模拟实现
队列中既然可以存储元素,那底层肯定要有能够保存元素的空间,通过前面线性表的学习了解到常见的空间类型有两种:顺序结构 和 链式结构。队列的实现使用链式结构较好,并且是双向链表。
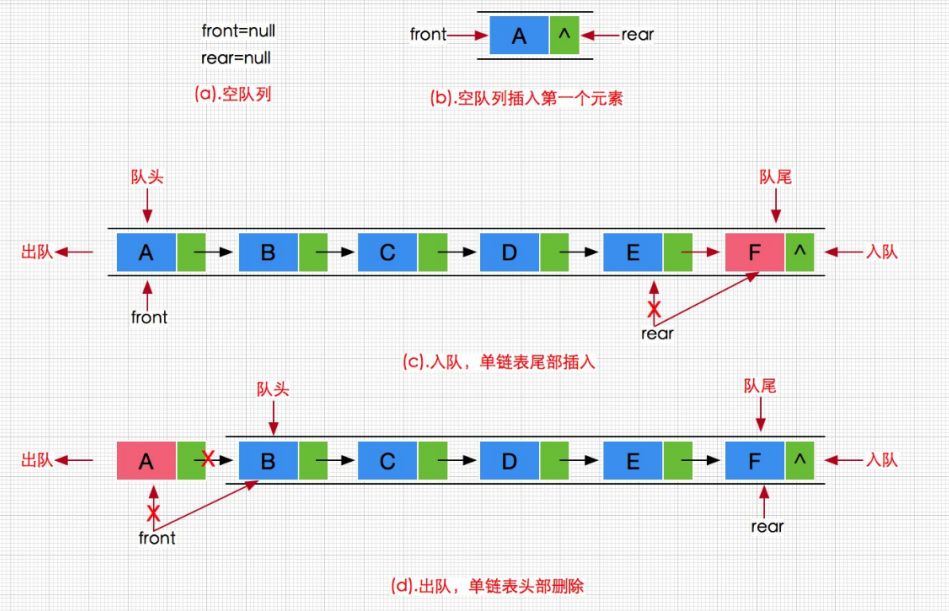
使用front标记队头,rear标记队尾
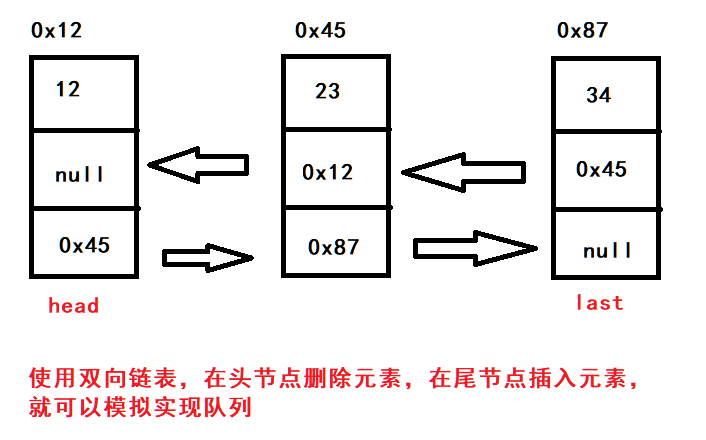
模拟实现一个双向链表,头节点first删除元素,尾节点last插入元素,可以模拟实现一个队列。
public class Queue {
// 双向链表节点
public static class ListNode{
ListNode next;
ListNode prev;
int value;
ListNode(int value){
this.value = value;
}
}
ListNode first; // 队头
ListNode last; // 队尾
int size = 0;
// 入队列---向双向链表位置插入新节点
public void offer(int e){
ListNode newNode = new ListNode(e);
if(first == null){
first = newNode;
// last = newNode;
}else{
last.next = newNode;
newNode.prev = last;
// last = newNode;
}
last = newNode;
size++;
}
// 出队列---将双向链表第一个节点删除掉
public int poll(){
// 1. 队列为空
// 2. 队列中只有一个元素----链表中只有一个节点---直接删除
// 3. 队列中有多个元素---链表中有多个节点----将第一个节点删除
int value = 0;
if(first == null){
return null;
}else if(first == last){
last = null;
first = null;
}else{
value = first.value;
first = first.next;
first.prev.next = null;
first.prev = null;
}
--size;
return value;
}
// 获取队头元素---获取链表中第一个节点的值域
public int peek(){
if(first == null){
return null;
}
return first.value;
}
public int size() {
return size;
}
public boolean isEmpty(){
return first == null;
}
}
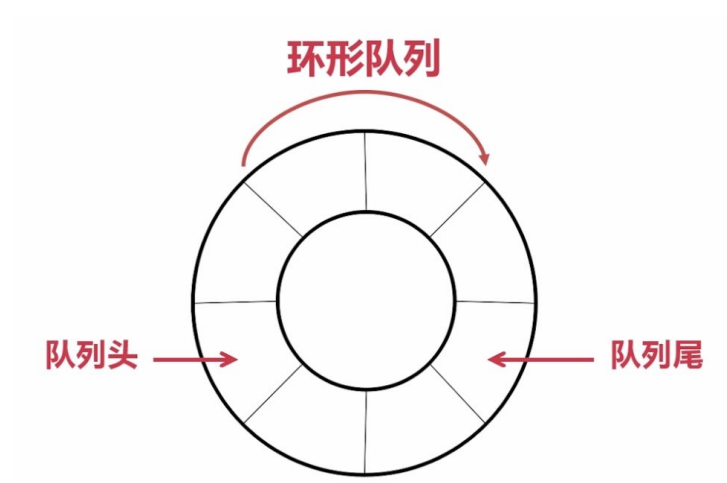
4 循环队列
4.1 循环队列 概念
那如果使用数组模拟实现队列呢?
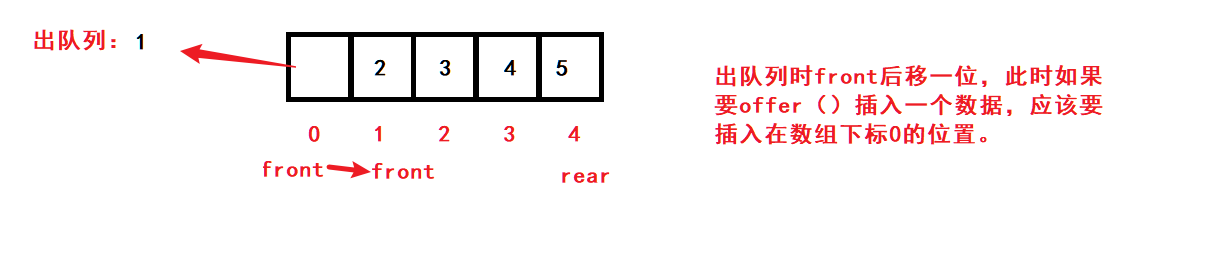
此时我们需要将数组看作是循环的,来实现在0下标插入数据,那么下标4的下一个位置应该指向下标0的位置。
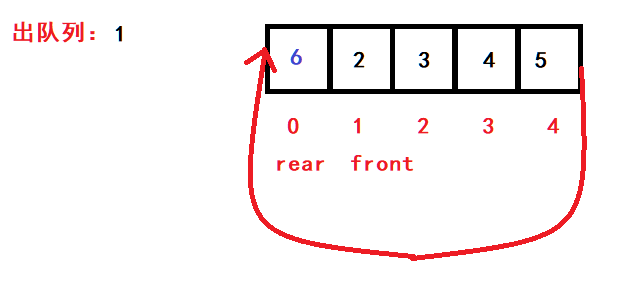
此时可以使用数组模拟实现队列,该队列为循环队列。
循环队列:
实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。
循环队列是一种基于数组实现的队列数据结构,它允许在固定大小的数组中实现队列的循环使用。循环队列解决了普通队列在出队操作后无法再次利用已出队元素的问题,通过循环利用数组空间,提高了队列的利用率。循环队列通常包含两个指针,一个指向队列的头部(front),一个指向队列的尾部(rear)。当队列满时,rear 指针会绕回到数组的起始位置,实现数组空间的循环使用。这种设计使得循环队列的入队和出队操作的时间复杂度都为 O(1)
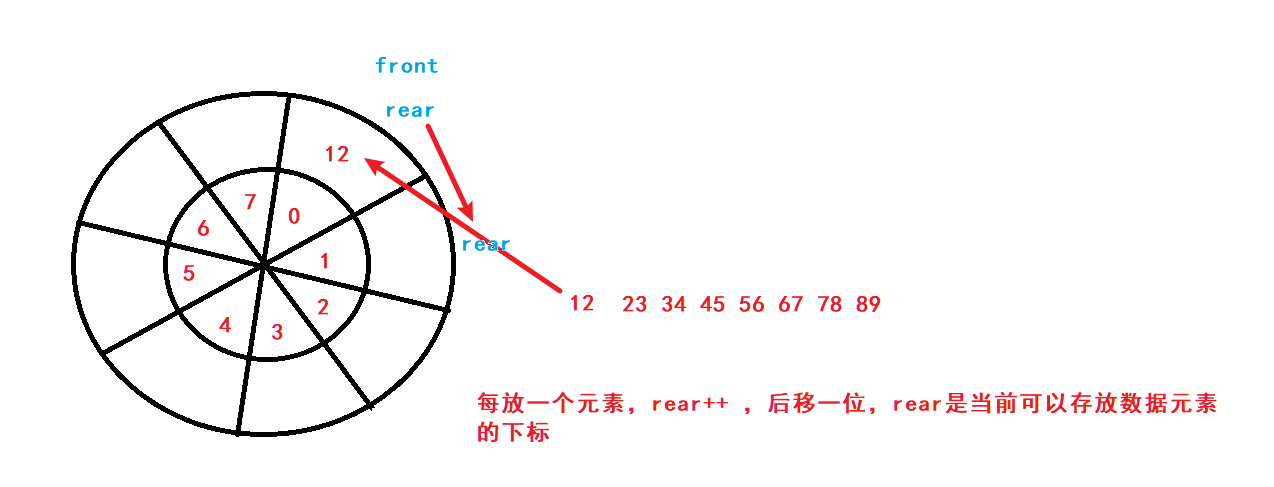
rear是当前可以存放数据元素的下标。
计算队列存储数据和删除数据的位置下标
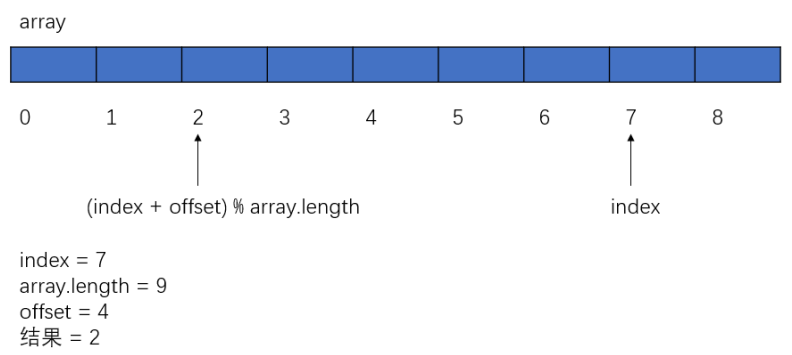
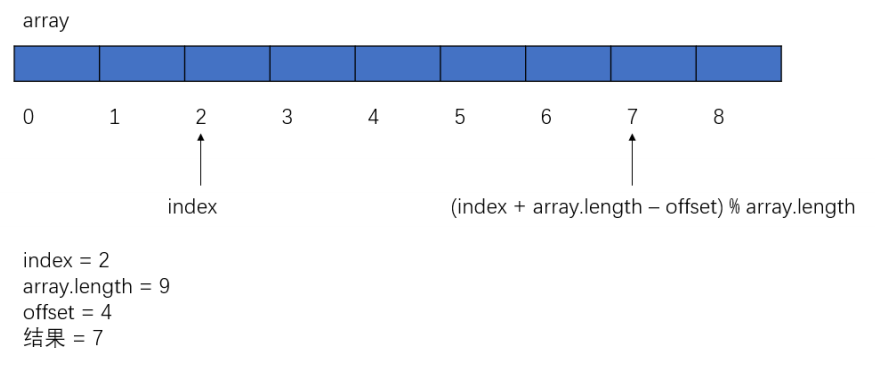
数组下标循环的小技巧
- 下标最后再往后(offset 小于 array.length): index = (index + offset) % array.length
2. 下标最前再往前(offset 小于 array.length): index = (index + array.length - offset) % array.length
如果在循环队列中存储下一个元素,数据元素存储的位置rear = (rear+1)%array.length
如果在循环队列中删除下一个元素,数据元素存储的位置front =(front+1)%array.length
区分空与满
-
通过添加 size 属性记录,当size等于数组长度时,队列是满的
-
保留一个位置,来表示满(会浪费一个空间的位置,浪费的这个空间不放元素)
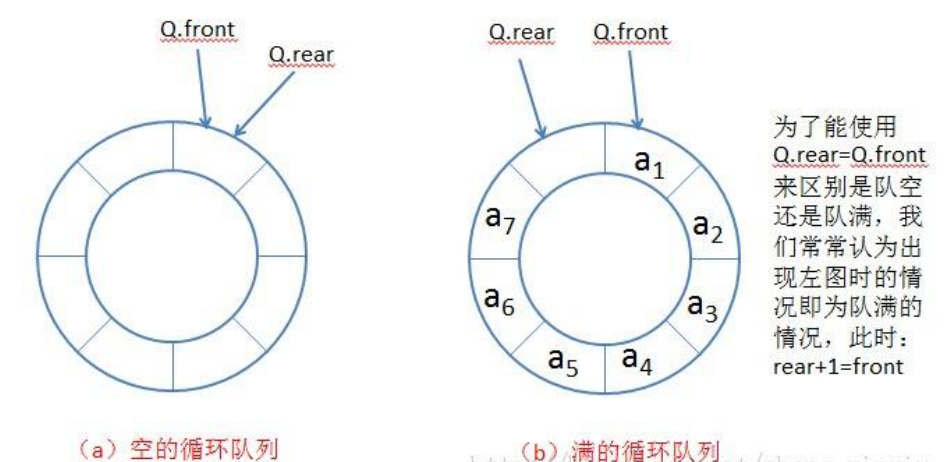
如果rear = front那么队列就是空的
如果rear的下一个元素为front,即为(rear+1)%array.length = front,那么队列就是满的。 -
使用标记
4.1 循环队列模拟实现
【题目链接】:622. 设计循环队列
class MyCircularQueue {
public int[] elem;
public int front;
public int rear;
public MyCircularQueue(int k) {
elem = new int[k + 1];
}
public boolean enQueue(int value) {
if (isFull()) {
return false;
}
elem[rear] = value;
rear = (rear + 1) % elem.length;
return true;
}
public boolean deQueue() {
if (isEmpty()) {
return false;
}
front = (front + 1) % elem.length;
return true;
}
public int Front() {
if (isEmpty()) {
return -1;
}
return elem[front];
}
public int Rear() {
if (isEmpty()) {
return -1;
}
int index = (rear == 0) ? elem.length - 1 : rear - 1;
return elem[index];
}
public boolean isEmpty() {
if (rear == front) {
return true;
}
return false;
}
public boolean isFull() {
return (rear + 1) % elem.length == front;
}
}
5. 双端队列 (Deque)
双端队列(deque,全称double-ended queue)是一种具有队列和栈的特性的数据结构。双端队列允许从两端添加和删除元素,因此可以在队列的两端进行插入和删除操作。
双端队列可以在队列的两端进行以下操作:
- 从队列的前端删除元素(出队操作)
- 从队列的前端添加元素(入队操作)
- 从队列的后端删除元素
- 从队列的后端添加元素
双端队列可以用数组或链表实现。使用双端队列可以有效地处理需要在队列两端进行操作的问题,例如实现一个双端队列可以用来实现一个双端搜索算法。
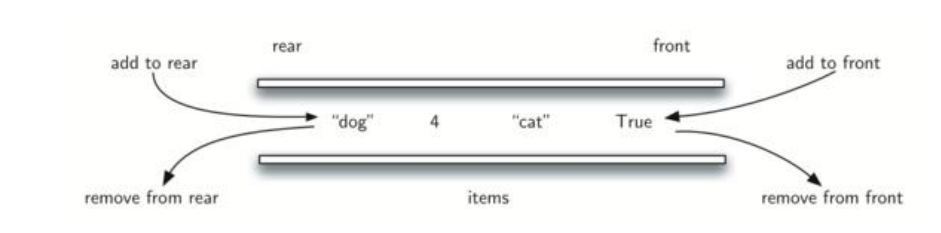
Deque是一个接口,使用时必须创建LinkedList的对象。
在实际工程中,使用Deque接口是比较多的,栈和队列均可以使用该接口。
Deque<Integer> stack = new ArrayDeque<>();//双端队列的线性实现
Deque<Integer> queue = new LinkedList<>();//双端队列的链式实现
6 用队列实现栈
【题目链接】:
225. 用队列实现栈
【题目描述】:
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素。
- int top() 返回栈顶元素。
- boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
【解题】:
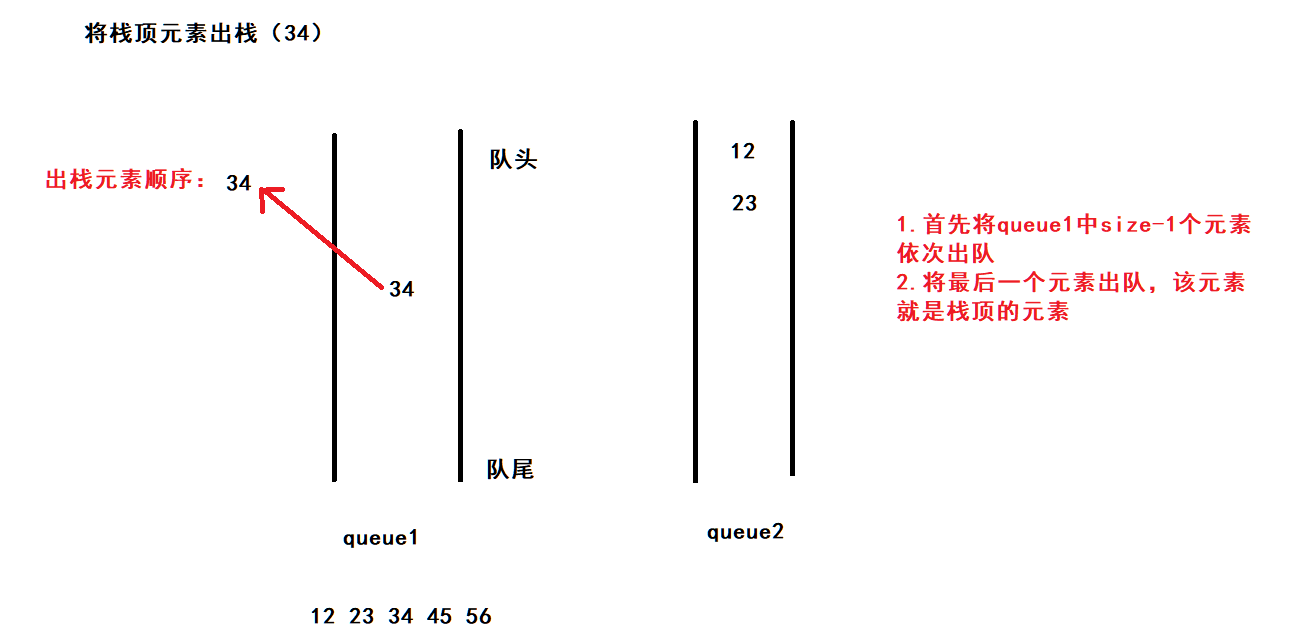
入栈:将元素放入到不为空的队列中
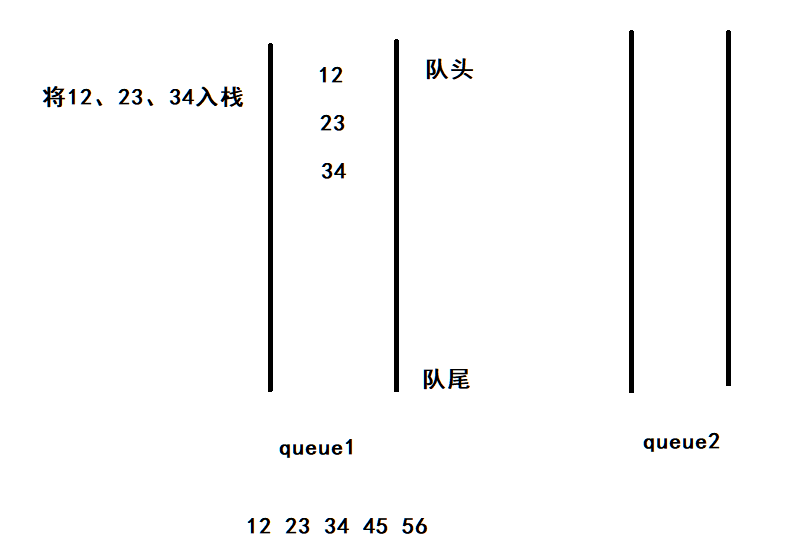
出栈:
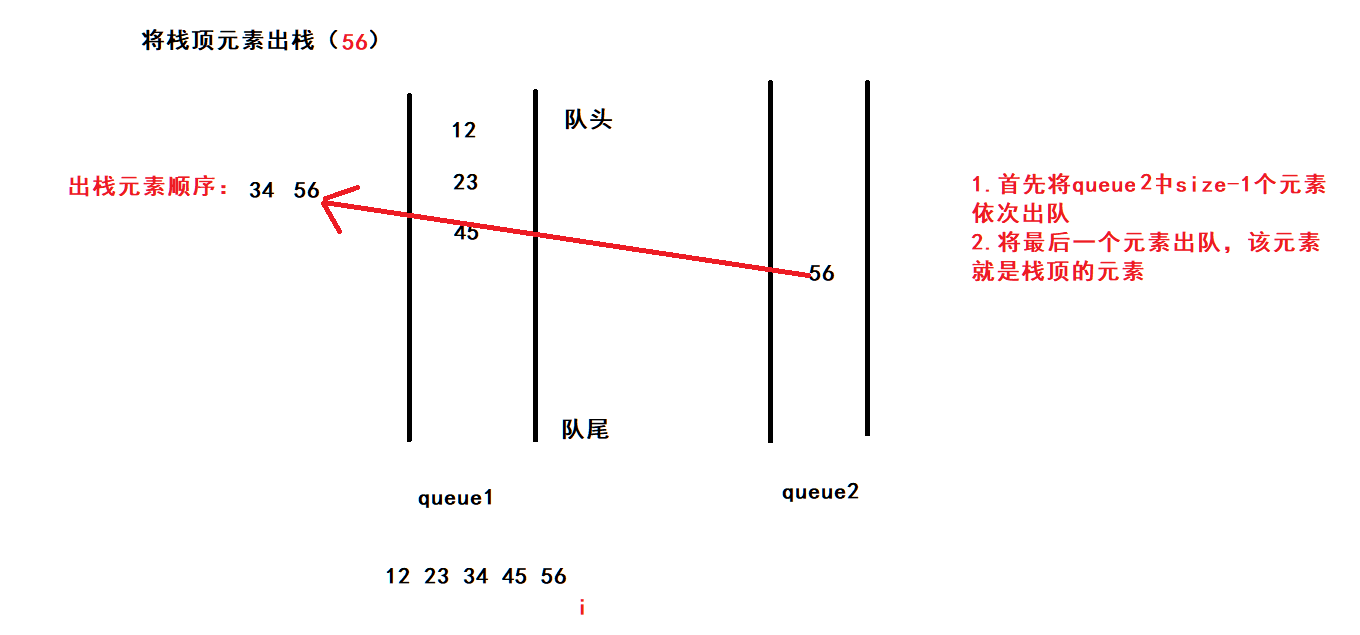
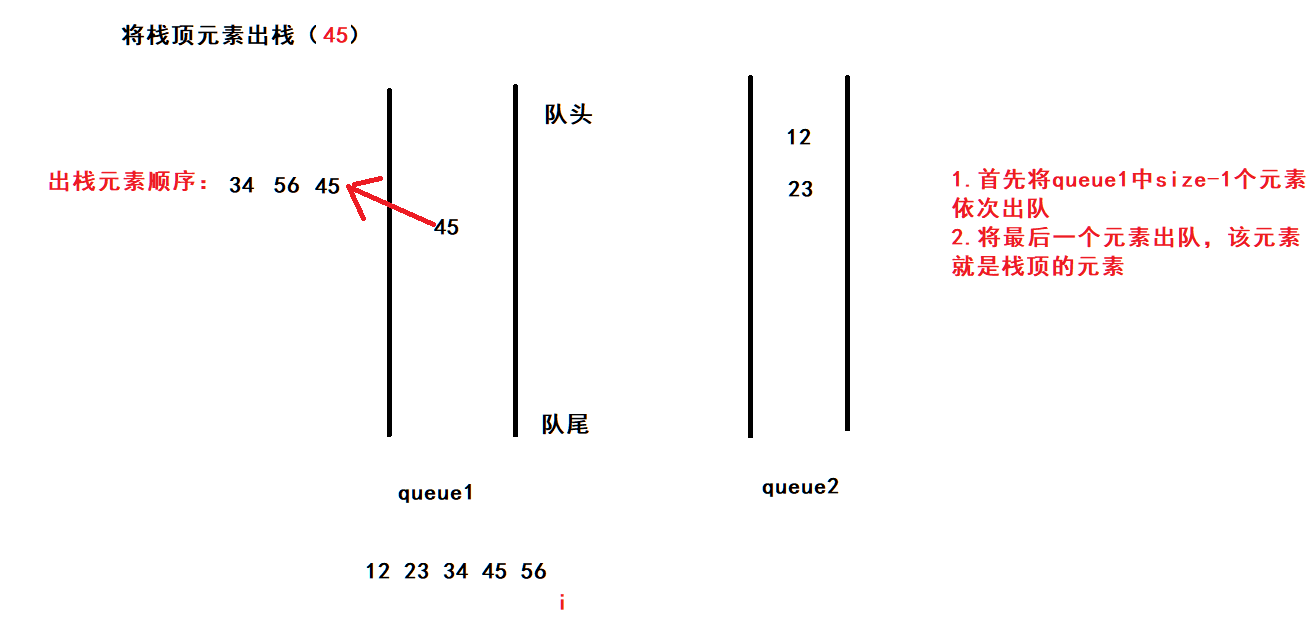
1.首先将不为空的队列中size-1个元素依次出队
2.将最后一个元素出队,该元素就是栈顶的元素
3. 重复1-2步骤,进行出栈
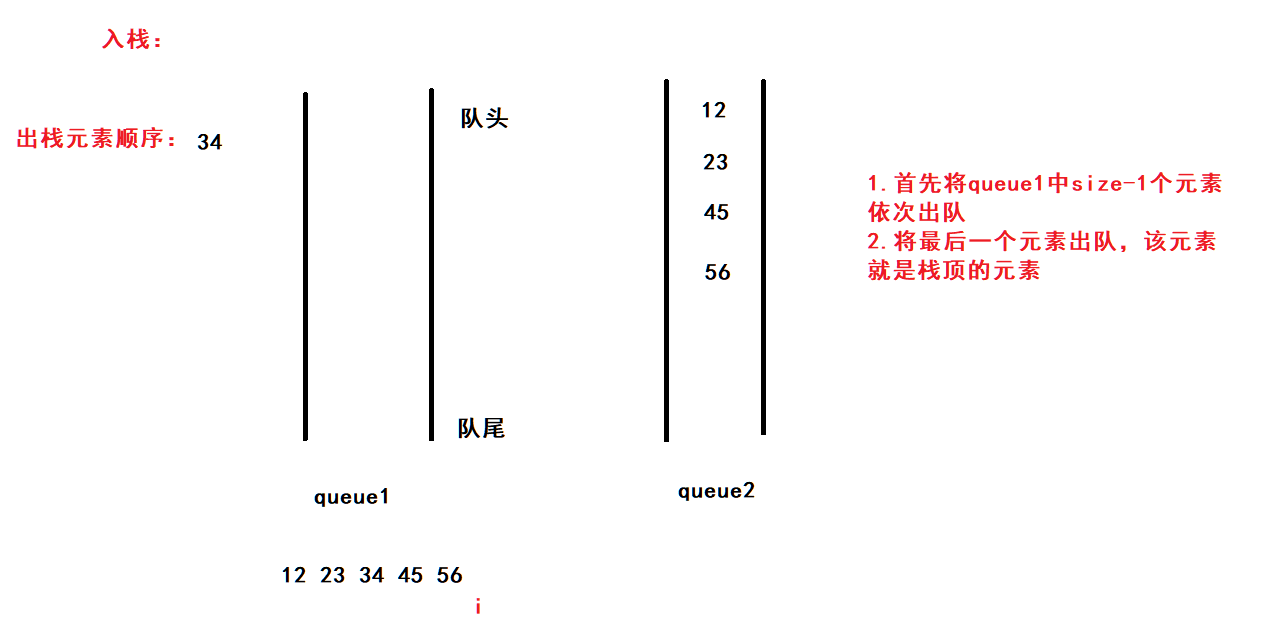
后续操作:
将45、56入栈,由于queue2不为空,将45、56放入到queue2中
出栈(56):
出栈(45):
出栈(23):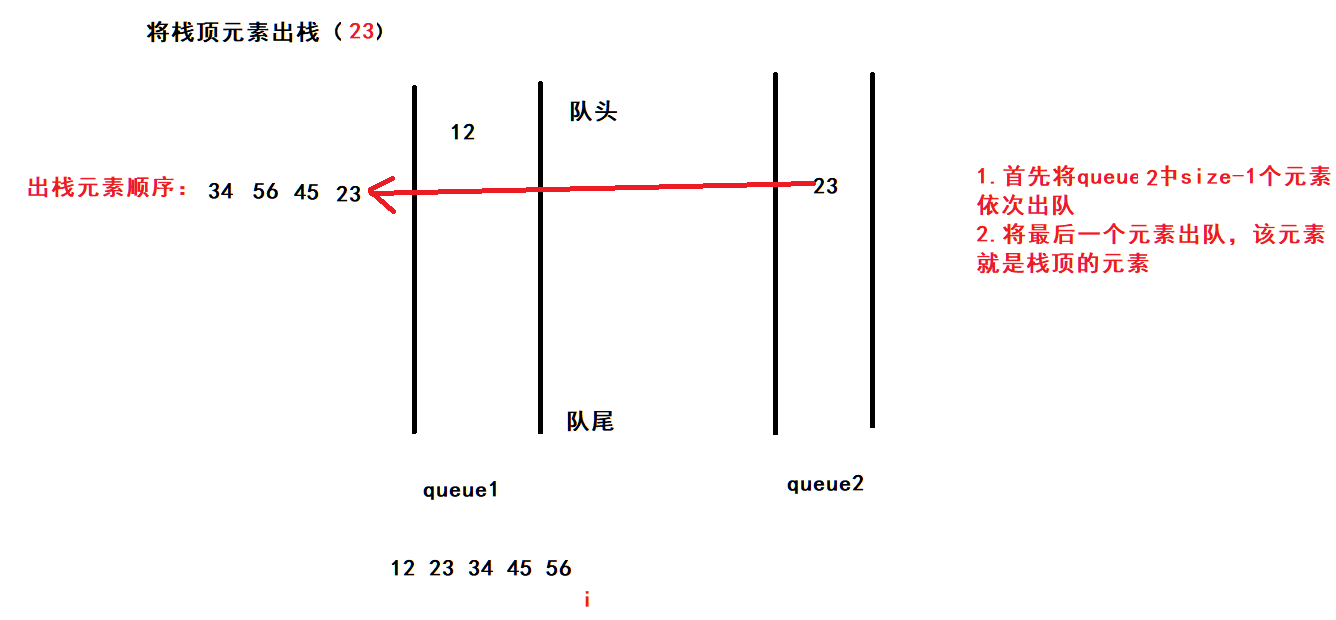
出栈(12):
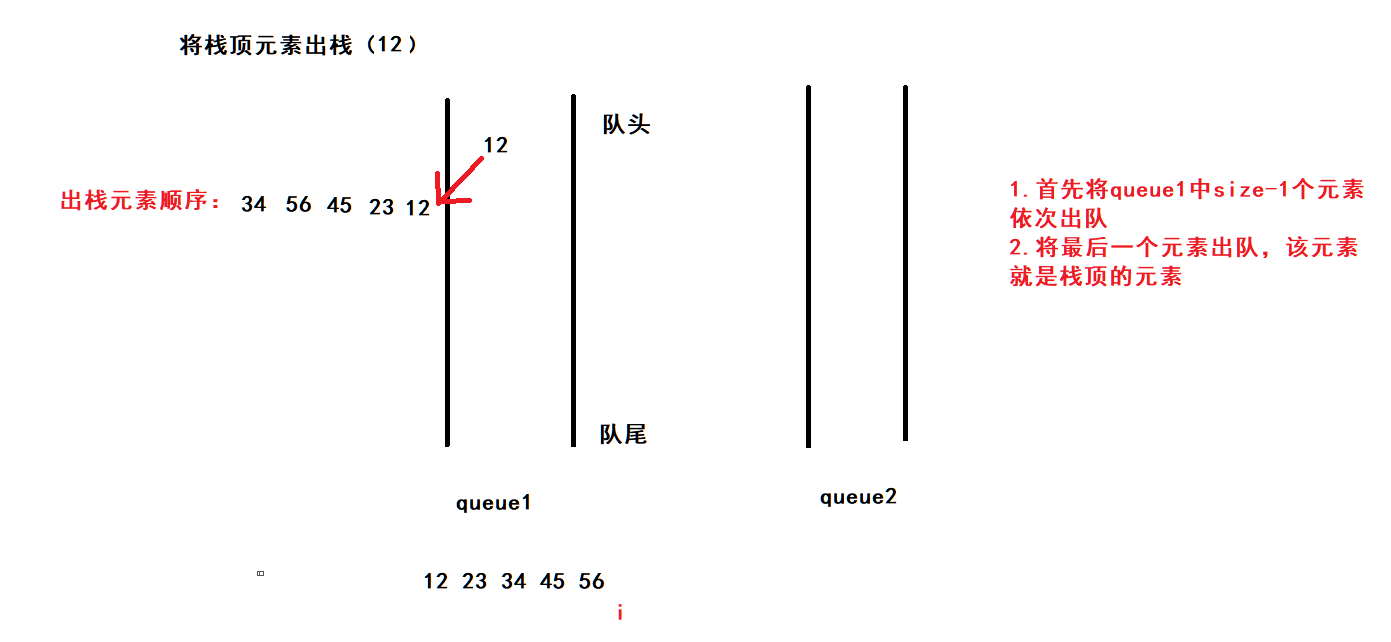
当两个队列都为空时,说明模拟的栈是空的
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new ArrayDeque<>();
queue2 = new ArrayDeque<>();
}
public void push(int x) {
if (!queue1.isEmpty()) {
queue1.offer(x);
} else if (!queue2.isEmpty()) {
queue2.offer(x);
} else {
queue1.offer(x);
}
}
public int pop() {
if (empty()) {
return -1;
}
int x = -1;
if (!queue1.isEmpty()) {
int size = queue1.size();
for (int i = 0; i < size - 1; i++) {
x = queue1.poll();
queue2.offer(x);
}
x = queue1.poll();
} else if (!queue2.isEmpty()) {
int size = queue2.size();
for (int i = 0; i < size - 1; i++) {
x = queue2.poll();
queue1.offer(x);
}
x = queue2.poll();
}
return x;
}
public int top() {
if (empty()) {
return -1;
}
int x = -1;
if (!queue1.isEmpty()) {
int size = queue1.size();
for (int i = 0; i < size; i++) {
x = queue1.poll();
queue2.offer(x);
}
} else if (!queue2.isEmpty()) {
int size = queue2.size();
for (int i = 0; i < size; i++) {
x = queue2.poll();
queue1.offer(x);
}
}
return x;
}
public boolean empty() {
return (queue1.isEmpty() && queue2.isEmpty());
}
}
7 用栈实现队列
【题目链接】:
225. 用队列实现栈
【题目描述】:
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
- void push(int x) 将元素 x 推到队列的末尾
- int pop() 从队列的开头移除并返回元素
- int peek() 返回队列开头的元素
- boolean empty() 如果队列为空,返回 true ;否则,返回 false
【解题】:
思路:借用辅助栈来实现,入队时将所有入队的元素放入辅助栈(stack1),出队时如果栈(stack2)不为空,那么就从栈(stack2)中读取数据,如果栈(stack2)为空,将辅助栈(stack1)中所有数据颠倒放入栈(stack2)中,再从栈(stack2)中读取数据。
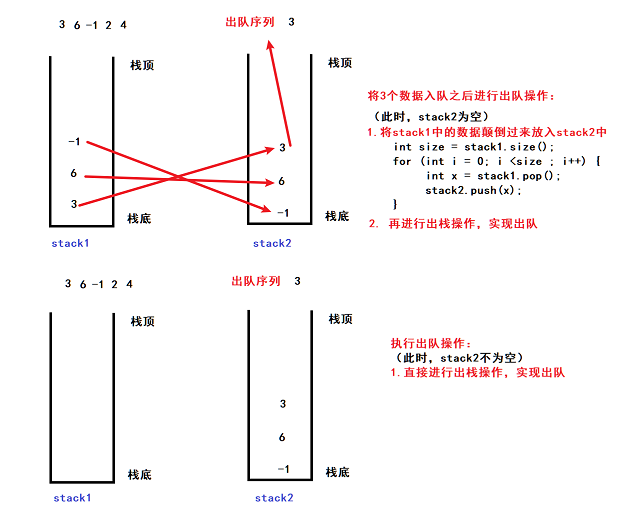
class MyQueue {
Stack<Integer> stack1;
Stack<Integer> stack2;
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void push(int x) {
stack1.push(x);
}
public int pop() {
if (empty()) {
return -1;
}
if (!stack2.empty()) {
return stack2.pop();
} else {
int size = stack1.size();
for (int i = 0; i < size; i++) {
int x = stack1.pop();
stack2.push(x);
}
return stack2.pop();
}
}
public int peek() {
if (empty()) {
return -1;
}
if (!stack2.empty()) {
return stack2.peek();
} else {
int size = stack1.size();
for (int i = 0; i < size; i++) {
int x = stack1.pop();
stack2.push(x);
}
return stack2.peek();
}
}
public boolean empty() {
return stack1.empty() && stack2.empty();
}
}