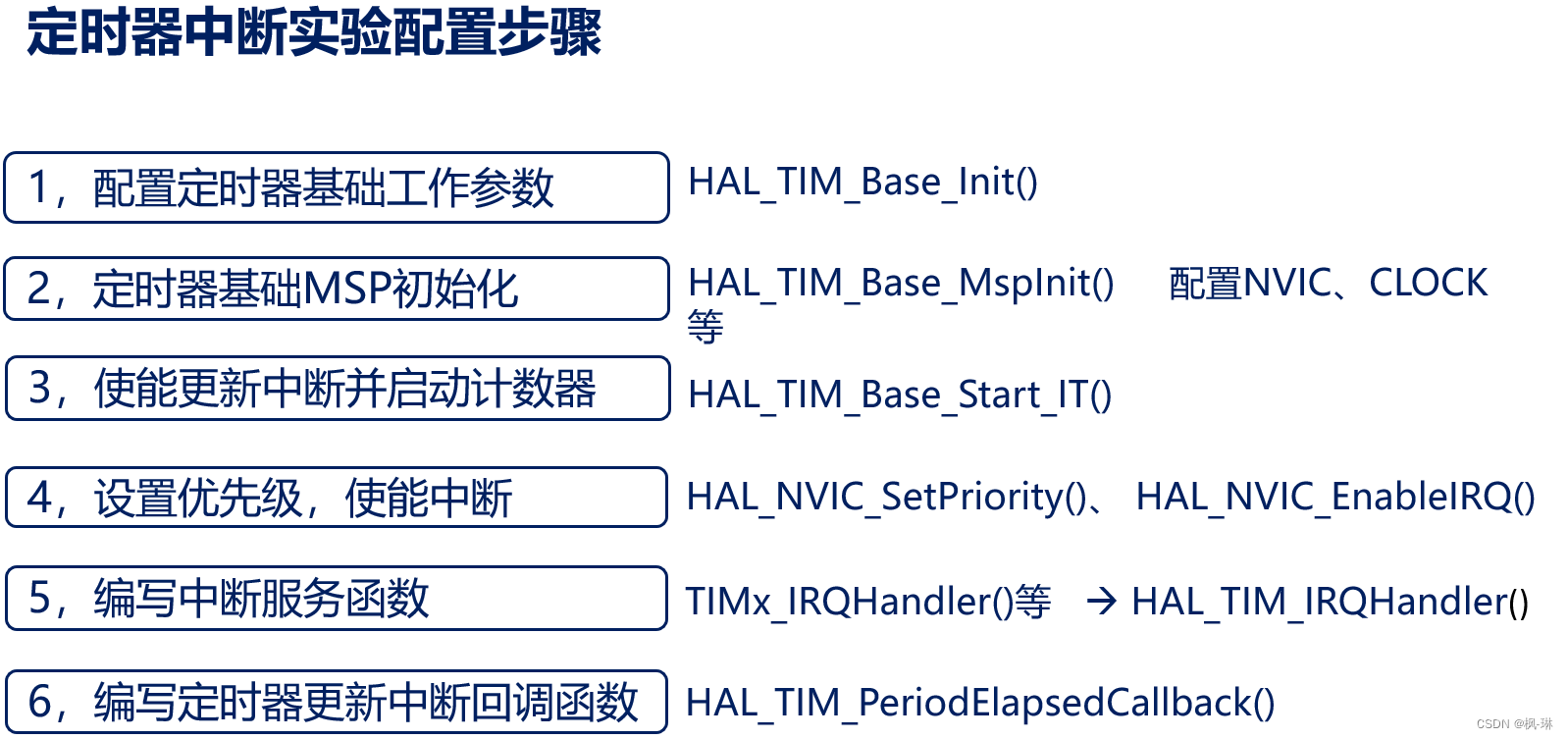
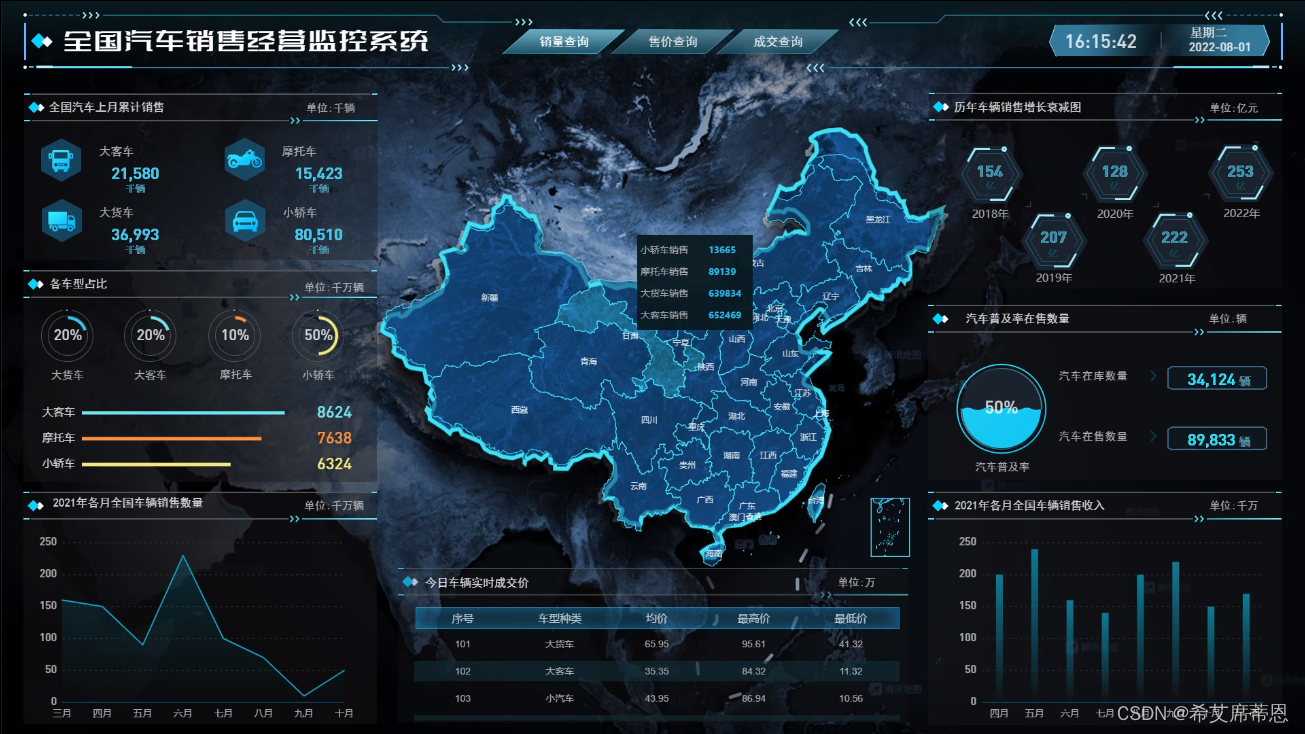
1686. 石子游戏 VI

题目描述：

Alice 和 Bob 轮流玩一个游戏，Alice 先手。

一堆石子里总共有 n 个石子，轮到某个玩家时，他可以 移出 一个石子并得到这个石子的价值。Alice 和 Bob 对石子价值有 不一样的的评判标准 。双方都知道对方的评判标准。

给你两个长度为 n 的整数数组 aliceValues 和 bobValues 。aliceValues[i] 和 bobValues[i] 分别表示 Alice 和 Bob 认为第 i 个石子的价值。

所有石子都被取完后，得分较高的人为胜者。如果两个玩家得分相同，那么为平局。两位玩家都会采用 最优策略 进行游戏。

请你推断游戏的结果，用如下的方式表示：

• 如果 Alice 赢，返回 1 。
• 如果 Bob 赢，返回 -1 。
• 如果游戏平局，返回 0 。

示例 1：

输入：aliceValues = [1,3], bobValues = [2,1]
输出：1
解释：
如果 Alice 拿石子 1 （下标从 0开始），那么 Alice 可以得到 3 分。
Bob 只能选择石子 0 ，得到 2 分。
Alice 获胜。

示例 2：

输入：aliceValues = [1,2], bobValues = [3,1]
输出：0
解释：
Alice 拿石子 0 ， Bob 拿石子 1 ，他们得分都为 1 分。
打平。

示例 3：

输入：aliceValues = [2,4,3], bobValues = [1,6,7]
输出：-1
解释：
不管 Alice 怎么操作，Bob 都可以得到比 Alice 更高的得分。
比方说，Alice 拿石子 1 ，Bob 拿石子 2 ， Alice 拿石子 0 ，Alice 会得到 6 分而 Bob 得分为 7 分。
Bob 会获胜。

提示：

• n == aliceValues.length == bobValues.length
• 1 <= n <= 10^5
• 1 <= aliceValues[i], bobValues[i] <= 100

思路：

因为两个玩家都会按照最有策略，那必然选择自己当前最大的那个呀，因此先排序，然后从后往前遍历比大小，计算两位玩家得分，最终根据得分大小返回。（有误！不一定，因为双方知晓对方的价值，如果出现田忌赛马，就有可能尽管对位没优势，但仍然获胜）

！！！上一段理解错误了，实际上只有n个石头，如果一方拿了某一石头，另一方就拿不到当前位置的石头了！！！而且，奇数个的情况下，先拿的Alice可以先拿一个！！！

事实上：

代码：

class Solution:
    def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:
        values = [[a+b, a, b] for a, b in zip(aliceValues, bobValues)]
        values.sort(reverse=True)
        aliceSum, bobSum = sum(value[1] for value in values[::2]), sum(value[2] for value in values[1::2])
        if aliceSum > bobSum:
            return 1
        elif aliceSum == bobSum:
            return 0
        else:
            return -1