2024美赛B题 (完整版在文末)
Maritime Cruises Mini-Submarines (MCMS)是一家总部位于希腊的公司,专门制造能够携 带人类到达海洋最深处的潜水艇。潜水艇是由一艘主船运输和支持的,可以在水下自由 活动。MCMS 现在希望利用他们的潜水艇带游客探索爱奥尼亚海底的沉船。然而,在此 之前,他们需要通过制定安全程序来赢得监管机构的批准,以应对与主船失去通讯和可 能发生的机械故障(包括潜水艇推进力丧失)的情况。特别地,他们希望你开发一个模 型来预测潜水艇随时间的位置
。与陆地或海面上的典型搜救不同,故障的潜水艇可能会位于海底或水下某个中性浮力 的位置。它的位置还可能受到海流、海水密度差异和/或海底地形的影响。
你的任务是:
. 定位 - 开发一个或多个模型来预测潜水艇随时间的位置。
. 这些预测有哪些不确定性?
. 潜水艇在发生事故之前可以定期向主船发送哪些信息来减少这些不确定性?潜水艇需要哪 些设备才能做到这一点?
. 准备 - 你建议公司在主船上携带哪些额外的搜救设备以备必要时使用?
. 你可以考虑不同类型的设备,但也必须考虑这些设备的可用性、维护、准备和使用成本。如 果需要,救援船需要带来哪些额外的设备来协助?
. 搜寻 - 开发一个模型,利用你的位置模型的信息,来推荐初始部署点和搜寻模式, 以便最 小化找到失踪潜水艇的时间。确定随时间和累积搜寻结果而变化的找到潜水艇的概率。
. 推广 - 你的模型如何扩展到其他旅游目的地,如加勒比海?当有多艘潜水艇在同一区域活 动时,你的模型如何改变?
. 潜水艇:潜水艇是一种水下车辆,需要由更大的水上船只或平台运输和支持。这区别于潜艇, 潜艇是自我支持的,能够在海上进行长时间的独立操作。
. 中性浮力:是指一个物体的平均密度等于它所浸没的流体的密度,导致浮力平衡了重力(如 果物体的密度大于它所浸没的流体的密度,物体就会下沉;如果小于,物体就会上升)。具 有中性浮力的物体既不会下沉也不会上升。

问题重述:
题目背景:一家希腊公司想要利用他们的潜水艇带游客探索爱奥尼亚海底的沉船,但是 需要通过监管机构的审批,制定安全程序,应对潜水艇失去通讯或动力的情况。
题目要求:建立一个模型,预测潜水艇在水中的位置随时间的变化,考虑到潜水艇可能 在海底或中层,受到海流、海水密度和海底地形的影响。同时,提出以下建议:
. 潜水艇应该定期向主船发送什么信息,以减少预测的不确定性,需要什么设备?
. 公司应该在主船上携带什么额外的搜索设备,以备不时之需?考虑到设备的成本、维护、准 备和使用。
. 建立一个模型,利用位置模型的信息,推荐初始部署点和搜索模式,以最小化定位失去的潜 水艇的时间。确定随时间和搜索结果累积而变化的找到潜水艇的概率。
. 说明如何将模型扩展到其他旅游目的地,如加勒比海。说明如何修改模型,以适应同一区域 内多艘潜水艇的移动。
这个题目的重点难点有以下几个方面:
. 如何建立一个能够准确预测潜水艇在水中位置的模型,考虑到潜水艇可能在海底或中层,受 到海流、海水密度和海底地形的影响。
. 如何评估模型的不确定性,以及潜水艇应该定期向主船发送什么信息,以减少不确定性,需 要什么设备。
. 如何在主船上准备合适的搜索设备,以应对潜水艇失去通讯或动力的情况,考虑到设备的成 本、维护、准备和使用等因素。
. 如何利用位置模型的信息,推荐最佳的初始部署点和搜索模式,以最小化搜索和定位潜水艇 所需的时间, 以及计算找到潜水艇的概率。
. 如何将模型扩展到其他海域,如加勒比海,以及如何调整模型,以适应同一海域内有多艘潜 水艇同时运行的情况。
为了解决这些问题,我认为可能需要应用以下几种数学模型:
. 位置预测模型:可以考虑使用微分方程模型,将潜水艇的位置、速度、方向、深度等作为状 态变量,将海流、海水密度、海底地形等作为影响因素,建立一个动态系统,描述潜水艇的 运动规律。也可以考虑使用机器学习模型,如神经网络、支持向量机等,利用历史数据或模 拟数据,训练一个能够根据潜水艇的初始状态和环境条件,预测其未来位置的模型。
. 不确定性评估模型:可以考虑使用概率统计模型,如置信区间、假设检验、蒙特卡罗模拟等, 分析位置预测模型的误差、稳定性、灵敏度等,评估模型的可靠性和有效性。也可以考虑使 用信息论模型,如熵、互信息、信息增益等,分析潜水艇向主船发送的信息的质量和量化, 确定最优的通讯和定位设备和策略。
. 搜索设备选择模型:可以考虑使用多目标规划模型,将搜索设备的成本、维护、准备、使用 等作为目标函数,将搜索设备的类型、数量、性能等作为决策变量,将搜索设备的可用性、 安全性、兼容性等作为约束条件,建立一个优化问题,求解最优的搜索设备组合和配置方案。
. 搜索模式推荐模型:可以考虑使用图论模型,将海域划分为若干个网格,将每个网格作为一 个节点,将节点之间的距离作为边的权重,建立一个加权图,描述海域的空间结构。然后可 以考虑使用最短路径算法、最小生成树算法、最小费用最大流算法等,根据位置预测模型的 信息,推荐最佳的初始部署点和搜@b 站珞珈山水 1 q 群 476179473 索模式, 以最小化搜索 和定位潜水艇所需的时间。也可以考虑使用概率模型,如马尔可夫链、贝叶斯网络等,根据 位置预测模型的信息,计算每个网格中找到潜水艇的概率,以及随时间和搜索结果累积而变 化的找到潜水艇的概率。
. 模型扩展和调整模型:可以考虑使用灵敏度分析模型,分析模型对不同海域的海流、海水密 度、海底地形等参数的敏感性,确定模型的适用范围和可推广性。也可以考虑使用博弈论模 型,分析多艘潜水艇在同一海域内的相互影响和协作策略,确定模型的修改和优化方案。
1. 潜水器动力系统失效:模型需要考虑潜水器在无推进力情况下的行为。
2. 失去与主船通信:考虑无法从主船接收指令或发送位置信息的情况。
3. 中性浮力和海底定位:潜水器可能位于海底或达到水下某个中性浮力点。 4. 水流和海水密度变化:影响潜水器位置的环境因素。
5. 海底地理:海底的地形可能会影响潜水器的最终位置或移动路径。
数学模型和公式
为预测潜水器的位置,我们可以建立基于物理学原理的动态模型,考虑力学和流体动力 学的因素。以下是潜水器运动的基本方程:@b 站珞珈山水 1 q 群 476179473
动力学方程
设潜水器的质量为 mm ,受到的浮力为 FbF_b ,重力为 FgF_g ,水流对潜水器施加 的力为 FcF_c ,潜水器在水中的阻力为 F_d ,则潜水器的运动方程可表示为:
md2r→dt2=Fb→+Fg→+Fc→− Fd→ m\frac{d^2\vec{r}}{dt^2} = \vec{F_b} + \vec{F_g} + \vec{F_c} - \vec{F_d}
其中, r →\vec{r} 是潜水器的位置向量, tt 是时间。
mm :潜水器的质量
Fb→\vec{F_b} :浮力,方向向上
Fg→=m ⋅ g\vec{F_g} = m \cdot g :重力,方向向下, gg 是重力加速度
Fc→\vec{F_c} :水流对潜水器的作用力,方向依赖于水流方向
Fd→\vec{F_d} :阻力,方向与潜水器运动方向相反,大小可以用 Fd=12ρv2CdAF_d =
\frac{1}{2} \rho v^2 C_d A 来估计,其中 ρ\rho 是水的密度, vv 是潜水器相对于水的速 度, CdC_d 是阻力系数,$A$ 是潜水器迎水面积
潜水器浮力和阻力的计算
浮力 FbF_b 可以通过潜水器排水量和水的密度来计算,阻力 FdF_d 可以根据潜水器的 形状、表面粗糙度和运动速度来估算。
数值解法
潜水器的运动方程是一个二阶微分方程,我们可以采 用数值方法(如欧拉方法或龙格-库塔方法)对其进行求解,得到潜水器随时间变化的 位置和速度。
模型假设
. 潜水器被视为质点,忽略其尺寸和形状的影响。
. 假设水流速度和方向是已知的,可以从海洋流动模型获得。
. 海底地形对潜水器运动的影响通过调整浮力和阻力参数来模拟。
通过上述模型和方法,我们可以预测在不同情况下潜水器的位置,为 MCMS 制定安全程 序提供科学依据。
为了解决上述复杂的数学建模问题,我们将问题分解为四个主要部分:定位、准备、搜 索和外推。下面是针对每个部分的详细分析和数学模型。
定位
模型构建
. 基于多传感器融合的动态预测模型:利用卡尔曼滤波(Kalman Filter)或扩展卡尔曼滤波 (Extended Kalman Filter, EKF)来整合来自潜水器内部(如 IMU 传感器)和外部(如声纳、 GPS 浮标)的多源信息,预测潜水器随时间变化的位置。
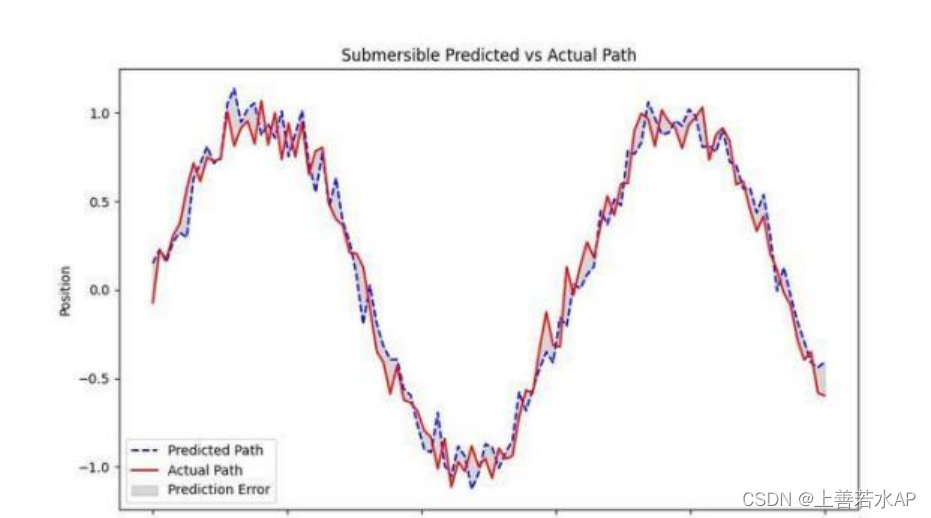
数学公式
假设潜水器的状态为 x →t= [xt,yt,zt,x˙t,y˙t,z˙t]T\vec{x}_t = [x_t, y_t, z_t, \dot{x}_t, \dot{y}_t, \dot{z}_t]^T ,
其中 xt,yt,ztx_t, y_t, z_t 表示潜水器在三维空间中的位置,
x˙t,y˙t,z˙t\dot{x}_t, \dot{y}_t, \dot{z}_t 表示对应的速度。
卡尔曼滤波的预测和更新步骤如下:
. 预测步骤: x →t |t− 1=F →tx→t− 1 |t− 1+B→tu→t \vec{x}_{t |t- 1} = \vec{F}_t \vec{x}_{t- 1 |t- 1} + \vec{B}_t \vec{u}_t P →t |t− 1=F →tP→t− 1 |t− 1F→tT+Q→t \vec{P}_{t |t- 1} = \vec{F}_t \vec{P}_{t- 1 |t- 1} \vec{F}_t^T + \vec{Q}_t
. 更新步骤: K →t=P →t |t− 1H→tT(H→tP→t |t− 1H→tT+R→t)−1 \vec{K}_t = \vec{P}_{t|t- 1} \vec{H}_t^T (\vec{H}_t \vec{P}_{t |t- 1} \vec{H}_t^T + \vec{R}_t)^{- 1} x →t |t=x →t |t− 1+K→t(z →t− H →tx→t |t− 1) \vec{x}_{t |t} = \vec{x}_{t |t- 1} + \vec{K}_t (\vec{z}_t - \vec{H}_t \vec{x}_{t |t- 1}) P→t |t=(I− K →tH→t)P→t |t− 1 \vec{P}_{t |t} = (I - \vec{K}_t \vec{H}_t) \vec{P}_{t |t- 1}
其中, F →t\vec{F}_t 是状态转移矩阵, B →t\vec{B}_t 是控制输入矩阵, u →t\vec{u}_t 是外部控制输入,P →t\vec{P}_t 是估计误差协方差,Q→t\vec{Q}_t 是过程噪声协方差, H →t\vec{H}_t 是观测模型矩阵, R →t\vec{R}_t 是观测噪声协方差, K →t\vec{K}_t 是卡 尔曼增益, z →t\vec{z}_t 是实际观测值。
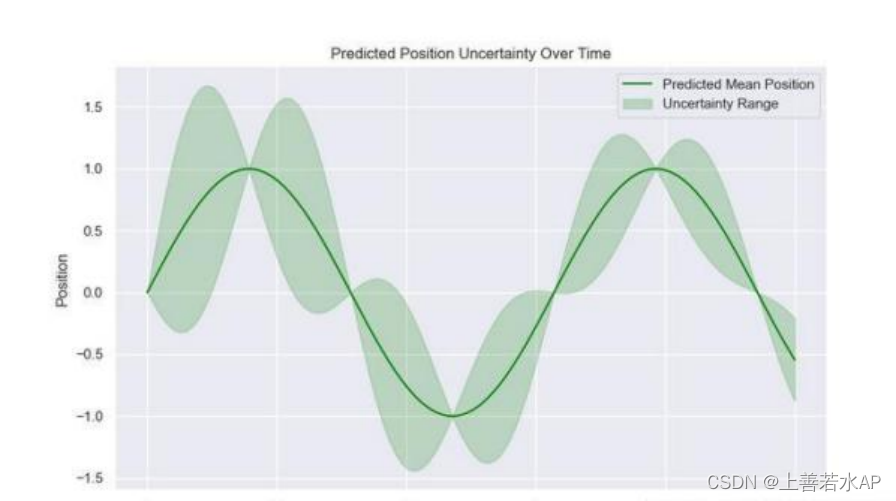
不确定性分析
. 主要的不确定性来源包括传感器噪声、模型误差、外部环境(如水流变化和海底地形)的未 知性。蒙特卡洛模拟(Monte Carlo Simulation)可用于评估这些不确定性对预测准确性的影 响。
. 附加搜索设备推荐:基于成本-效益分析,推荐搭载多波束声纳(用于精确地图制作)和侧 扫声纳(用于宽范围搜索)。
. 设备需求和成本分析:使用线性规划模型来平衡设备的可用性、维护成本、准备状态和使用 成本。
. 基于概率地图的搜索模型:结合潜水器位置预测模型和海域环境信息(如水流、海底地形), 使用贝叶斯搜索理论(Bayesian Search Theory)来确定最佳搜索区域和搜索路径,最小化找 到失联潜水器的时间。2024美赛B题详细技术文档22页+配套每小问代码+数据集汇总去+参考论文