前言

二叉树的简单题目，通过画栈帧图去理解过程。画一画，走一走递归过程，理解会更加深刻。

二叉树练习题

前言
二叉树的创建
- 二叉树先序遍历创建
- - PreCreat
- 二叉树层次创建
- - LevelCreat
二叉树的销毁
- BinaryTreeDestory
二叉树求节点个数
- BinaryTreeSize
二叉树叶子节点个数
- BinaryTreeLeafSize
二叉树求高度
- BinaryBTHeight
二叉树第k层的节点数
- BinaryTreeLevelKSize
检测两颗二叉树是否完全相同
- isSameTree
另一棵树的子树
- isSubtree
二叉树的翻转
- invertTree

二叉树的创建

二叉树先序遍历创建

根据前序遍历的序列"ABD##E#H##CF##G##"

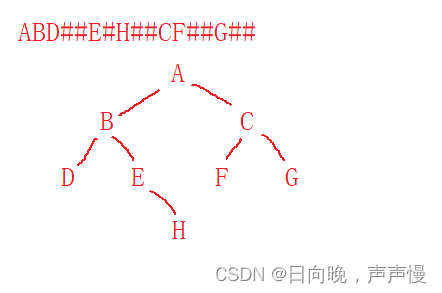
在这里插入图片描述

PreCreat

调用函数，需谨记形参的改变不能改变实参。在对字符串遍历的过程，需要确保每次栈帧中，对应下标是正确的，那么传参是必须传址调用。

看不懂的话，属实没辙，需要自己画一画。每个栈帧相当于一个节点，只有函数返回后，才能把整个树串起来。
你可以这样去理解递进过程：（看实际的二叉树）递进过程做的事情是每个节点找到了自己所在的位置。
返回过程：父子节点手拉手，心连心（皮一皮）

如何看递归展开图：跟着箭头和代码。

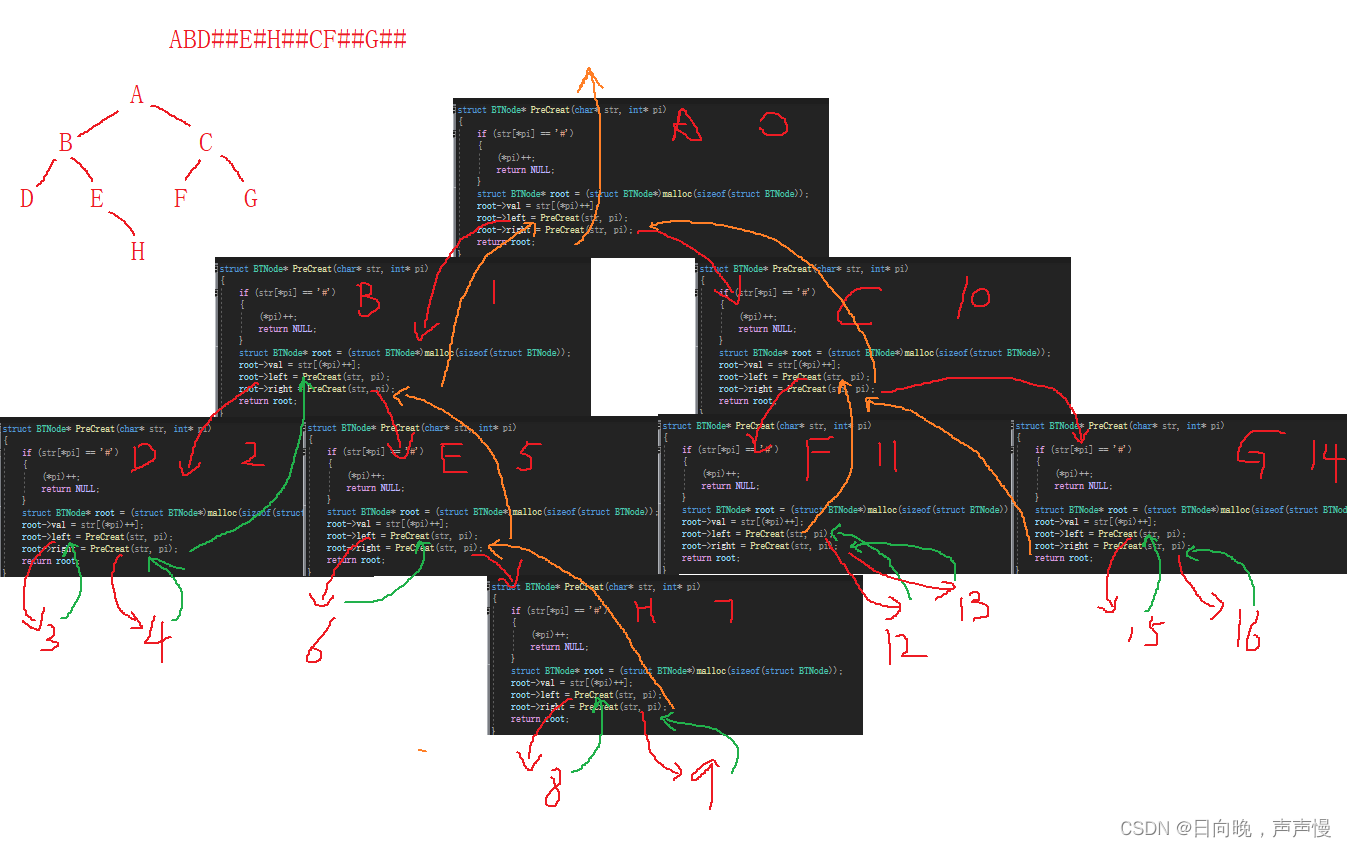
在这里插入图片描述

 struct BTNode
{
	int val;
	struct BTNode* left;
	struct BTNode* right;
};

struct BTNode* PreCreat(char* str, int* pi)
{
	if (str[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}
	struct BTNode* root = (struct BTNode*)malloc(sizeof(struct BTNode));
	root->val = str[(*pi)++];
	root->left = PreCreat(str, pi);
	root->right = PreCreat(str, pi);
	return root;
}
int main()
{
	char str[] = "ABD##E#H##CF##G##";
	int i = 0;
	struct BTNode* root = PreCreat(str, &i);
	return 0;
}

二叉树层次创建

层次创建二叉树。给定层次遍历的结果，将之变成对应的二叉树。
需要用到队列，哪个过程符合先进先出的原则呢？取父节点的过程。
层次遍历结果的字符串为：1234\0，1、2、3这三个节点很容易串起来，关键在4节点怎么找到它的父节点是2节点，假设后面还有节点，怎么保证后面的每个节点都能对应的上相应的父节点。
通过队列来保证，#表示NULL。

根节点先入队，进入循环。循环结束条件：当前字符串不为'\0'。出队的节点当作父节点，并且按顺序链接左孩子、右孩子并把这两个孩子按顺序入队。重复

在这里插入图片描述

下列代码为伪代码：未把队列的接口函数给出。栈和队列需要的话自己去这个博客里cv一下。

LevelCreat


struct BTNode
{
	char val;
	struct BTNode* left;
	struct BTNode* right;
};

typedef struct BTNode* QDataType;
// 链式结构：表示队列 
typedef struct QListNode
{
	QDataType data;
	struct QListNode* next;

}QNode;

// 队列的结构 
typedef struct Queue
{
	QNode* front;
	QNode* rear;
}Queue;

struct BTNode* AollocBTNode(char val)
{
	struct BTNode* root = (struct BTNode*)malloc(sizeof(struct BTNode));
	root->val = val;
	root->left = NULL;
	root->right = NULL;
	return root;
}
struct BTNode* LevelCreat(char* str)
{
	Queue q;
	QueueInit(&q);
	int i = 0;
	struct BTNode* root = AollocBTNode(str[i++]);
	struct BTNode* Reroot = root;

	QueuePush(&q, root);
	//1234
	while (str[i] != '\0')
	{
		root = QueueFront(&q);//取队头元素
		QueuePop(&q);//弹出队头元素
		if (str[i] != '#')
		{
			root->left = AollocBTNode(str[i++]);
			QueuePush(&q, root->left);//左孩子入队
		}
		else
			i++;
		if (str[i] != '\0')
		{
			if (str[i] != '#')
			{
				root->right = AollocBTNode(str[i++]);
				QueuePush(&q, root->right);//右孩子入队
			}
			else
				i++;
		}
	}
	QueueDestroy(&q);
	return Reroot;
}
int main()
{
	char str[] = "ABCDEFG###H";
	struct BTNode* root = LevelCreat(str);
	return 0;
}

二叉树的销毁

什么时候将空间释放？肯定是最后一次经过该节点的时候，那么得选择后序遍历。
（前序：第一次经过某个节点，中序：第二次经过某个节点，后序：最后一次经过某个节点）
不管是第一次，还是第二次经过某个节点，都不能释放，因为它递归还没执行到最后，如果先把节点释放了，它继续进行递归就会找不到它的孩子们了。
下面给了两种形式的，一个是二级指针形式，一个是一级指针形式的。
二级指针形式是传址调用，释放后对应的指针（指向每个节点的指针）都会置为NULL
一级指针形式是传值调用，释放后对应的指针仍然指向该地址，但没有权限访问。为了避免非法访问，调用完该函数后，主函数中还需要执行root = NULL;

BinaryTreeDestory

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	if (*root == NULL)
		return;
	BinaryTreeDestory(&((*root)->left));
	BinaryTreeDestory(&((*root)->right));
	free(*root);
	*root = NULL;
}
//主函数调用BTDestory后还需要执行 root = NULL;
void BTDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BTDestory(root->left);
	BTDestory(root->right);
	free(root);
}
//伪代码：
int main()
{
     BTDestory(root);
     root = NULL;
}

二叉树求节点个数

看图理解。函数中的+1这个1是当前栈帧中是否有节点

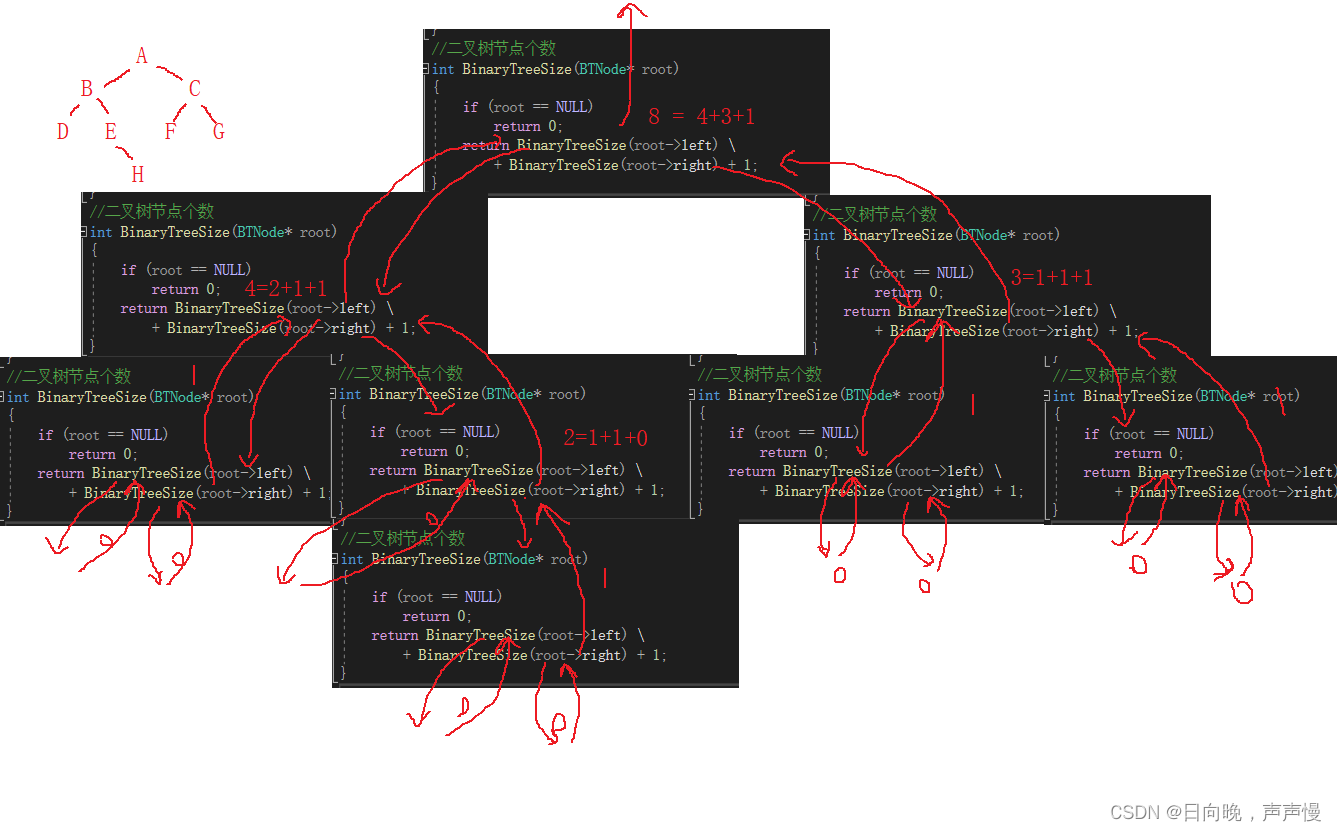
在这里插入图片描述

BinaryTreeSize

int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

二叉树叶子节点个数

通过递归去走完每一个节点，走到特定的节点（叶子节点），需要带回返回值。
和上面一题差不多。叶子节点：没有左孩子也没有右孩子的节点。
需要判断：只有是叶子节点的时候才返回1，当为NULL时返回0，其它情况返回之前的结果。
可以像我上面画的图一样，自己动手画一画，去理解其中过程。

BinaryTreeLeafSize

int BinaryTreeLeafSize(BTNode* root)
{
	if (root && root->left == NULL && root->right == NULL)
		return 1;
	if (root == NULL)
		return 0;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

二叉树求高度

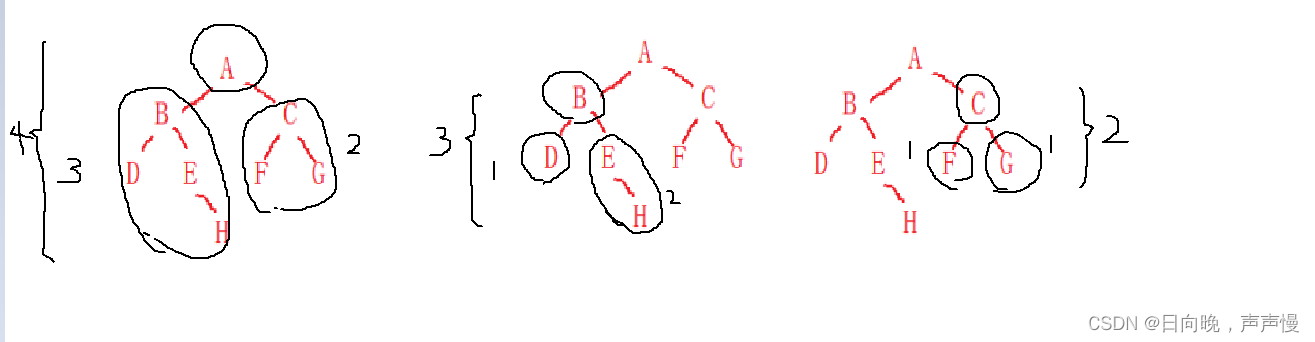
随便给你一颗树，你怎么求这个树的高度呢？
分治思想：在某节点，你知道该节点的左子树、右子树的高度，取其中最大值，再+1就能得到当前节点总共的高度。每一棵子树都是这样得到的。
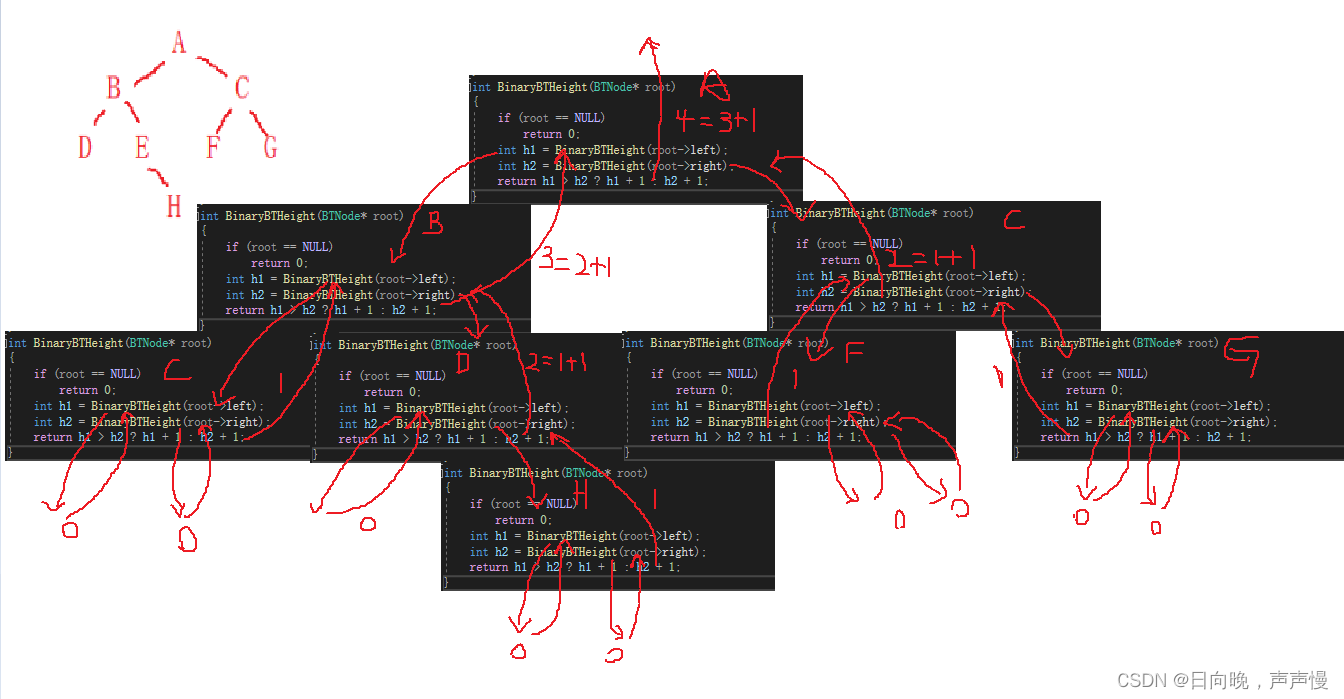
在代码具体实现的时候，是先知道最下面的高度，返回后才能知道上面节点的高度。

在这里插入图片描述

BinaryBTHeight

int BinaryBTHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int h1 = BinaryBTHeight(root->left);
	int h2 = BinaryBTHeight(root->right);
	return h1 > h2 ? h1 + 1 : h2 + 1;
}

二叉树第k层的节点数

假设k为3，根据下图所示，当k==1时，就是我们所要找的层，因此在这里就可以返回了。

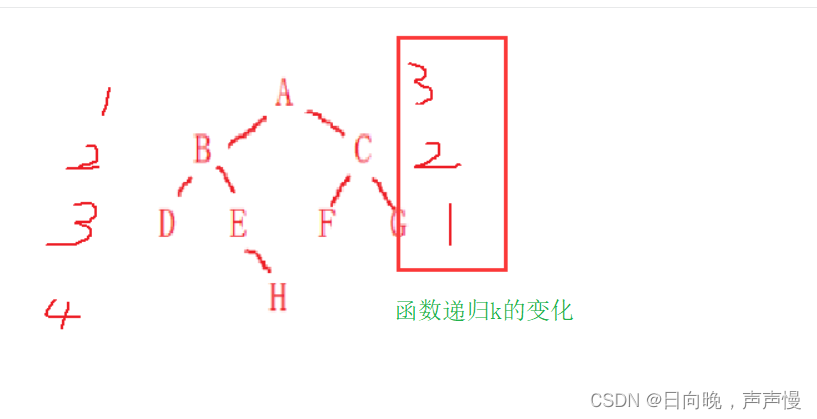
在这里插入图片描述

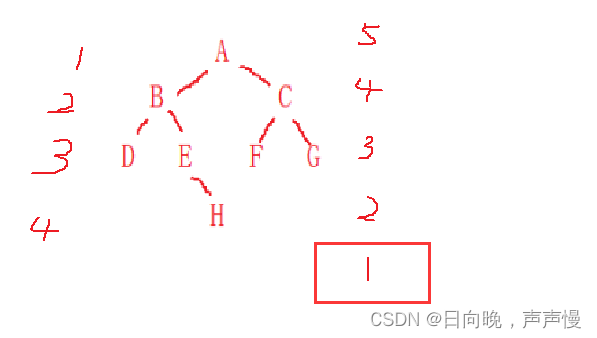
如果k为5，不会到k==1，会先碰到NULL返回

在这里插入图片描述

BinaryTreeLevelKSize

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) +
		BinaryTreeLevelKSize(root->right, k - 1);
}

检测两颗二叉树是否完全相同

LeetCode.100.相同的树

写的时候要直接写能得出结果的，就是说当两棵树不相同的时候，直接返回false，而不判断是否相同，因为当前节点相同了，但是它的孩子不一定相同。不相等时直接返回false简单粗暴。

会出现下面两种情况：①一棵树为NULL,另一棵为非空，这种情况是false。②两棵树的节点都为NULL才能说是true。条件写的时候②要放在上面，①要放在下面。因为if(p == NULL || q == NULL)这个条件包含了p == NULL && q == NULL这种情况

isSameTree

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
    return true;
    if(p == NULL || q == NULL)
    return false;
    if(p && q && p->val != q->val)
    return false;
    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

另一棵树的子树

LeetCode.572.另一棵树的子树
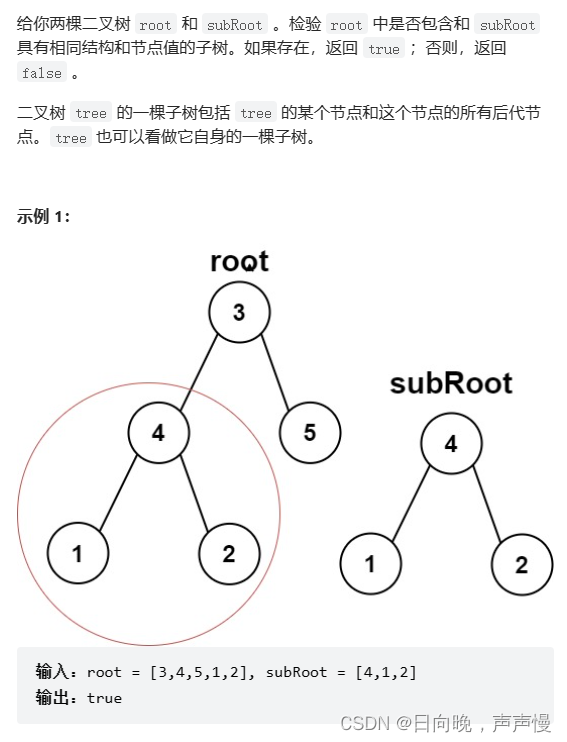
在这里插入图片描述

还记的上面一题写的相同的树吗？在这一题可以使用吗？当然可以，而且这样写会非常简单。
root这棵树去遍历它的每个节点，每个节点都当作新子树的根和subRoot这棵树判断是否为相同的树。相同了就可以返回true，这种情况下是不需要遍历完所有的节点。如果遍历完所有的节点，都没相同的子树才能说false。因此返回的逻辑关系是“或”

isSubtree

 bool isSameTree(struct TreeNode* p, struct TreeNode* q)
 {
	 if (q == NULL && p == NULL)
		 return true;
	 if (q == NULL || p == NULL)
		 return false;
	 if (q->val != p->val)
		 return false;
	 return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
 }
 bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
	 if (root == NULL)
		 return false;
	 if (isSameTree(root, subRoot))
		 return true;
	 return isSubtree(root->left, subRoot) ||isSubtree(root->right, subRoot);

}

二叉树的翻转

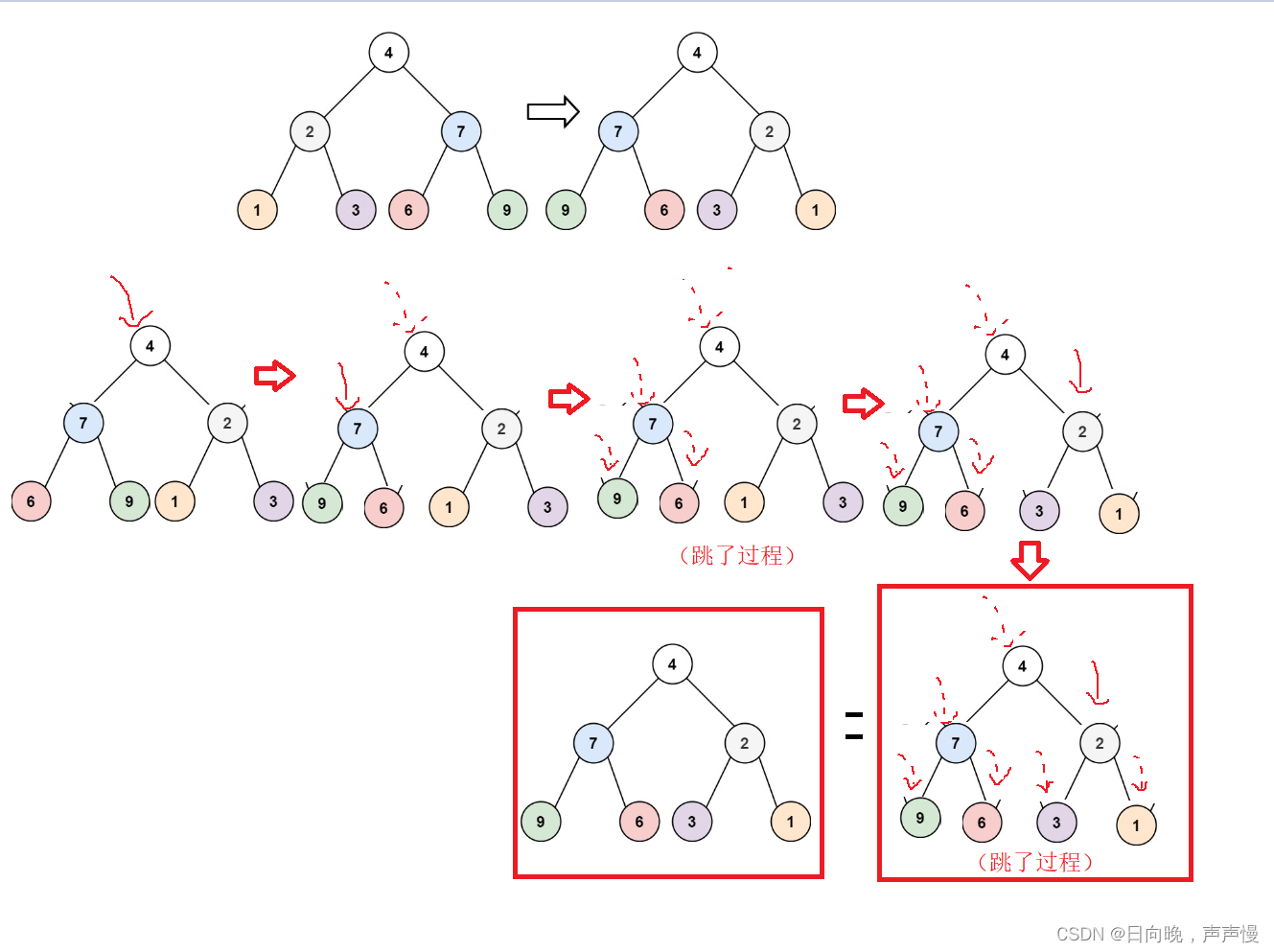
找到规律就很简单。每个节点的孩子交换，就能完成翻转。

invertTree

struct TreeNode* invertTree(struct TreeNode* root)
{
    if (root == NULL)
        return NULL;
    struct TreeNode* tmp = root->left;
    root->left = root->right;
    root->right = tmp;
    invertTree(root->left);
    invertTree(root->right);
    return root;
}