需求简述
求所有 GF(2)上 次数小于等于8 的 不可约多项式。
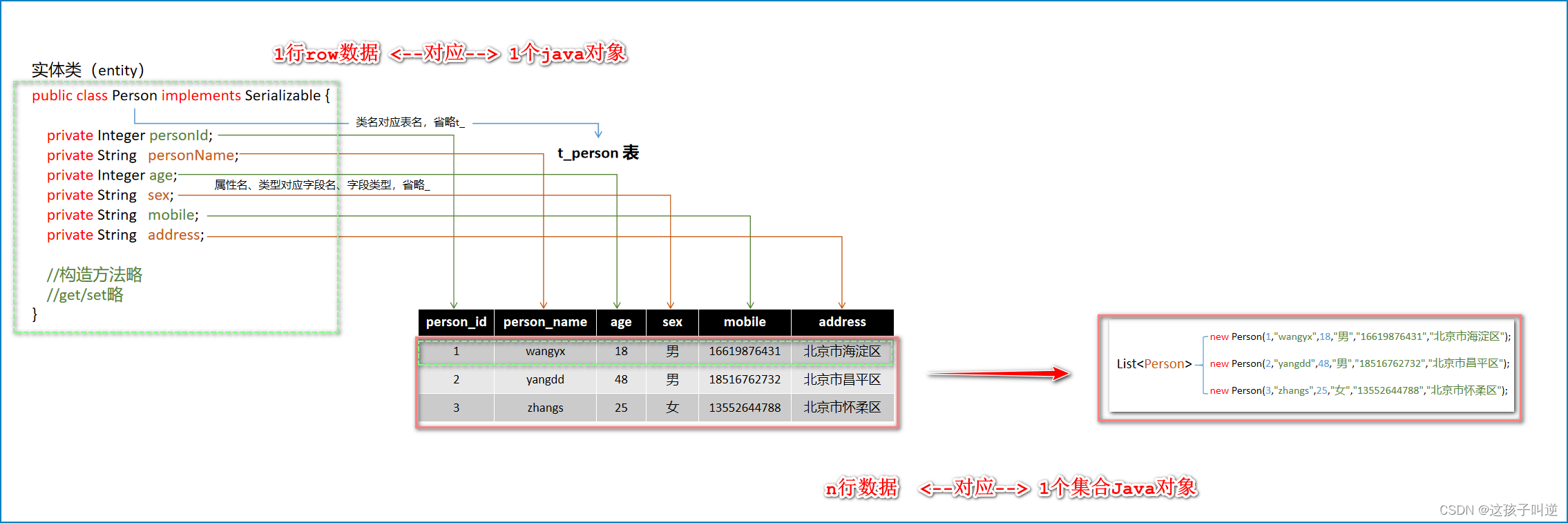
用list存储多项式系数，直接输出list即可。
算法资料：
有限域_百度百科 (baidu.com)
https://baike.baidu.com/item/%E6%9C%89%E9%99%90%E5%9F%9F/4273049?fr=ge_ala可约多项式_百度百科 (baidu.com)https://baike.baidu.com/item/%E5%8F%AF%E7%BA%A6%E5%A4%9A%E9%A1%B9%E5%BC%8F/18881405
有限域GF(2^8)的四则运算及拉格朗日插值-CSDN博客https://blog.csdn.net/luotuo44/article/details/41645597
代码
import copy
class CPolyEle:
iID: int
lData: list = None # 多项式系数。[i]表示i次项系数
oTag = None
class CPolySet:
sType = 'GF'
iPrime = 2
iDeg = 8 # 多项式次数最大值
lAll: list = [] # 所有
lRedu: list = [] # 可约
lIrredu: list = [] # 不可约
def Sort(self) -> int:
iMulMax = self.iPrime ** self.iDeg
iMax = iMulMax * self.iPrime
# 构造lAll#[
for i in range(iMax):
r = self.CreatePoly(i)
self.lAll.append(r)
# ]
# 标记#[
for i in range(2, iMulMax):
for j in range(i, iMulMax):
a: CPolyEle = self.lAll[i]
b: CPolyEle = self.lAll[j]
r = self.Mul(a.lData, b.lData)
if len(r) > self.iDeg + 1:
break
r = self.ListToID(r)
oPoly: CPolyEle = self.lAll[r]
oPoly.oTag = True
# ]
# 保存结果#[
for it in self.lAll:
oPoly: CPolyEle = it
if oPoly.oTag == True:
self.lRedu.append(oPoly.iID)
else:
self.lIrredu.append(oPoly.iID)
# ]
return len(self.lIrredu)
def CreatePoly(self, iID) -> CPolyEle:
ret = CPolyEle()
ret.iID = iID
ret.lData = []
while True:
r = iID % self.iPrime
ret.lData.append(r)
if iID < self.iPrime:
break
iID = iID // self.iPrime
# end while
return ret
def ListToID(self, lPoly: list) -> int:
ret = 0
iMul = 1
for it in lPoly:
ret += it * iMul
iMul *= self.iPrime
return ret
def Add(self, a: list, b: list) -> list:
ret = []
lAdd = a
if (len(a) > len(b)):
ret = copy.deepcopy(a)
lAdd = b
else:
ret = copy.deepcopy(b)
for i in range(len(lAdd)):
ret[i] = (ret[i] + lAdd[i]) % self.iPrime
return ret
def Mul(self, a, b) -> list:
ret: list = [0 for _ in range(len(a))]
if type(b) is int:
for i in range(len(a)):
ret[i] = (a[i] * b) % self.iPrime
elif type(b) is list:
for i in range(len(b)):
lAdd = a
lAdd = self.Mul(lAdd, b[i])
lAdd = self.MulX(lAdd, i)
ret = self.Add(ret, lAdd)
return ret
def MulX(self, a, x) -> list:
lZero = [0 for _ in range(x)]
return lZero + a
def Print(self, iID: int):
print(self.lAll[iID].lData)
def Main():
oTest = CPolySet()
r = oTest.Sort()
print(r)
for it in oTest.lIrredu:
oTest.Print(it)
print('end')
return
if __name__ == '__main__':
Main()
运行结果
73
[0]
[1]
[0, 1]
[1, 1]
[1, 1, 1]
[1, 1, 0, 1]
[1, 0, 1, 1]
[1, 1, 0, 0, 1]
[1, 0, 0, 1, 1]
[1, 1, 1, 1, 1]
[1, 0, 1, 0, 0, 1]
[1, 0, 0, 1, 0, 1]
[1, 1, 1, 1, 0, 1]
[1, 1, 1, 0, 1, 1]
[1, 1, 0, 1, 1, 1]
[1, 0, 1, 1, 1, 1]
[1, 1, 0, 0, 0, 0, 1]
[1, 0, 0, 1, 0, 0, 1]
[1, 1, 1, 0, 1, 0, 1]
[1, 1, 0, 1, 1, 0, 1]
[1, 0, 0, 0, 0, 1, 1]
[1, 1, 1, 0, 0, 1, 1]
[1, 0, 1, 1, 0, 1, 1]
[1, 1, 0, 0, 1, 1, 1]
[1, 0, 1, 0, 1, 1, 1]
[1, 1, 0, 0, 0, 0, 0, 1]
[1, 0, 0, 1, 0, 0, 0, 1]
[1, 1, 1, 1, 0, 0, 0, 1]
[1, 0, 0, 0, 1, 0, 0, 1]
[1, 0, 1, 1, 1, 0, 0, 1]
[1, 1, 1, 0, 0, 1, 0, 1]
[1, 1, 0, 1, 0, 1, 0, 1]
[1, 0, 0, 1, 1, 1, 0, 1]
[1, 1, 1, 1, 1, 1, 0, 1]
[1, 0, 0, 0, 0, 0, 1, 1]
[1, 1, 0, 1, 0, 0, 1, 1]
[1, 1, 0, 0, 1, 0, 1, 1]
[1, 0, 1, 0, 1, 0, 1, 1]
[1, 0, 1, 0, 0, 1, 1, 1]
[1, 1, 1, 1, 0, 1, 1, 1]
[1, 0, 0, 0, 1, 1, 1, 1]
[1, 1, 1, 0, 1, 1, 1, 1]
[1, 0, 1, 1, 1, 1, 1, 1]
[1, 1, 0, 1, 1, 0, 0, 0, 1]
[1, 0, 1, 1, 1, 0, 0, 0, 1]
[1, 1, 0, 1, 0, 1, 0, 0, 1]
[1, 0, 1, 1, 0, 1, 0, 0, 1]
[1, 0, 0, 1, 1, 1, 0, 0, 1]
[1, 1, 1, 1, 1, 1, 0, 0, 1]
[1, 0, 1, 1, 0, 0, 1, 0, 1]
[1, 1, 1, 1, 1, 0, 1, 0, 1]
[1, 1, 0, 0, 0, 1, 1, 0, 1]
[1, 0, 1, 0, 0, 1, 1, 0, 1]
[1, 0, 0, 1, 0, 1, 1, 0, 1]
[1, 0, 0, 0, 1, 1, 1, 0, 1]
[1, 1, 1, 0, 1, 1, 1, 0, 1]
[1, 1, 0, 1, 1, 1, 1, 0, 1]
[1, 1, 1, 0, 0, 0, 0, 1, 1]
[1, 1, 0, 1, 0, 0, 0, 1, 1]
[1, 0, 1, 1, 0, 0, 0, 1, 1]
[1, 1, 1, 1, 1, 0, 0, 1, 1]
[1, 1, 0, 0, 0, 1, 0, 1, 1]
[1, 0, 0, 1, 0, 1, 0, 1, 1]
[1, 0, 0, 0, 1, 1, 0, 1, 1]
[1, 0, 1, 1, 1, 1, 0, 1, 1]
[1, 1, 0, 0, 0, 0, 1, 1, 1]
[1, 1, 1, 1, 0, 0, 1, 1, 1]
[1, 1, 1, 0, 1, 0, 1, 1, 1]
[1, 0, 1, 1, 1, 0, 1, 1, 1]
[1, 1, 1, 0, 0, 1, 1, 1, 1]
[1, 1, 0, 0, 1, 1, 1, 1, 1]
[1, 0, 1, 0, 1, 1, 1, 1, 1]
[1, 0, 0, 1, 1, 1, 1, 1, 1]
end
如果算上0和1，则GF(2)上 次数小于等于8 的 不可约多项式 共有73个
---完---
