目录
1.前缀和
1.一维前缀和
例题:【模板】前缀和
2.二维前缀和
例题:【模板】二维前缀和
2.差分
1.一维差分
1.性质:d[i]的前缀和等于a[i]
2.性质:后缀区间修改
例题:【模板】差分
2.二维差分
例题:【模板】二维差分
例题:鼠鼠我鸭
1.前缀和
1.一维前缀和
前缀我们用prefix来表示
在最开始,我们有一个名为a和一个名为prefix的数组
那么prefix[2]的值就为a[1]+a[2]
prefix[3]的值就为a[1]+a[2]+a[3]
那么如何达成这一目的呢,我们用一下这段代码
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 1; i <= n; i++)
prefix[i] = prefix[i - 1] + a[i];例题:【模板】前缀和

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
ll a[N];
ll prefix[N];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t,n,q;
cin >> t;
while(t--)
{
cin >> n >> q;
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 1; i <= n; i++)
prefix[i] = prefix[i - 1] + a[i];
while(q--)
{
int l,r;
cin >> l >> r;
cout << prefix[r] - prefix[l - 1] << '\n';
}
}
return 0;
}2.二维前缀和
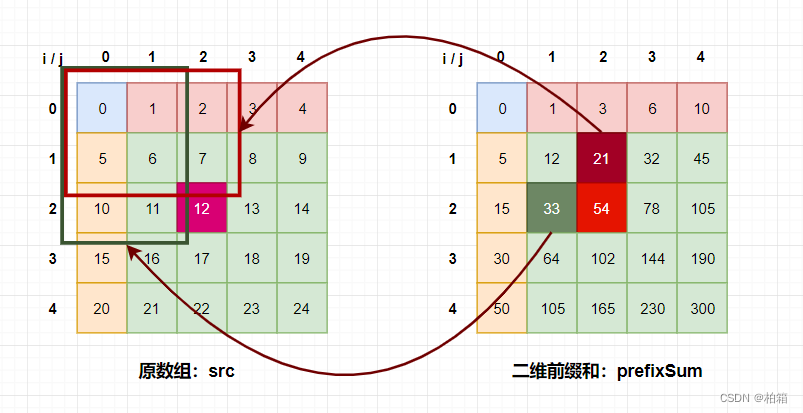
prefix[i][j]表示的是从a[1][1]到a[i][j]之间所有数的和
举例:
| a数组 | 1 | 2 | 3 |
| 1 | |||
| 2 | |||
| 3 |
p3,3 = p2,3 + p3,2 - p2,2 + a3,3
由此可推出
pi,j = pi-1,j + pi,j-1 - pi - 1,j - 1 + ai,j
例题:【模板】二维前缀和

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3 + 10;
ll a[N][N],p[N][N];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,m,q;
cin >> n >> m >> q;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> a[i][j];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
p[i][j] = p[i - 1][j] + p[i][j - 1] - p[i - 1][j - 1] + a[i][j];
while(q--)
{
int x1,y1,x2,y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << p[x2][y2] - p[x1 - 1][y2] - p[x2][y1 - 1] + p[x1 - 1][y1 - 1] << '\n';
}
return 0;
}
2.差分
1.一维差分
差分数组,命名为d
则d[i] = a[i] - a[i-1](i >= 2)
d[1] = a[1]
1.性质:d[i]的前缀和等于a[i]
举例:
a[3] = d[1] + d[2] + d[3]
可以通过前缀还原为a[i]
2.性质:后缀区间修改
由性质1可知,当我们修改一个d的值时,从它下标开始往后的a数组都会相当的改变那么多的值
举例:
我们让d[3]加1,那么a[3],a[4],a[5]......都会加1。
如果我们再让d[6]减1,就可以使得只有a[3]到a[5]加了1这样的操作。
这样的后缀区间修改,是一个静态的,只能先修改再询问。
例题:【模板】差分

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
ll a[N];
ll prefix[N];
ll diff[N];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,p,q;
cin >> n >> p >> q;
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 1; i <= n; i++)
diff[i] = a[i] - a[i - 1];
while(p--)
{
int l,r,x;
cin >> l >> r >> x;
diff[l] += x;
diff[r + 1] -= x;
}
for(int i = 1; i <= n; i++)
a[i] = diff[i] + a[i - 1];
for(int i = 1; i <= n; i++)
prefix[i] = prefix[i - 1] + a[i];
while(q--)
{
int l,r;
cin >> l >> r;
cout << prefix[r] - prefix[l - 1] << '\n';
}
return 0;
}2.二维差分
二维差分的规则为:


性质与一维差分相同
例题:【模板】二维差分
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3 + 10;
ll a[N][N],d[N][N];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,m,q;
cin >> n >> m >> q;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> a[i][j];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
d[i][j] += a[i][j];
d[i+1][j+1] += a[i][j];
d[i+1][j] -= a[i][j];
d[i][j+1] -= a[i][j];
}
while(q--)
{
int x1,y1,x2,y2,c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
d[x1][y1] += c;
d[x2 + 1][y1] -= c;
d[x1][y2+1] -= c;
d[x2+1][y2+1] += c;
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + d[i][j];
cout << a[i][j] << " ";
}
cout << '\n';
}
return 0;
}例题:鼠鼠我鸭
每次释放魔法,会改变最终的结果
假设这个魔法从第一个动物开始使用直到最后一个动物
我们用prefix[i]来表示从第一个动物开始直到第i个动物释放了魔法后算出来的总重量与未释放魔法时的总重量的偏移量
我们找到最小的偏移量的那个坐标和值,并且继续往后移动找到最大的那个偏移量
用最大减去最小,再加上未释放魔法的重量即为答案
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
ll a[N],w[N],prefix[N];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
}
for(int i = 1; i <= n; i++)
{
cin >> w[i];
}
//不释放魔法时的答案
ll ess = 0;
for(int i = 1; i <= n; i++)
{
if(a[i] == 1)
ess += w[i];
}
for(int i = 1; i <= n; i++)
{
prefix[i] = prefix[i - 1] + w[i] * (a[i] == 1 ? -1 : 1);
//释放魔法后原来如果是1,答案会减少
}
ll fix = 0,mi = 0;
for(int i = 1; i <= n; i++)
{
fix = max(fix,prefix[i] - mi);
mi = min(mi,prefix[i]);
}
cout << fix + ess << '\n';
}
return 0;
}







![基于SpringBoot开发的校刊投稿系统[附源码]](https://img-blog.csdnimg.cn/direct/54d86e3a1a29409f80cdad06c0c0bbc4.png)
![[word] word大小写快捷键是什么? #知识分享#学习方法#笔记](https://img-blog.csdnimg.cn/img_convert/aebb5cbcc027319d208baff296fdc85b.jpeg)
