LeetCode_17_中等_电话号码的字母组合

news2024/10/5 18:30:50

文章目录

1. 题目
2. 思路及代码实现（Python）
- 2.1 回溯

1. 题目

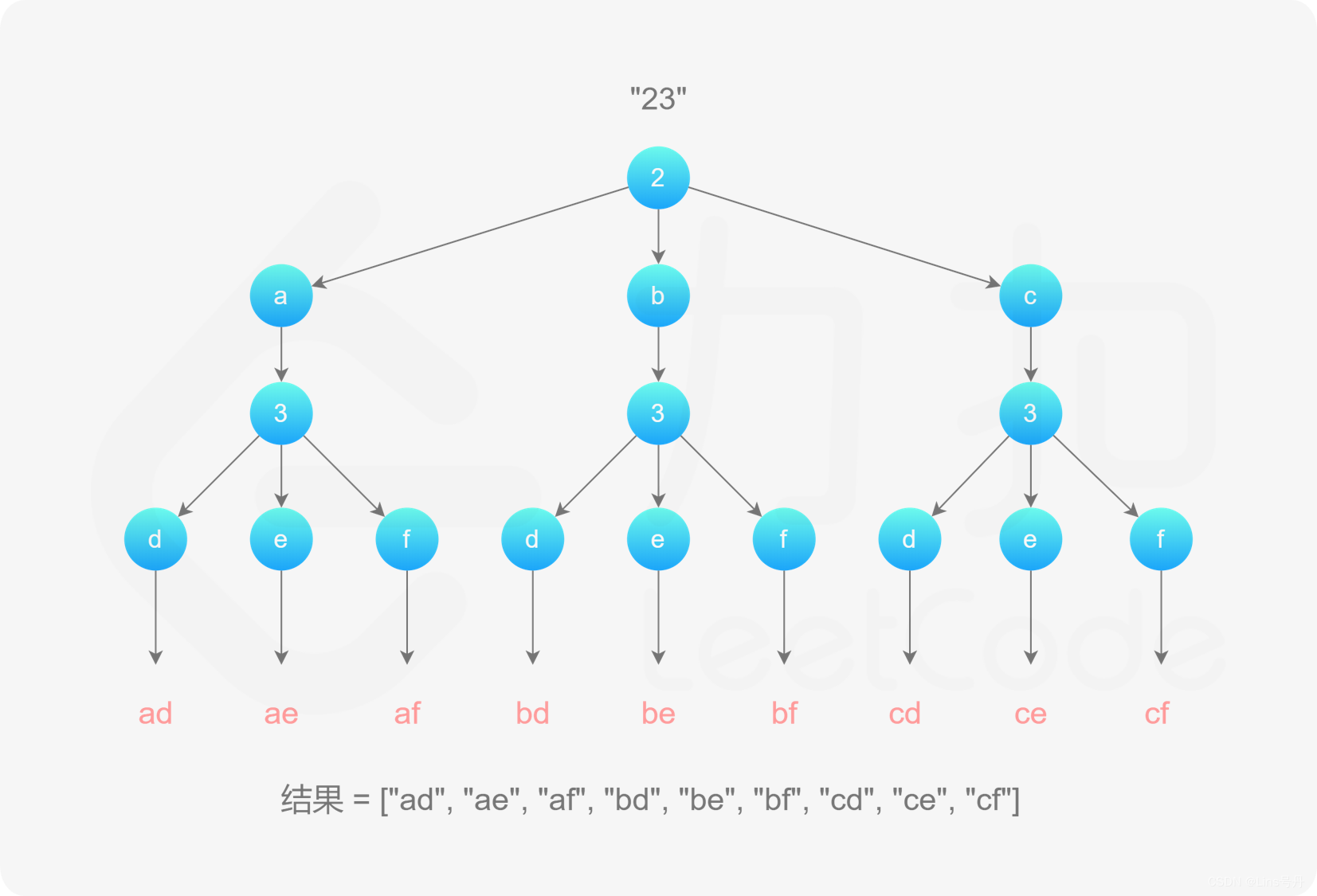
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
在这里插入图片描述
示例 1：

输入： $d i g i t s = "23"$
输出： $[" a d ", " a e ", " a f ", " b d ", " b e ", " b f ", " c d ", " ce ", " c f "]$

示例 2：

输入： $d i g i t s = ""$
输出： $[]$

示例 3：

输入： $d i g i t s = "2"$
输出： $[" a ", " b ", " c "]$

提示：

$0 <= d i g i t s . l e n g t h <= 4$
$d i g i t s [i]$ 是范围 $[^{'} 2^{'},^{'} 9^{'}]$ 的一个数字。

2. 思路及代码实现（Python）

2.1 回溯

首先使用哈希表存储每个数字对应的所有可能的字母，然后进行回溯操作。回溯过程中维护一个字符串，表示已有的字母排列（如果未遍历完电话号码的所有数字，则已有的字母排列是不完整的）。该字符串初始为空。每次取电话号码的一位数字，从哈希表中获得该数字对应的所有可能的字母，并将其中的一个字母插入到已有的字母排列后面，然后继续处理电话号码的后一位数字，直到处理完电话号码中的所有数字，即得到一个完整的字母排列。然后进行回退操作，遍历其余的字母排列。

回溯算法用于寻找所有的可行解，如果发现一个解不可行，则会舍弃不可行的解。在这道题中，由于每个数字对应的每个字母都可能进入字母组合，因此不存在不可行的解，直接穷举所有的解即可。

在这里插入图片描述

时间复杂度： $O(3^m \times 4^n)$ )，其中 $m$ 是输入中对应 $3$ 个字母的数字个数（包括数字 $2$ 、 $3 、 4 、 5 、 6 、 8$ ）， $n$ 是输入中对应 $4$ 个字母的数字个数（包括数字 $7 、 9$ ， $m + n$ 是输入数字的总个数。当输入包含 $m$ 个对应 $3$ 个字母的数字和 $n$ 个对应 $4$ 个字母的数字时，不同的字母组合一共有 $3^m \times 4^n$ 种，需要遍历每一种字母组合。空间复杂度主要是递归调用的占用： $O (m + n)$ 。

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return list()
        
        phoneMap = {
            "2": "abc",
            "3": "def",
            "4": "ghi",
            "5": "jkl",
            "6": "mno",
            "7": "pqrs",
            "8": "tuv",
            "9": "wxyz",
        }

        def backtrack(index: int):
            if index == len(digits):
                combinations.append("".join(combination))
            else:
                digit = digits[index]
                for letter in phoneMap[digit]:
                    combination.append(letter)
                    backtrack(index + 1)
                    combination.pop()

        combination = list()
        combinations = list()
        backtrack(0)
        return combinations