一、网络延迟时间
力扣第743题

本题采用最短路径的思想进行求解
1.1 具体思路
(1)使用邻接表表示有向图:首先,我们可以使用邻接表来表示有向图。邻接表是一种数据结构,用于表示图中顶点的相邻关系。在这个问题中,我们可以使用字典(Python 中的 defaultdict)来实现邻接表,其中键是源节点,值是一个列表,包含了从该源节点出发的边以及对应的传递时间。
(2)使用最短路径算法计算从节点 K 到其他节点的最短路径:我们可以使用 Dijkstra 算法或者 Bellman-Ford 算法来计算从节点 K 到其他所有节点的最短路径。这些算法可以帮助我们找到从节点 K 出发,到达其他节点的最短路径长度。在这个问题中,我们可以使用 Dijkstra 算法,它能够高效地处理正权重边的最短路径问题。
(3)找出最长的最短路径:最后,我们找出所有最短路径中的最大值,即找到信号传递到所有节点所需的时间。这是因为信号需要经过最长的最短路径才能传递到所有节点。如果有节点无法收到信号,我们将返回-1。
1.2 思路展示
假设我们有以下有向图和起始节点 K:
图示例:

起始节点 K = 2
对应的邻接表为:
{
2: [(1, 2), (3, 1)],
3: [(4, 1)],
1: [(3, 1), (4, 2)]
}
然后使用 Dijkstra 算法来计算从节点 2 出发到其他节点的最短路径。过程如下:
从节点 2 出发,到达节点 1 的距离为 2,到达节点 3 的距离为 1。
选择距离最短的节点 3,然后更新节点 3 相邻节点的距离:到达节点 4 的距离为 2。
最终得到的最短路径为:从节点 2 出发到节点 1 的最短路径长度为 2,到节点 3 的最短路径长度为 1,到节点 4 的最短路径长度为 2。
最长的最短路径为 2,即信号传递到所有节点所需的时间为 2。
1.3 代码实现
-
import collections import heapq def networkDelayTime(times, n, k): # 构建邻接表表示的有向图 graph = collections.defaultdict(list) for u, v, w in times: graph[u].append((v, w)) # 使用 Dijkstra 算法计算最短路径 pq = [(0, k)] # 优先队列,存储节点及当前距离 dist = {} # 存储从节点 K 到各节点的最短路径长度 while pq: d, node = heapq.heappop(pq) if node in dist: continue dist[node] = d for nei, d2 in graph[node]: if nei not in dist: heapq.heappush(pq, (d + d2, nei)) # 找出最长的最短路径,即找到信号传递到所有节点所需的时间 if len(dist) == n: return max(dist.values()) else: return -1 # 示例输入 times = [[2, 1, 1], [2, 3, 1], [3, 4, 1]] n = 4 k = 2 # 输出结果 print(networkDelayTime(times, n, k))1.4 复杂度分析
这段代码使用了Dijkstra算法来计算最短路径,下面是对其时间复杂度的分析:
构建邻接表表示的有向图:遍历times列表中的每个元素,时间复杂度为O(E),其中E为times的长度。
使用Dijkstra算法计算最短路径:最坏情况下,需要遍历所有的节点和边。每次从优先队列中弹出距离最小的节点,时间复杂度为O(logN),其中N为节点的总数。在每个节点上,需要遍历其邻居节点,时间复杂度为O(K),其中K为节点的平均邻居节点数。因此,总的时间复杂度为O((N+K)logN)。
找出最长的最短路径:遍历dist字典中的所有值,时间复杂度为O(N)。
综上所述,整体的时间复杂度为O(E + (N+K)logN + N)。空间复杂度为O(N+E),其中N为节点的总数,E为边的总数。
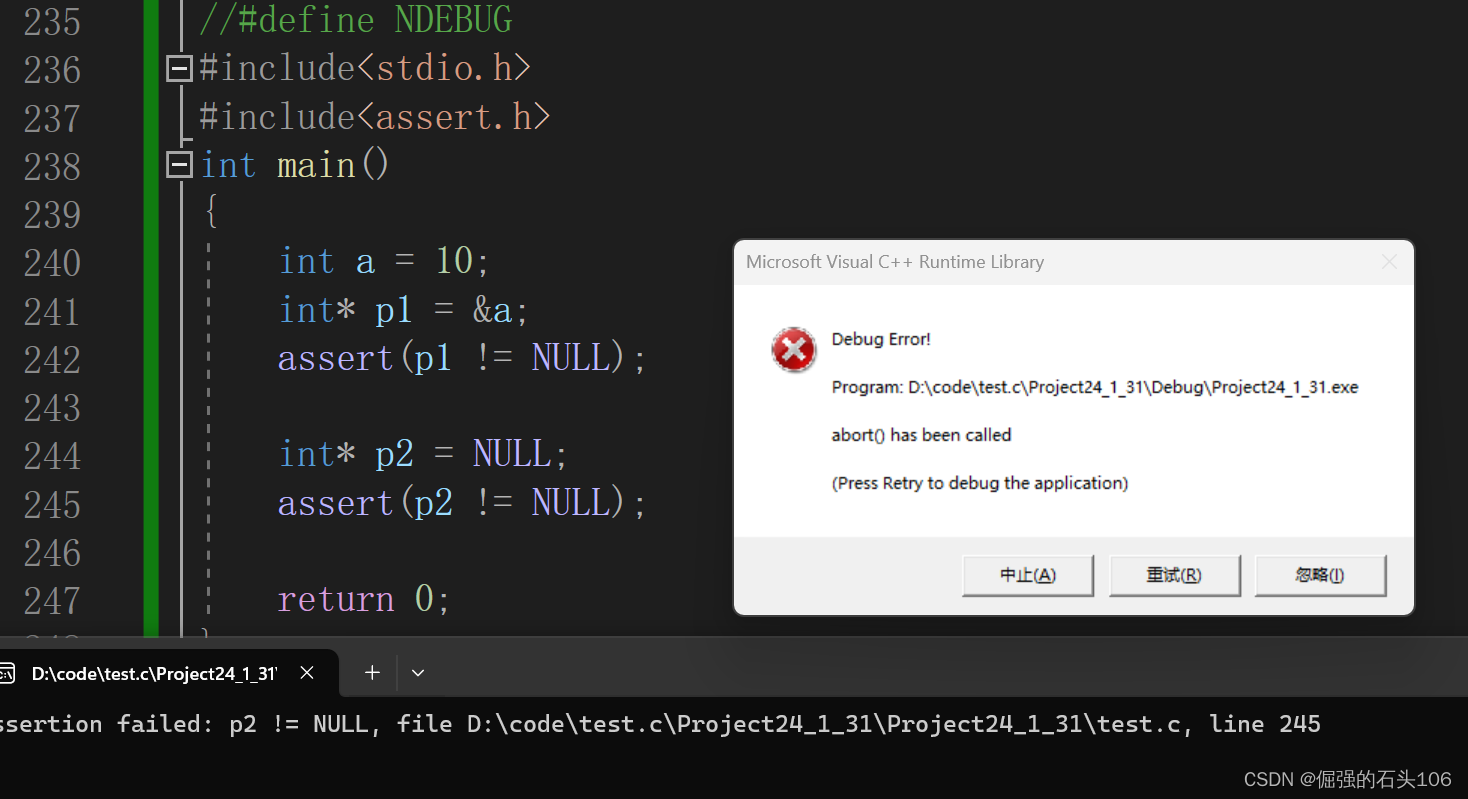
1.5 运行结果
# 示例输入
times = [[2, 1, 1], [2, 3, 1], [3, 4, 1]]
n = 4
k = 2
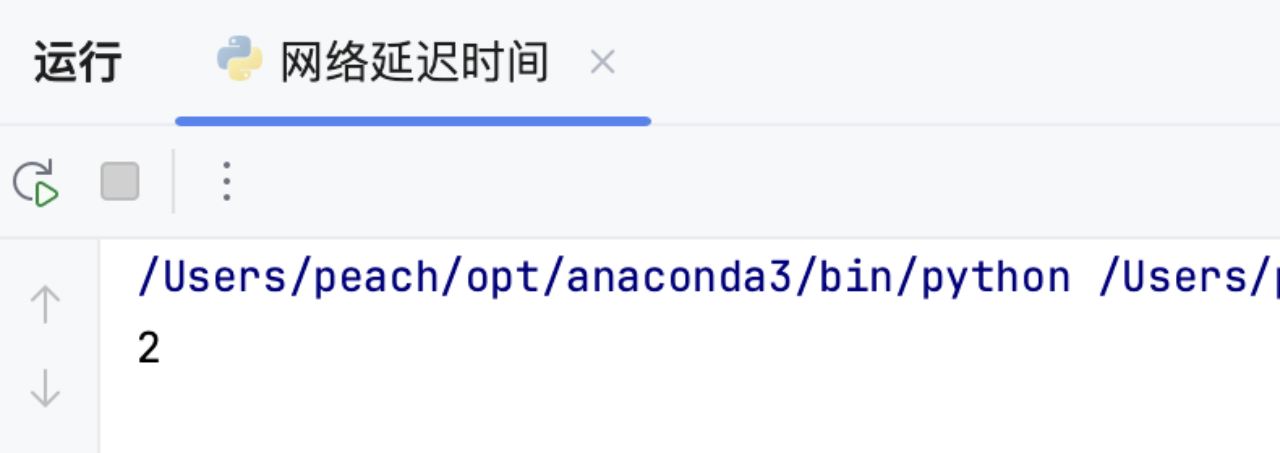
运行结果与预期一致
二、概率最大的路径
力扣第1514题

本题依旧采用最短路径的思想解决
2.1 具体思路
可以使用Dijkstra算法来解决。
首先构建无向加权图:使用字典graph来表示图,键为节点编号,值为一个列表,表示与该节点相邻的节点及对应的边权重。遍历edges和succProb两个列表,将节点和对应的边权重添加到graph中。
初始化距离列表和概率列表:使用列表dist和probs来分别存储从起点到每个节点的最短距离和成功概率。将起点的最短距离设置为1,其余节点的最短距离设置为0,起点的成功概率设置为1,其余节点的成功概率设置为0。
使用Dijkstra算法计算最短路径:使用堆优化的Dijkstra算法来计算从起点到每个节点的最短距离和成功概率。首先将起点加入优先队列pq。在每次循环中,从优先队列中弹出距离最小的节点node,遍历与该节点相邻的节点nei。如果从起点到nei的路径的成功概率乘以nei到node的边权重大于从起点到node的最短距离,并且这个概率乘以边权重大于nei节点当前的成功概率,则更新nei节点的最短距离和成功概率,并将(nei, -距离)添加到优先队列中。
返回终点的成功概率:如果终点的成功概率大于0,则返回终点的成功概率,否则返回0。
2.2 思路展示
假设给定无向加权图,其中节点0到节点3的成功概率最大。
首先,我们将这个图构建成一个字典graph,如下所示:
graph = {
0: [(1, -math.log(0.5)), (2, -math.log(0.2))],
1: [(0, -math.log(0.5)), (2, -math.log(0.5))],
2: [(0, -math.log(0.2)), (1, -math.log(0.5)), (3, -math.log(0.3))],
3: [(2, -math.log(0.3))]
}
接下来,我们初始化距离和概率列表,如下所示:
dist = [0, 0, 0, 0]
probs = [0, 0, 0, 0]
dist[0] = 1
probs[0] = 1
然后,我们使用Dijkstra算法计算最短路径。首先将起点0加入优先队列pq。在第一次循环中,从优先队列中弹出距离最小的节点0,遍历与该节点相邻的节点1和2。由于从起点到节点1的路径的成功概率乘以1到0的边权重(即-log(0.5))等于0.5,大于从起点到节点0的最短距离1,并且这个概率乘以边权重大于节点1当前的成功概率0,则更新节点1的最短距离和成功概率,并将(1, -距离)添加到优先队列中。同样的,我们也会更新节点2的最短距离和成功概率。
在第二次循环中,从优先队列中弹出距离最小的节点1,遍历与该节点相邻的节点0和2。由于从起点到节点0的路径的成功概率乘以1到0的边权重等于0.5,大于从起点到节点1的最短距离并且这个概率乘以边权重大于节点0当前的成功概率0,则更新节点0的最短距离和成功概率,并将(0, -距离)添加到优先队列中。同时,我们也会更新节点2的最短距离和成功概率。
在第三次循环中,从优先队列中弹出距离最小的节点2,遍历与该节点相邻的节点0、1和3。由于从起点到节点3的路径的成功概率乘以2到3的边权重(即-log(0.3))等于0.8,大于从起点到节点2的最短距离并且这个概率乘以边权重大于节点3当前的成功概率0,则更新节点3的最短距离和成功概率,并将(3, -距离)添加到优先队列中。我们也会更新节点0和1的最短距离和成功概率。
在最后一次循环中,从优先队列中弹出距离最小的节点3,发现它没有相邻的节点,结束Dijkstra算法的计算过程。
最后,我们返回终点3的成功概率0.25。
2.3 代码实现
import heapq
import math
from collections import defaultdict
def maxProbability(n, edges, succProb, start, end):
# 构建无向带权图
graph = defaultdict(list)
for i in range(len(edges)):
u, v = edges[i]
p = succProb[i]
graph[u].append((v, -math.log(p)))
graph[v].append((u, -math.log(p)))
# 初始化概率列表
probs = [0] * n
probs[start] = 1
# 使用Dijkstra算法计算最大成功概率路径
pq = [(-1, start)]
while pq:
prob, node = heapq.heappop(pq)
prob = -prob # 取相反数以便按概率从大到小排序
if node == end:
return prob
for nei, edge_prob in graph[node]:
new_prob = prob * math.exp(edge_prob)
if new_prob > probs[nei]:
probs[nei] = new_prob
heapq.heappush(pq, (-new_prob, nei))
# 如果没有从起点到终点的路径,则返回0
return 0
# 示例测试
n = 3
edges = [[0,1],[1,2],[0,2]]
succProb = [0.5,0.5,0.2]
start = 0
end = 2
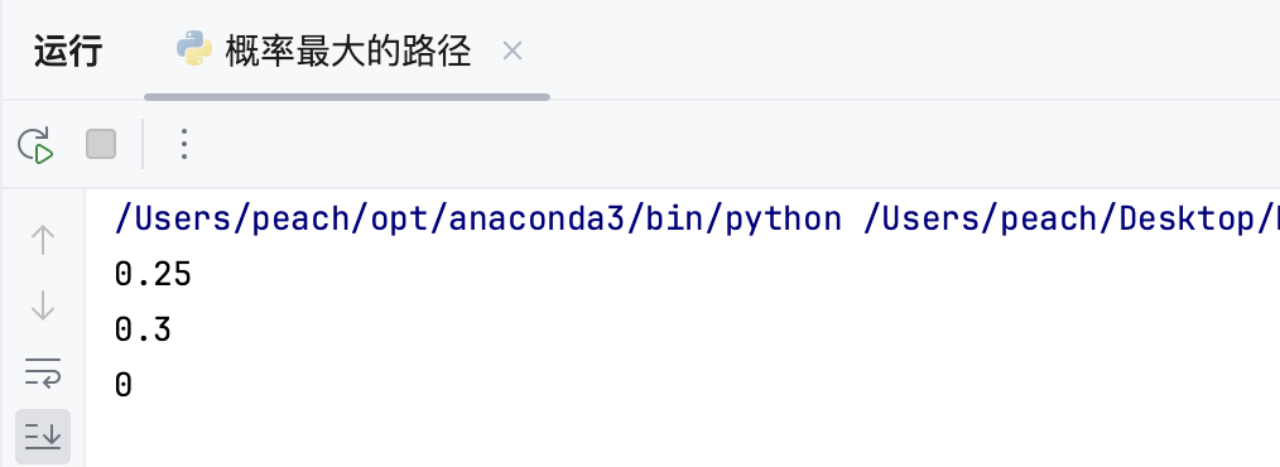
print(maxProbability(n, edges, succProb, start, end)) # 输出: 0.25
succProb = [0.5,0.5,0.3]
print(maxProbability(n, edges, succProb, start, end)) # 输出: 0.3
edges = [[0,1]]
succProb = [0.5]
print(maxProbability(n, edges, succProb, start, end)) # 输出: 02.4 复杂度分析
这段代码的时间复杂度为 O(ElogV),其中 E 是边数,V 是节点数。这是因为在 Dijkstra 算法中,每条边最多会被遍历一次,而堆的插入和弹出操作的时间复杂度为 O(logV),因此总时间复杂度为 O(ElogV)。
空间复杂度为 O(V),主要是用来存储概率列表和堆。
2.5 运行结果
与预期结果均保持一致
三、最小路径和
力扣第64题

本题采用动态规划的思想解决
3.1 具体思路
定义一个二维数组 dp,其大小为 m x n。其中 dp[i][j] 表示从左上角到达网格位置 (i, j) 的最小路径和。
初始化第一行和第一列的路径和,因为只能向右或向下移动,所以第一行的路径和为前一个位置的路径和加上当前位置的值,第一列的路径和同理。
对于其他位置 (i, j),可以从上方或左方移动过来,选择路径和较小的那个路径,并加上当前位置的值。
遍历整个网格,更新 dp 数组中的路径和,直到达到右下角位置 (m-1, n-1)。
返回 dp[m-1][n-1],即右下角位置的最小路径和。
3.2 思路展示
假设输入的网格为:
1 3 1
1 5 1
4 2 1
首先定义一个二维数组 dp,其大小为 m x n。其中 dp[i][j] 表示从左上角到达网格位置 (i, j) 的最小路径和。
0 0 0
0 0 0
0 0 0
然后初始化第一行和第一列的路径和,因为只能向右或向下移动,所以第一行的路径和为前一个位置的路径和加上当前位置的值,第一列的路径和同理。
1 4 5
2 0 0
6 0 0
对于其他位置 (i, j),可以从上方或左方移动过来,选择路径和较小的那个路径,并加上当前位置的值。
1 4 5
2 7 6
6 8 7
遍历整个网格,更新 dp 数组中的路径和,直到达到右下角位置 (m-1, n-1)。
最后返回 dp[m-1][n-1],即右下角位置的最小路径和。
3.3 代码实现
def minPathSum(grid):
m, n = len(grid), len(grid[0])
dp = [[0] * n for _ in range(m)]
# 初始化第一行和第一列的路径和
dp[0][0] = grid[0][0]
for i in range(1, m):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, n):
dp[0][j] = dp[0][j-1] + grid[0][j]
# 动态规划更新路径和
for i in range(1, m):
for j in range(1, n):
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
return dp[m-1][n-1]
# 示例测试
grid = [[1,3,1],[1,5,1],[4,2,1]]
print(minPathSum(grid)) # 输出: 7
grid = [[1,2,3],[4,5,6]]
print(minPathSum(grid)) # 输出: 123.4 复杂度分析
这段代码的时间复杂度为 O(m*n),其中 m 和 n 分别是网格的行数和列数。这是因为代码中使用了两层嵌套的循环来遍历整个网格,并更新 dp 数组中的路径和。
空间复杂度为 O(m*n),因为创建了一个与网格大小相同的二维数组 dp,用于存储路径和。
总结起来,这段代码通过动态规划的思想,利用一个二维数组记录从左上角到达每个位置的最小路径和,最后返回右下角位置的路径和。时间和空间复杂度都是网格的大小,因此在实践中,如果网格较大,可能需要考虑优化算法或使用其他方法来减少时间和空间开销。
3.5 运行结果
# 示例测试
grid = [[1,3,1],[1,5,1],[4,2,1]]
print(minPathSum(grid)) # 输出: 7
grid = [[1,2,3],[4,5,6]]
print(minPathSum(grid)) # 输出: 12
运行结果均与预期一致
结尾语
选择大于努力!

2025-2-2