目录
1 基础知识
1.1 空指针
1.2 结构体
1.3 指针访问
1.4 三目运算符
2 160. 相交链表
3 206. 反转链表
4 234. 回文链表
菜鸟做题第三周,语言是 C++
1 基础知识
1.1 空指针
使用 nullptr 来判断是否为空指针:
if (headA == nullptr)“NULL 在 C++ 中就是 0,这是因为在 C++ 中 void* 类型是不允许隐式转换成其他类型的,所以之前 C++ 中用 0 来代表空指针,但是在重载整型的情况下,会出现上述的问题。所以,C++11 加入了 nullptr,可以保证在任何情况下都代表空指针,而不会出现上述的情况,因此,建议以后还是都用 nullptr 替代 NULL 吧,而 NULL 就当做 0 使用。”
摘自博客:C++ 中 NULL 和 nullptr 的区别
1.2 结构体
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};- val 和 next 都是结构体 ListNode 中的元素
- val 表示当前链表节点的值
- next 表示指向下一个链表节点的指针
- ListNode(int x) : val(x), next(NULL) {} 是初始化方法
1.3 指针访问
ListNode * p;
p->val; // 访问值
p->next; // 访问下一节点指针1.4 三目运算符
pA = pA == nullptr ? headB : pA->next;其中,“?” 前的是判断条件,“?” 后的是两个选项,“:” 前的是条件成立时选择的选项,“:” 后的是条件不成立时选择的选项。这里的 “pA == nullptr” 是判断条件,“headB” 是 “pA == nullptr” 成立时 “pA” 等于的值,“pA->next” 是 “pA == nullptr” 不成立时 “pA” 等于的值。
三目运算符不是为了装逼用的,真的可以在很多情况下简化判断结构。
2 160. 相交链表
妈呀,这是我大一下程算课期末的真题
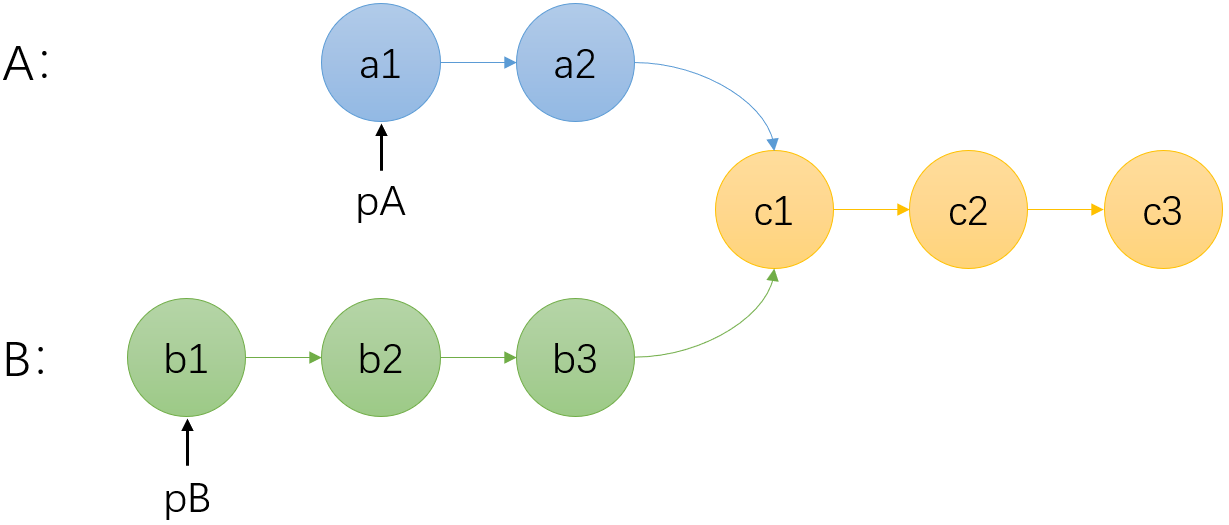
解题思路:
假设蓝色段的长度为 a,绿色段的长度为 b,黄色段的长度为 c 。定义 pA 和 pB 两个指针,pA 遍历完 a + c 后遍历 b,pB 遍历完 b + c 后遍历 a,判断:
- 若 pA 和 pB 相遇且节点不为空,则表明两条链表相交
- 若 pA 和 pB 未相遇或节点为空,则表明两条链表不相交
这种解法用到了一点数学思想:
即 pA 和 pB 最终都会到达同一位置,它们在该位置指向的节点是否一致决定了链表是否相交。
如有疑问请参考官方题解,它的分情况讨论更加详细。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (headA == nullptr || headB == nullptr) {
return nullptr;
}
ListNode * pA = headA, * pB = headB;
while (pA != pB) {
pA = pA == nullptr ? headB : pA->next;
pB = pB == nullptr ? headA : pB->next;
}
return pA;
}
};3 206. 反转链表
解题思路:把所有节点的 next 指针全部反向即可。
思路说明图:
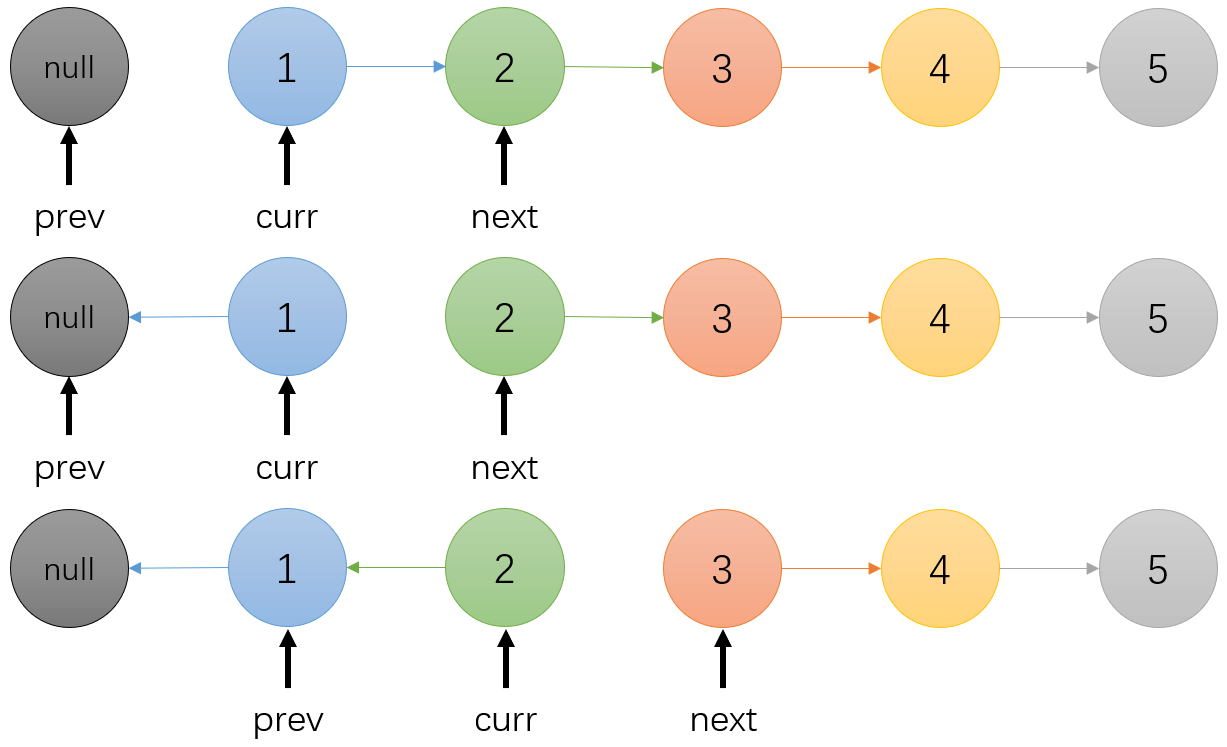
对于这种反转问题,核心思想就是把已经遍历过的、但还需要用到的位置保存下来。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode * prev = nullptr;
ListNode * curr = head;
while (curr) {
ListNode * next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
};4 234. 回文链表
解题思路:
- 遍历链表,把所有 val 存入一个数组中
- 遍历数组的前半段,判断里面的 val 是否和后半段的 val 对称
class Solution {
public:
bool isPalindrome(ListNode* head) {
ListNode * p = head;
vector<int> vals;
while (p) {
vals.push_back(p->val);
p = p->next;
}
for (int i = 0; i < vals.size() / 2 + 1; ++i) {
if (vals[i] != vals[vals.size() - i - 1]) return false;
}
return true;
}
};