更多精彩内容尽在数字孪生平台。
简要
我们首先想象一个场景,根据用户位置找出给定半径内有哪些咖啡店。最直接的做法是检查数据集中所有咖啡店的纬度/经度位置是否落在给定半径内。虽然我们可以轻松地做到这一点,但在 n 个位置的数组中,我们必须访问 n-1 个位置,这基本上会花费 O(n) 时间。
空间数据库(例如 Postgis)使用更有效的方法进行空间查询,其中一种便是四叉树算法。与许多算法一样,四叉树还可用于地理空间以外的应用,例如游戏中的碰撞检测、图像处理或数据可视化。四叉树也是 Geohashes 的概念基础,这是一种常见的公共域地理编码系统,可将地理位置编码为短的字母和数字字符串。
算法实现
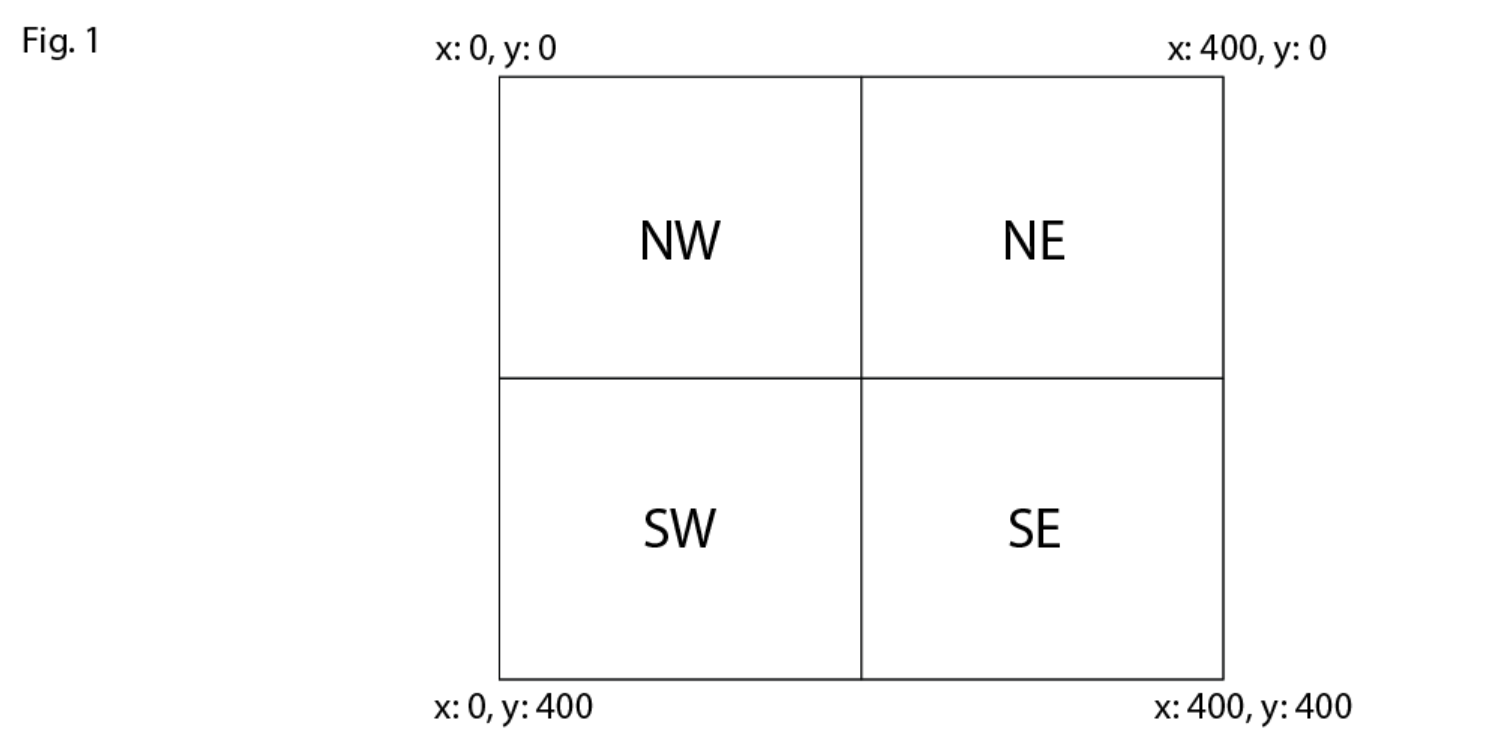
顾名思义,该算法适用于四棵(“四边形quad”)树。我们不是像上面的例子那样查看每个点,而是递归地扫描四个quad以检查它们中的任何一个是否与我们的搜索范围重叠。在这里,我们做个约定,为每个象限选择的命名是 NW、NE、SW、SE。该算法是针对 2d 平面实现的,其中 x:0 和 y:0 位于左上角(见图 1)。
Step1
首先我们必须将给定的点数组(如咖啡店位置)插入到四叉树中:
- 定义最大容量
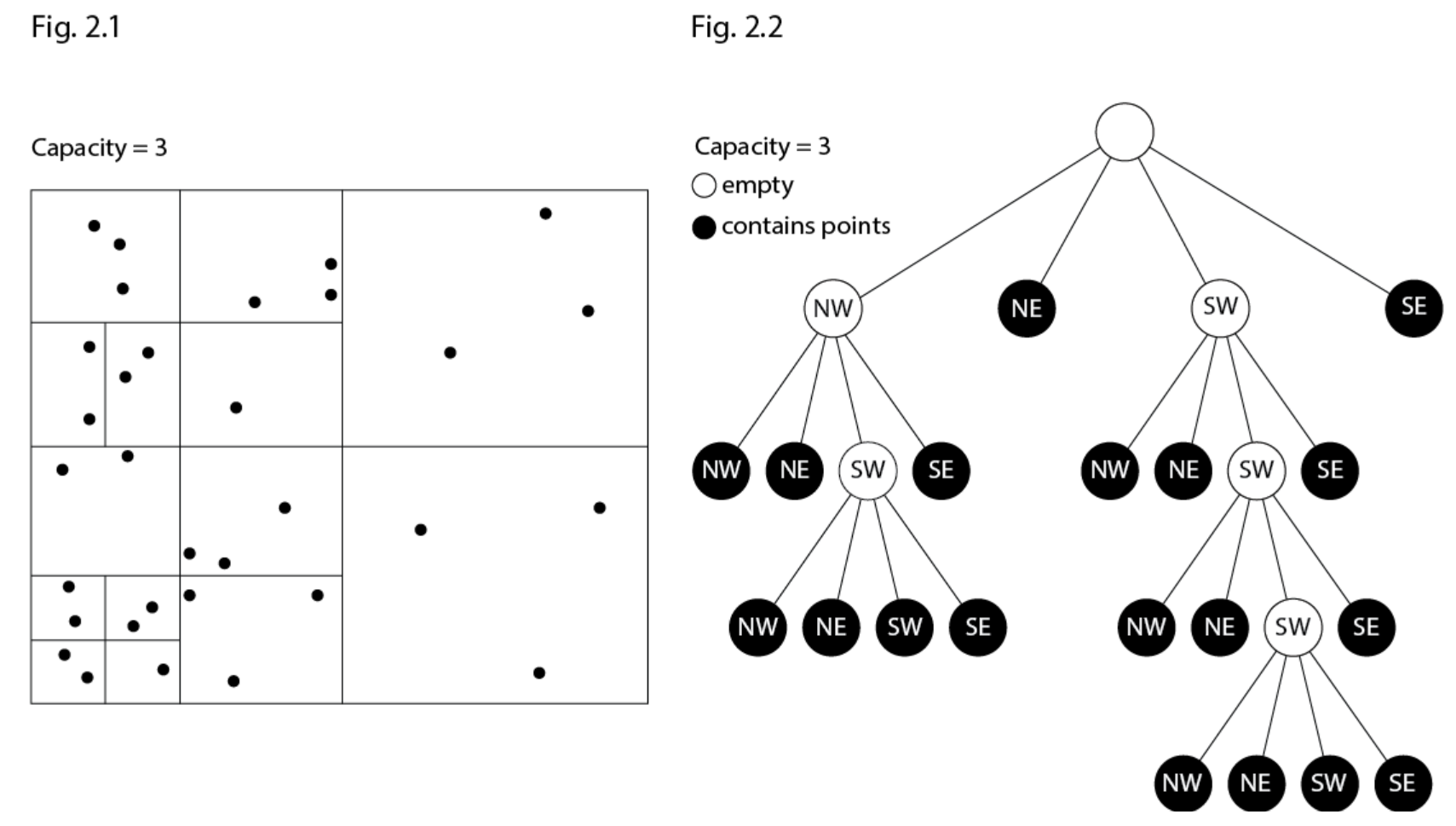
self.capacity。该算法将递归地将点添加到包含该点和最大值的quad中。容量将告诉我们一个quad可以容纳多少个点。 - 下面是将一个点插入到四叉树类中的函数(有关如何构建该类的更多详细信息,请查看源代码)。仅当该点包含在
self.bound中时才会执行,self.bound定义了我们的quad边界。如果该点包含在self.bound中,我们有两个选择: ①如果尚未达到容量且没有细分,我们将其附加到当前quad;②如果达到容量并且quad尚未细分,我们将当前quad细分为四个新的子quad。在这里,我们还必须将主quad的点重新分配给子项并“清理”主quad。然后,我们将该点插入到正确的子quad中。 - 对数组中的每个点重复上述过程。图 2.1 和 2.2 显示了可视化 32 个点和容量 3 的整个插入过程的两种不同方式。
def insert(self, point):
if self.bound.contains(point):
if len(self.points) <= self.capacity and self.isDivided == False:
self.points.append(point)
else: #capacity is reached
if not self.isDivided:
self.subdivide()
for p in self.points:
self.nw.insert(p)
self.ne.insert(p)
self.sw.insert(p)
self.se.insert(p)
self.points = [] #clean main
self.nw.insert(point)
self.ne.insert(point)
self.sw.insert(point)
self.se.insert(point)
Step2
然后我们实现一个查询函数来查找搜索范围内的点。
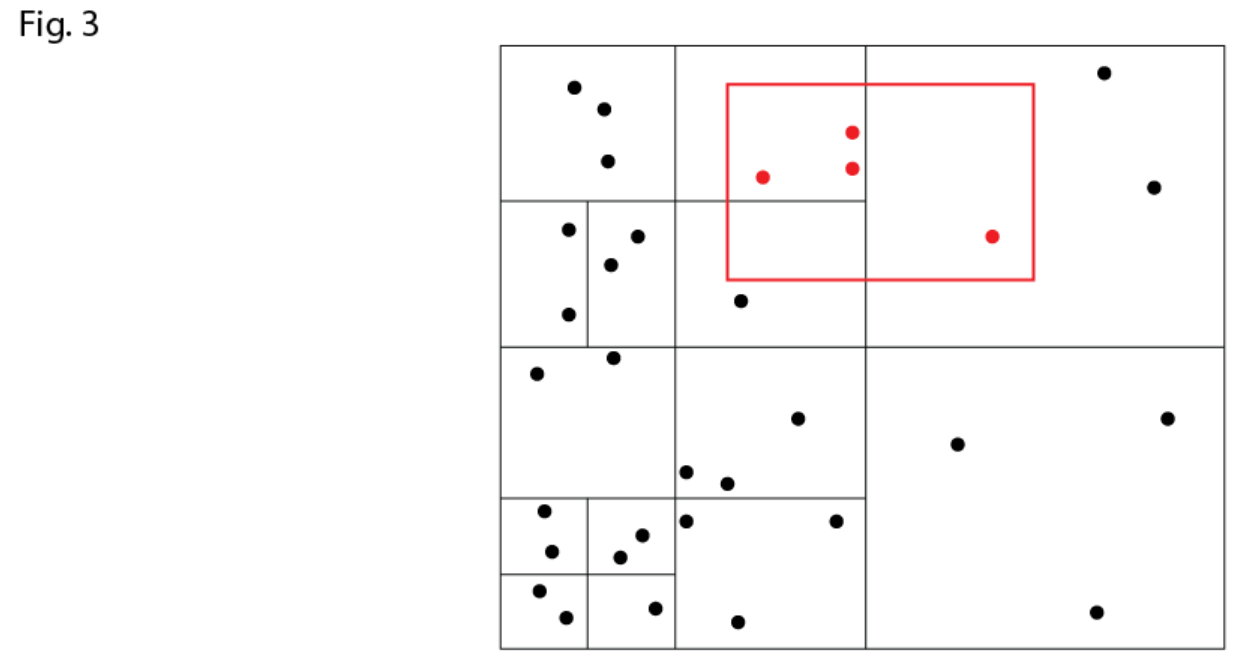
图3展现了红色矩形搜索区域的示例。如图所示,搜索区域内的点可以位于不同的quad上,这意味着我们必须从不同的quad中检索点。
我们定义矩形搜索区域对象为 myrange , 输入到查询函数中。为了找到这个点,我们检查搜索范围是否与我们正在查看的quad相交。如果没有,返回一个空的找到的数组;如果是,我们将在found数组中收集点。为此,我们首先检查quad是否有子对象。如果是,我们将继续寻找子节点;如果没有,我们将添加当前quad中的点。
请注意,有两种方法可以在当前quad中附加点: 如果 myrange 包含整个quad区域,则我们附加所有点;否则,我们必须检查quad上的每个点,看看它是否与 myrange 重叠。
def query(self, myrange):
found = []
if not self.bound.intersects(myrange): #no intersection between bounding box and quad
return found
else:
if self.isDivided:
found.append(self.nw.query(myrange))
found.append(self.ne.query(myrange))
found.append(self.sw.query(myrange))
found.append(self.se.query(myrange))
else:
if myrange.contains(self.bound):
found.append(self.points)
else:
for p in self.points:
if myrange.contains(p):
found.append(p)
return found
时间复杂度
与二分搜索算法类似,该算法允许我们将搜索时间缩短至 O(log(n))。