关于小麦麦穗或者是麦粒相关的开发实践不多,但前文也有所涉及,感兴趣的话可以自行移步阅读即可:
《基于轻量级yolov5n+CBAM开发构建全球小麦麦穗智能检测计数系统》
《基于YOLOv5[n/s/m/l/x]全系列参数模型开发构建小麦麦穗颗粒智能化精准检测识别计数系统》
这里我们的想法是基于Transformer预测头对YOLOv5进行改进优化,进而开发构建用于小麦麦穗检测计数的模型,首先看下实例效果:

接下来简单看下数据集:


实例数据标注实例如下:
0 0.600781 0.94375 0.042188 0.04375
0 0.433594 0.676562 0.101562 0.05625
0 0.802344 0.428125 0.042188 0.0625
0 0.135156 0.915625 0.067187 0.071875
0 0.141406 0.549219 0.079687 0.057813
0 0.175781 0.973437 0.070312 0.053125
0 0.078125 0.019531 0.09375 0.039062
0 0.33125 0.251563 0.059375 0.05625
0 0.25625 0.710156 0.075 0.073438
0 0.449219 0.792969 0.092188 0.079687
0 0.457031 0.34375 0.070312 0.078125
0 0.028125 0.520312 0.05625 0.0625
0 0.214844 0.525781 0.117188 0.064062
0 0.691406 0.210938 0.073438 0.0875
0 0.569531 0.798438 0.082812 0.115625
0 0.935937 0.303906 0.065625 0.073438
0 0.459375 0.411719 0.103125 0.060937
0 0.782031 0.346875 0.054688 0.059375
0 0.95 0.175781 0.078125 0.070312
0 0.08125 0.235937 0.084375 0.078125
0 0.696094 0.352344 0.079687 0.089063
0 0.207813 0.916406 0.084375 0.067187
0 0.357031 0.732812 0.070312 0.053125
0 0.763281 0.821875 0.117188 0.08125
0 0.666406 0.629687 0.092188 0.0625
0 0.445312 0.469531 0.09375 0.079687
0 0.023438 0.146875 0.046875 0.059375
0 0.679688 0.126562 0.059375 0.071875
0 0.850781 0.980469 0.073438 0.039062
0 0.169531 0.739062 0.117188 0.065625
0 0.189062 0.599219 0.06875 0.070312
0 0.621875 0.283594 0.09375 0.073438
0 0.849219 0.867969 0.057813 0.057813
0 0.696875 0.723437 0.05625 0.05625
0 0.099219 0.34375 0.098437 0.06875
0 0.336719 0.892969 0.070312 0.089063
0 0.714844 0.46875 0.092188 0.06875
0 0.971094 0.296094 0.057813 0.051562
0 0.044531 0.935156 0.082812 0.082812
0 0.492969 0.028125 0.070312 0.05625
0 0.9625 0.830469 0.071875 0.089063
0 0.297656 0.889062 0.073438 0.071875
0 0.914844 0.561719 0.092188 0.082812
0 0.057031 0.43125 0.076563 0.06875
0 0.628125 0.557813 0.096875 0.05625
0 0.092188 0.65625 0.10625 0.0875
作者原论文如下:
《TPH-YOLOv5: Improved YOLOv5 Based on Transformer Prediction Head for Object Detection on Drone-captured Scenarios》



详情可以自行阅读原论文即可。
训练数据配置文件如下:
# Dataset
path: ./dataset
train:
- images/train
val:
- images/test
test:
- images/test
nc: 1 # number of classes
# Classes
names:
0: wheat这里给出模型文件,如下所示:
# YOLOv5 🚀 by Ultralytics, GPL-3.0 license
# Parameters
nc: 1 # number of classes
depth_multiple: 0.33 # model depth multiple
width_multiple: 0.50 # layer channel multiple
anchors: 4
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
# YOLOv5 v6.0 head
head:
[[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[ -1, 1, Conv, [ 128, 1, 1 ] ],
[ -1, 1, nn.Upsample, [ None, 2, 'nearest' ] ],
[ [ -1, 2 ], 1, Concat, [ 1 ] ], # cat backbone P2
[ -1, 2, C3STR, [ 128, False ] ], # 21 (P2/4-xsmall)
[ -1, 1, Conv, [ 128, 3, 2 ] ],
[ [ -1, 18, 4], 1, Concat, [ 1 ] ], # cat head P3
[ -1, 2, C3STR, [ 256, False ] ], # 24 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14, 6], 1, Concat, [1]], # cat head P4
[-1, 2, C3STR, [512, False]], # 27 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 2, C3STR, [1024, False]], # 30 (P5/32-large)
[[21, 24, 27, 30], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
与原始基准模型保持相同的实验参数设置,进行模型的训练,等待开发训练完成,我们来整体对其进行对比分析。
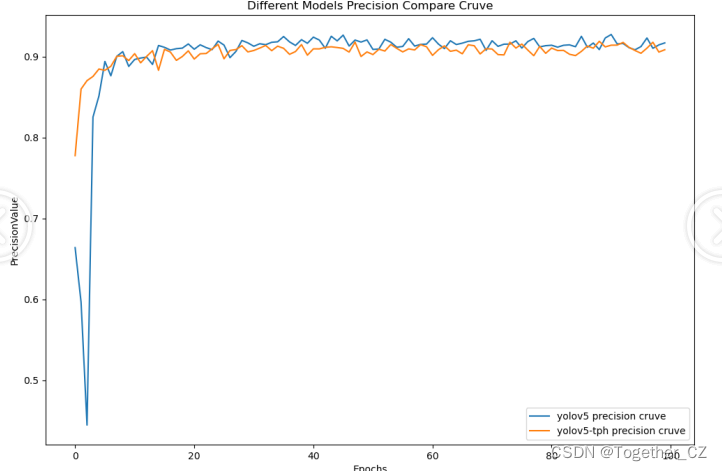
【Precision曲线】
精确率曲线(Precision-Recall Curve)是一种用于评估二分类模型在不同阈值下的精确率性能的可视化工具。它通过绘制不同阈值下的精确率和召回率之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率(Precision)是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率曲线。
根据精确率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察精确率曲线,我们可以根据需求确定最佳的阈值,以平衡精确率和召回率。较高的精确率意味着较少的误报,而较高的召回率则表示较少的漏报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
精确率曲线通常与召回率曲线(Recall Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
【Recall曲线】
召回率曲线(Recall Curve)是一种用于评估二分类模型在不同阈值下的召回率性能的可视化工具。它通过绘制不同阈值下的召回率和对应的精确率之间的关系图来帮助我们了解模型在不同阈值下的表现。
召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。召回率也被称为灵敏度(Sensitivity)或真正例率(True Positive Rate)。
绘制召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的召回率和对应的精确率。
将每个阈值下的召回率和精确率绘制在同一个图表上,形成召回率曲线。
根据召回率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察召回率曲线,我们可以根据需求确定最佳的阈值,以平衡召回率和精确率。较高的召回率表示较少的漏报,而较高的精确率意味着较少的误报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
召回率曲线通常与精确率曲线(Precision Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。

【F1值曲线】
F1值曲线是一种用于评估二分类模型在不同阈值下的性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)、召回率(Recall)和F1分数的关系图来帮助我们理解模型的整体性能。
F1分数是精确率和召回率的调和平均值,它综合考虑了两者的性能指标。F1值曲线可以帮助我们确定在不同精确率和召回率之间找到一个平衡点,以选择最佳的阈值。
绘制F1值曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率、召回率和F1分数。
将每个阈值下的精确率、召回率和F1分数绘制在同一个图表上,形成F1值曲线。
根据F1值曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
F1值曲线通常与接收者操作特征曲线(ROC曲线)一起使用,以帮助评估和比较不同模型的性能。它们提供了更全面的分类器性能分析,可以根据具体应用场景来选择合适的模型和阈值设置。

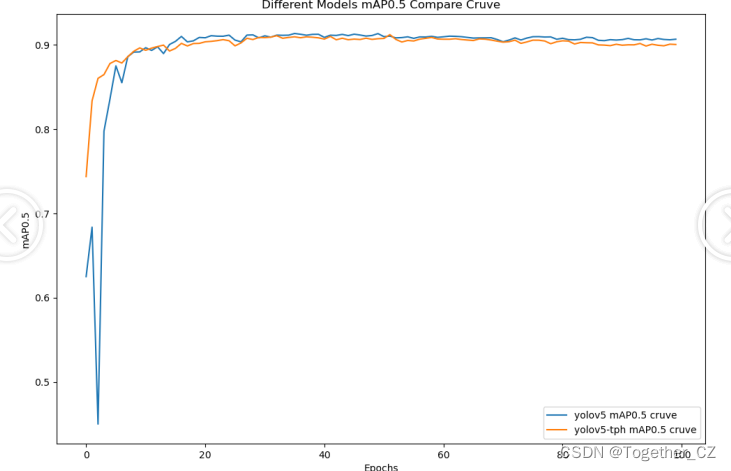
【mAP0.5】
mAP0.5(mean Average Precision at 0.5 IoU)
mAP0.5表示在IoU(交并比)阈值为0.5的情况下计算的平均精度(Average Precision,AP)。
IoU阈值决定了何时认为检测框与真实框匹配。较高的IoU阈值意味着更严格的匹配标准。
mAP0.5主要关注低阈值下的性能,即当IoU接近0.5时,模型在识别重叠框时的准确性。
【mAP0.5:0.95】
mAP0.5:0.95(mean Average Precision over IoU thresholds from 0.5 to 0.95):
mAP0.5:0.95表示在多个IoU阈值(从0.5到0.95)下计算的平均精度。
它涵盖了从低到高的IoU阈值,更全面地评估了模型在不同IoU阈值下的性能。
mAP0.5:0.95可以帮助我们了解模型在不同重叠程度下的检测能力。

从上面指标对比情况来看,tph改进的模型与原模型交叉领先没有明显的差距,接下来我们详细看戏tph模型结果
【PR曲线】
精确率-召回率曲线(Precision-Recall Curve)是一种用于评估二分类模型性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)和召回率(Recall)之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率-召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率-召回率曲线。
根据曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
精确率-召回率曲线提供了更全面的模型性能分析,特别适用于处理不平衡数据集和关注正例预测的场景。曲线下面积(Area Under the Curve, AUC)可以作为评估模型性能的指标,AUC值越高表示模型的性能越好。

【训练可视化】

【Batch实例】

最后,我们对其各个指标进行统计直方图对比可视化如下所示:
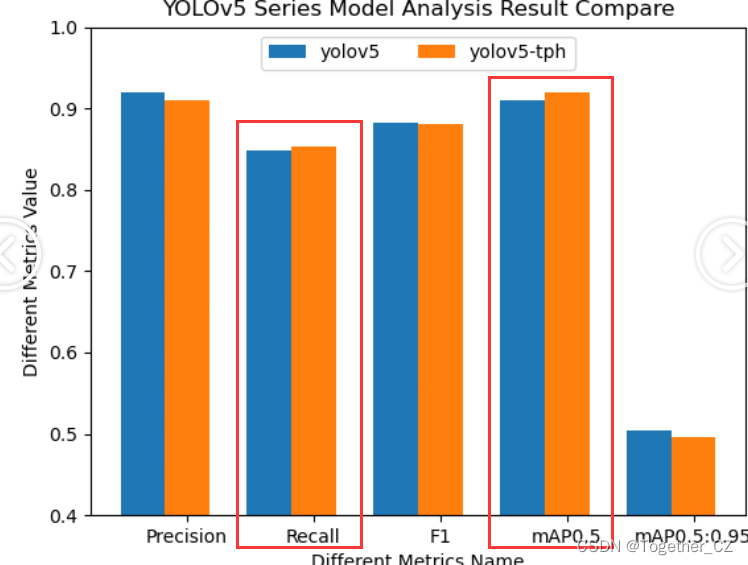
可以看到:改进的TPH-YOLOv5模型在召回率和mAP0.5上略优于原生模型,在其他几个指标上则略逊于原生模型,可见模型的改进本身并不一定能提升模型的效果,打破原生固有的生态平衡可能适得其反。
感兴趣的话也可以基于自己的数据场景开发对比实验尝试下,可能会得到不一样的结果。