以贝尔数为基础,参考杨辉三角形,也可以生成贝尔三角形(Bell triangle),也称为艾特肯阵列(Aitken's Array),皮埃斯三角形(Peirce Triangle)。
贝尔三角形的构造方法:
(1)第一行第一个元素是1,即a[1][1] = 1
(2)对于n>1,第n行第一项等于第n-1行最后一项,即a[n][1] = a[n-1][n-1];
(3)对于m,n>1,第n行第m项等于它左边和左上方的两个数之和,即a[n][m] = a[n][m-1] + a[n-1][m-1];
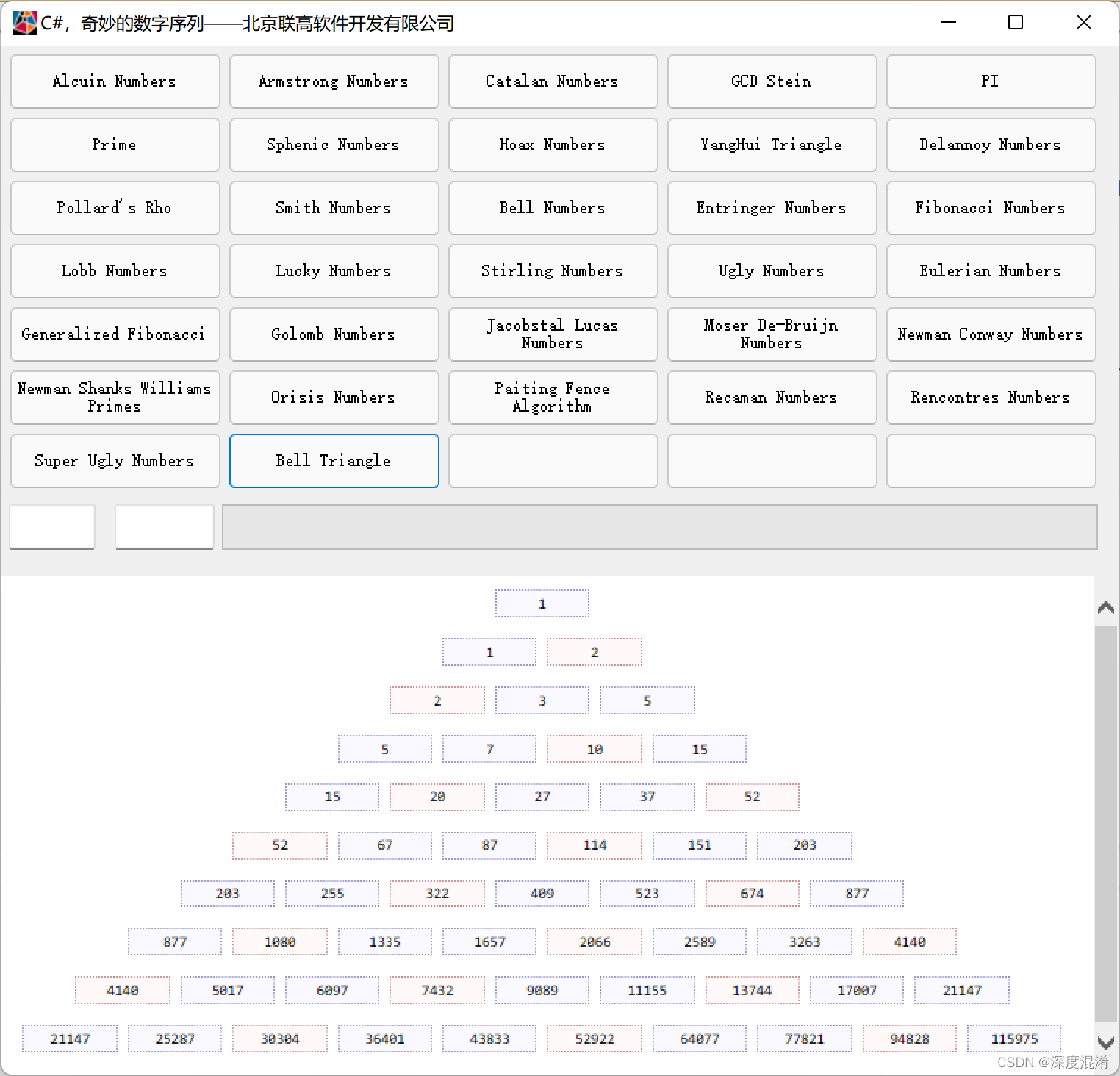
1 文本格式
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
/// <summary>
/// 贝尔三角形(Bell triangle)
/// 艾特肯阵列(Aitken's Array)
/// 皮埃斯三角形(Peirce Triangle)
/// </summary>
/// <param name="n"></param>
/// <returns></returns>
public static string Bell_Triangle(int n)
{
StringBuilder sb = new StringBuilder();
sb.AppendLine("<style>");
sb.AppendLine(".n0 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #993333;background-color:#FFF9F9;margin-right:10px;margin-bottom:10px; } ");
sb.AppendLine(".n1 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #333399;background-color:#F9F9FF;margin-right:10px;margin-bottom:10px; } ");
sb.AppendLine("</style>");
sb.AppendLine("<center>");
long[] last = new long[n + 1];
long[] array = new long[n + 1];
last[0] = 1;
for (int i = 1; i <= n; i++)
{
sb.AppendLine("<table><tr><td>");
array[0] = (i > 1) ? last[i - 2] : last[i - 1];
sb.AppendLine("<div class='n" + (array[0] % 2) + "'>" + array[0] + "</div>");
for (int j = 1; j < i; j++)
{
array[j] = array[j - 1] + last[j - 1];
sb.AppendLine("<div class='n" + (array[j] % 2) + "'>" + array[j] + "</div>");
}
for (int j = 0; j < i; j++)
{
last[j] = array[j];
}
sb.AppendLine("</td></tr></table>");
}
return sb.ToString();
}
}
}
——————————————————————
POWER BY TRUFFER.CN
2 代码格式
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
/// <summary>
/// 贝尔三角形(Bell triangle)
/// 艾特肯阵列(Aitken's Array)
/// 皮埃斯三角形(Peirce Triangle)
/// </summary>
/// <param name="n"></param>
/// <returns></returns>
public static string Bell_Triangle(int n)
{
StringBuilder sb = new StringBuilder();
sb.AppendLine("<style>");
sb.AppendLine(".n0 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #993333;background-color:#FFF9F9;margin-right:10px;margin-bottom:10px; } ");
sb.AppendLine(".n1 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #333399;background-color:#F9F9FF;margin-right:10px;margin-bottom:10px; } ");
sb.AppendLine("</style>");
sb.AppendLine("<center>");
long[] last = new long[n + 1];
long[] array = new long[n + 1];
last[0] = 1;
for (int i = 1; i <= n; i++)
{
sb.AppendLine("<table><tr><td>");
array[0] = (i > 1) ? last[i - 2] : last[i - 1];
sb.AppendLine("<div class='n" + (array[0] % 2) + "'>" + array[0] + "</div>");
for (int j = 1; j < i; j++)
{
array[j] = array[j - 1] + last[j - 1];
sb.AppendLine("<div class='n" + (array[j] % 2) + "'>" + array[j] + "</div>");
}
for (int j = 0; j < i; j++)
{
last[j] = array[j];
}
sb.AppendLine("</td></tr></table>");
}
return sb.ToString();
}
}
}