目录
1.蓝桥小课堂-平方和
2.房顶漏水啦
3.质数王国
4.取余
5.数学尖子生
6.魔术师
比赛链接
1.蓝桥小课堂-平方和
简单签到直接按照题目处理即可注意开long long
void solve(){
LL x; cin>>x;
LL ans= x*(x+1)*(2*x+1)/6;
cout<<ans<<endl;
}2.房顶漏水啦
覆盖正方形的操作我们需要看的是最远的两端即可,所以只需要看长度和宽度的最大值来覆盖即可
void solve(){
cin>>n>>m;
LL mix=1e18,miy=1e18,Max=-1e18,May=-1e18;
while(m--){
LL x,y; cin>>x>>y;
mix=min(x,mix);
Max=max(Max,x);
miy=min(miy,y);
May=max(May,y);
}
LL ans = max((Max-mix+1),(May-miy+1));
cout<<ans<<endl;
}3.质数王国
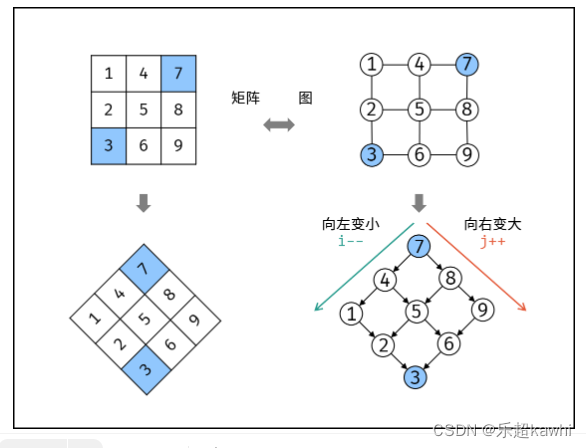
我们可以先使用线性筛处理出所有的质数,接着对两个质数的中间的数进行左右变化处理最小值即可预处理o(n),然后直接求解即可
int cnt;
int primes[N];
void solve(){
cin>>n;
auto get = [&](){
bitset<N> st;
for(int i=2;i<N;i++){
if(!st[i]) primes[cnt++]=i;
for(int j=0;primes[j]<=N/i;j++){
st[i*primes[j]]=true;
if(i%primes[j]==0) break;
}
}
};
get();
vector<int> dp(N);
dp[0]=2,dp[1]=1;
for(int i=1;i<cnt;i++){
for(int x=primes[i-1]+1;x<primes[i];x++){
dp[x]=min(x-primes[i-1],primes[i]-x);
}
}
LL ans=0;
while(n--){
int x; cin>>x;
ans+=dp[x];
}
cout<<ans<<endl;
}4.取余
依照数据范围我们应该是要在o(n)的处理下得到答案,也就是要用到数学知识,我们可以从最开始的 S<=mod<=T这个区间去+b(1-B)这样范围的数,但是时间过高不可取,所以我们考虑使用区间的特性,我们可以转化为(<=T)-(<=S-1)就可以得到在中间这个区间的方案数量.
我们接着枚举b的大小
1.b<=u+1则无论a取多少都可以(a%b<=u)
2.b>u+1则A/i*(u+1)+min(A%i,u); 对于倍数的累加然后加上剩余的即可
void solve(){
LL A,B,S,T; cin>>A>>B>>S>>T;
auto get = [&](LL u){
LL res=0;
if(u<0) return res;
for(int i=1;i<=B;i++){
if(i<=u+1) res+=A;
else res+=A/i*(u+1)+min(A%i,u);
}
return res;
};
cout<<get(T)-get(S-1)<<endl;
}5.数学尖子生
依照题目意思如果我们要找到f(a)=b那么a一定是的倍数,基于这个点我们来处理问题,同时他不是
的倍数的话,我们可以想到那就是做差就是剩下的满足要求的,也就是容斥原理
同时需要注意的是考虑数据范围很可能超过,对于超过的话就是0我们再进行特殊处理即可
LL lcm(LL a,LL b){
return a/__gcd(a,b)*b;
}
void solve(){
vector<LL> lc(N);
auto get = [&](){
lc[0]=1;
for(int i=1;i<N;i++){
lc[i]=lcm(i,lc[i-1]);
if(lc[i]>1e16){
lc[i]=0; break;
}
}
};
get();
cin>>t;
while(t--){
LL n,m;
cin>>n>>m;
if(n==1||lc[n-1]==0){
cout<<0<<endl;
continue;
}
LL ans=m/lc[n-1]-(lc[n] ? m/lc[n] : 0);
cout<<ans<<endl;
}
}6.魔术师
我们可以发现他具有鲜明的区间修改和变化的操作但是他和我们平常的线段树不同他具有几个物品之间的切换之类的操作,对于这些变化,我们线段树变化的核心在于lazy如何修改我们可以在线段树中用懒标记来维护他们之间的关系,如果是翻倍的话也就是自己和自己的关系,关系如何传递,所以我们用二维数组来充当懒标记来处理,然后再用数组进行pushdown的操作来维护
int t,n,m;
int op,ql,qr,A,B;
int add[N*4][3][3],a[N*4][3],now[3][3];
void pushup(int u){
for(int i=0;i<3;i++) a[u][i]=(a[u<<1][i]+a[u<<1|1][i])%mod;
}
void lazy(int a[3][3],int b[3][3]){
int c[3][3];
for(int i=0;i<3;i++)
for(int j=0;j<3;j++){
c[i][j]=0;
for(int k=0;k<3;k++){
c[i][j]=(c[i][j]+(LL)a[i][k]*b[k][j]%mod)%mod;
}
}
// 记录下来关系的传递
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
a[i][j]=c[i][j];
}
void down(int a[3],int b[3][3]){
// 这个区间直接修改
int c[3];
for(int j=0;j<3;j++){
c[j]=0;
for(int k=0;k<3;k++){
c[j]=(c[j]+(LL)a[k]*b[k][j]%mod)%mod;
}
}
for(int i=0;i<3;i++) a[i]=c[i];
}
void build(int u,int l,int r){
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
add[u][i][j]=(i==j);// 表示lazy
if(l==r){
int x; cin>>x;
x--;
a[u][x]=1;
return ;
}
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
void modify(int u,int l,int r){
if(ql<=l && r<=qr){// 找到需要修改的区间
lazy(add[u],now);// 然后加入懒标记
down(a[u],now);
return ;
}
lazy(add[u<<1],add[u]);
lazy(add[u<<1|1],add[u]);
down(a[u<<1],add[u]);
down(a[u<<1|1],add[u]);
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
add[u][i][j]=(i==j);// 表示这个区间的lazy用完了恢复
int mid=l+r>>1;
if(ql<=mid) modify(u<<1,l,mid);
if(qr>mid) modify(u<<1|1,mid+1,r);
pushup(u);
}
void solve(){
cin>>n>>m;
build(1,1,n);
while(m--){
cin>>ql>>qr>>op>>A; A--;
memset(now,0,sizeof now);// 表示传递的性质 1->1 自己到自己等于没有标记
// 表示是否具有标记的传递
for(int i=0;i<3;i++) now[i][i]=1;
if(op==3){
now[A][A]=2;// 自己到自己乘以2
}
else{
cin>>B; B--;
if(op==1) now[A][A]=now[B][B]=0,now[A][B]=now[B][A]=1;
else now[A][A]=0,now[A][B]=1;
}
modify(1,1,n);
for(int i=0;i<3;i++) cout<<a[1][i]<<' ';
cout<<endl;
}
return ;
}