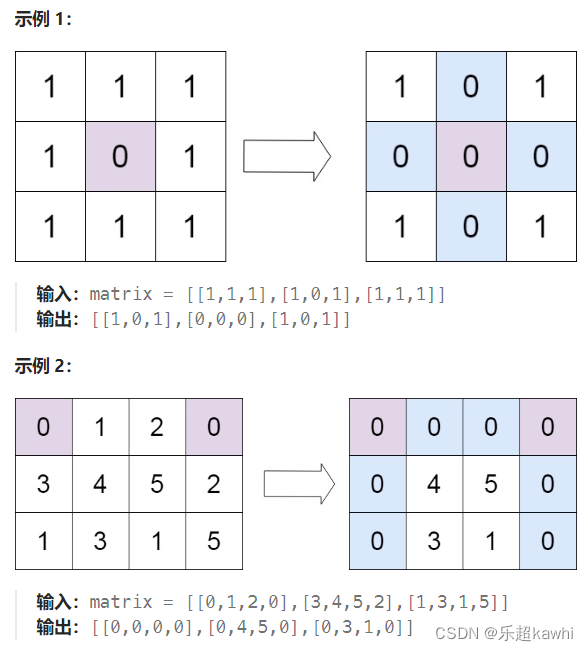
1.73. 矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-2^31 <= matrix[i][j] <= 2^31 - 1
思路:
1)先遍历以便用集合来存0元素的行号与列号,再遍历对出现其中的元素进行清零。
2)关键思想: 用matrix第一行和第一列记录该行该列是否有0,作为标志位。但是对于第一行,和第一列要设置一个标志位,为了防止自己这一行(一列)也有0的情况.注释写在代码里,直接看代码很好理解!
代码:
第一个思路:
class Solution(object):
def setZeroes(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: None Do not return anything, modify matrix in-place instead.
"""
hanghao=set()
liehao=set()
lieshu=len(matrix[0])
for i in range(len(matrix)):
for j in range(lieshu):
if matrix[i][j]==0:
hanghao.add(i)
liehao.add(j)
for i in range(len(matrix)):
for j in range(lieshu):
if i in hanghao or j in liehao:
matrix[i][j]=0
第二个思路:
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
row = len(matrix)
col = len(matrix[0])
row0_flag = False
col0_flag = False
# 找第一行是否有0
for j in range(col):
if matrix[0][j] == 0:
row0_flag = True
break
# 第一列是否有0
for i in range(row):
if matrix[i][0] == 0:
col0_flag = True
break
# 把第一行或者第一列作为 标志位
for i in range(1, row):
for j in range(1, col):
if matrix[i][j] == 0:
matrix[i][0] = matrix[0][j] = 0
#print(matrix)
# 置0
for i in range(1, row):
for j in range(1, col):
if matrix[i][0] == 0 or matrix[0][j] == 0:
matrix[i][j] = 0
if row0_flag:
for j in range(col):
matrix[0][j] = 0
if col0_flag:
for i in range(row):
matrix[i][0] = 0
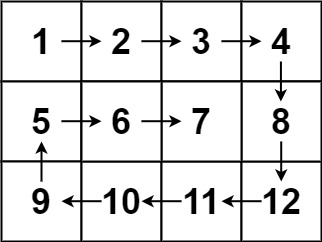
2.54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
思路:
主要就是模拟,关键在于设定上下左右边界。
- 取左边界到右边界,以upper为行,i为列从left到right 将上边界下移++upper
- 取上边界到下边界,以right为列,i为行从upper到down 将右边界左移--right
- 取右边界到左边界,以down为行,i为列从right到left 将下边界上移--down
- 取下边界到上边界,以left为列,i为行从down到upper 将左边界右移++left
代码:
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
int m=matrix.length , n=matrix[0].length;
List<Integer> res=new ArrayList<>();
int upper=0 , down=m-1 , left=0 , right=n-1;
while(true){
for(int i=left;i<=right;i++)res.add(matrix[upper][i]);
if(++upper>down)break;
for(int i=upper;i<=down;i++)res.add(matrix[i][right]);
if(--right<left)break;
for(int i=right;i>=left;i--)res.add(matrix[down][i]);
if(--down<upper)break;
for(int i = down;i>=upper;i--)res.add(matrix[i][left]);
if(++left>right)break;
}
return res;
}
}3.48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
思路:
1)先沿对角线互换,然后逐行对调
2)辅助矩阵
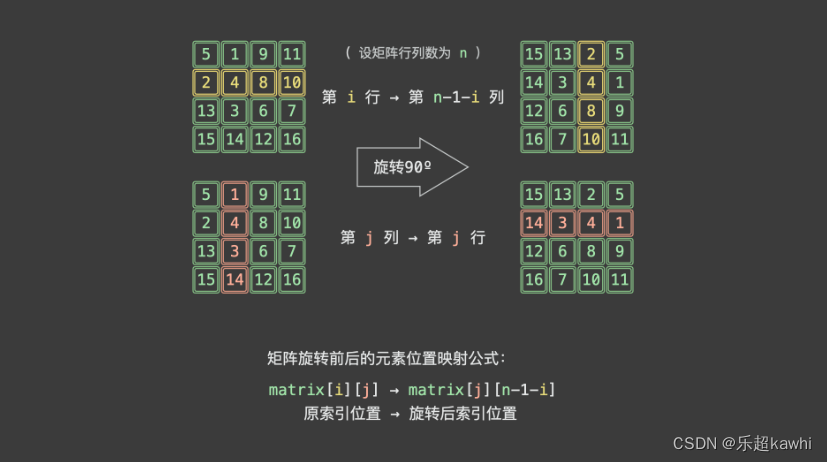
根据以上「元素旋转公式」,考虑遍历矩阵,将各元素依次写入到旋转后的索引位置。但仍存在问题:在写入一个元素 matrix[i][j]→matrix[j][n−1−i]后,原矩阵元素 matrix[j][n−1−i]就会被覆盖(即丢失),而此丢失的元素就无法被写入到旋转后的索引位置了。
为解决此问题,考虑借助一个「辅助矩阵」暂存原矩阵,通过遍历辅助矩阵所有元素,将各元素填入「原矩阵」旋转后的新索引位置即可。
代码:
1)代码:
void rotate(int** matrix, int matrixSize, int* matrixColSize) {
int n=matrixSize;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {#对角线互换
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
for(int i =0;i<n;i++){
int left=0,right=n-1;
while(left<right){#逐行交换
int temp = matrix[i][left];
matrix[i][left] = matrix[i][right];
matrix[i][right] = temp;
left++;
right--;
}
}
}2)代码:
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
# 深拷贝 matrix -> tmp
tmp = copy.deepcopy(matrix)
# 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素
for i in range(n):
for j in range(n):
matrix[j][n - 1 - i] = tmp[i][j]
作者:Krahets
链接:https://leetcode.cn/problems/rotate-image/solutions/1228078/48-xuan-zhuan-tu-xiang-fu-zhu-ju-zhen-yu-jobi/
来源:力扣(LeetCode)4.240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-10^9 <= matrix[i][j] <= 10^9- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-10^9 <= target <= 10^9
思路:
1)根据二分搜索,逐行确定可能范围列,然后在下一行进行搜索。
2)该算法作者:Krahets
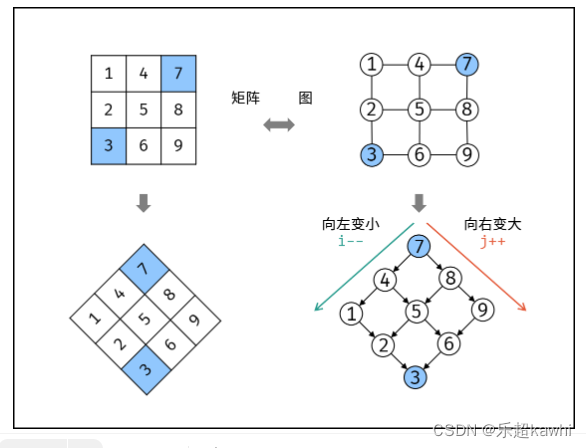
“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素,本文称之为 标志数 ,以 matrix 中的 左下角元素 为标志数 flag ,则有:
若 flag > target ,则 target 一定在 flag 所在 行的上方 ,即 flag 所在行可被消去。
若 flag < target ,则 target 一定在 flag 所在 列的右方 ,即 flag 所在列可被消去。从矩阵 matrix 左下角元素(索引设为 (i, j) )开始遍历,并与目标值对比:
当 matrix[i][j] > target 时,执行 i-- ,即消去第 i 行元素。
当 matrix[i][j] < target 时,执行 j++ ,即消去第 j 列元素。
当 matrix[i][j] = target 时,返回 truetruetrue ,代表找到目标值。
若行索引或列索引越界,则代表矩阵中无目标值,返回 falsefalsefalse 。
每轮 i 或 j 移动后,相当于生成了“消去一行(列)的新矩阵”, 索引(i,j) 指向新矩阵的左下角元素(标志数),因此可重复使用以上性质消去行(列)。
代码:
1)二分逐行查找发法
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0 || matrix[0].length == 0) {
return false;
}
for (int i = 0; i < matrix.length; i++) {
if (matrix[i][0] > target) {
break;
}
if(matrix[i][matrix[i].length - 1] < target){
continue;
}
int col = binarySearch(matrix[i], target);
if (col != -1) {
return true;
}
}
return false;
}
//二分查找
private int binarySearch(int[] nums, int target) {
int start = 0;
int end = nums.length - 1;
while (start <= end) {
int mid = (start + end) >>> 1;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
start = mid + 1;
} else {
end = mid - 1;
}
}
return -1;
}
2)
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
i, j = len(matrix) - 1, 0
while i >= 0 and j < len(matrix[0]):
if matrix[i][j] > target: i -= 1
elif matrix[i][j] < target: j += 1
else: return True
return False