一个序列的 宽度 定义为该序列中最大元素和最小元素的差值。

给你一个整数数组 nums ，返回 nums 的所有非空 子序列 的 宽度之和 。由于答案可能非常大，请返回对 109 + 7 取余 后的结果。

子序列 定义为从一个数组里删除一些（或者不删除）元素，但不改变剩下元素的顺序得到的数组。例如，[3,6,2,7] 就是数组 [0,3,1,6,2,2,7] 的一个子序列。

 

示例 1：

输入：nums = [2,1,3]
输出：6
解释：子序列为 [1], [2], [3], [2,1], [2,3], [1,3], [2,1,3] 。
相应的宽度是 0, 0, 0, 1, 1, 2, 2 。
宽度之和是 6 。

示例 2：

输入：nums = [2]
输出：0

 

提示：

    1 <= nums.length <= 105
    1 <= nums[i] <= 105

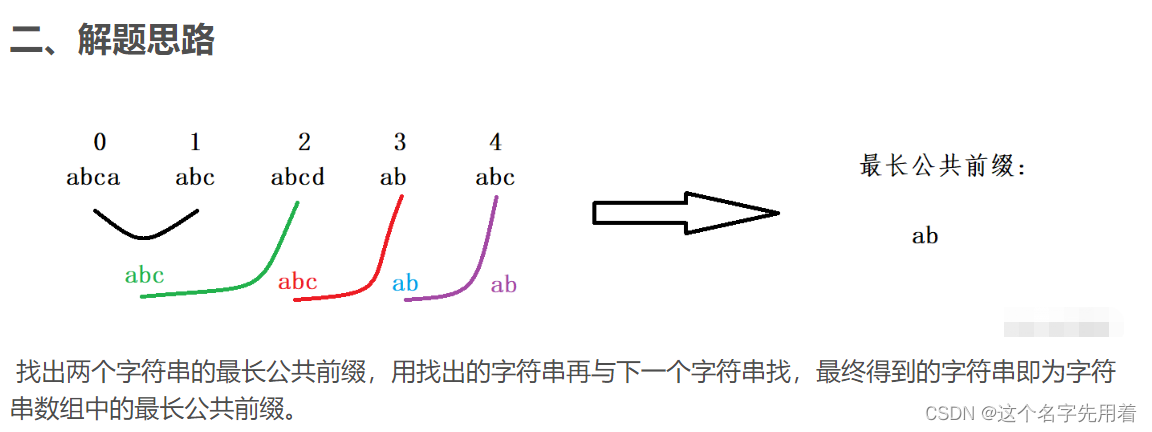
• 首先，宽度定义为该序列中最大元素和最小元素的差值。那么将任何子序列排序后的结果并不影响其宽度，因此我们将数组排序后也不影响答案的计算。
  

  通过上述推导，我们可以得出表格中的宽度计算值。
  通过观察发现，对于某个数nums[i]，我们统计其在宽度计算时出现的情况即可，会加上nums[i]:$1+2+4+...+2^{i-1}=2^i-1$次，会减去$2^{n-i-1}-1$次
  那么对于某个数nums[i]来说，它对宽度的贡献为：$(2^i)\ast nums[i]-nums[i]\ast (2^{n-i-1}-1)=nums[i]\ast (2^i-2^{n-i-1})$
  对于$2^i$，可以利用数组提前计算。
  最后，我们循环遍历每一个数统计其宽度的累加值即可。

• 时间复杂度：$O(nlogn)$

• 空间复杂度：$O(n)$

class Solution {
    public int sumSubseqWidths(int[] nums) {
        int n = nums.length, et = n - 1, st = 0, mod =(int)(1e9 + 7);
        long[] pow = new long[n + 5];
        long ans = 0, last = 1;
        Arrays.sort(nums);
        for (int i = 0; i <= n; i++) {
            pow[i] = last - 1;
            last = last * 2 % mod;
        }
        for (int i = 0; i < n; i++, st++, et--)  ans = (ans + (pow[st] - pow[et]) * nums[i]) % mod;
        return (int) ans;
    } 
}

• 空间优化：$O(long)$,为排序所需要的空间
• 我们使用一个变量来保存$2^i$的结果，对于第一个数来说是$2^0-2^{n-1}$, 对于最后一个数来说是$2^{n-1}-2^0$，那么每次计算宽度值的时候算第i个数和第n-i-1个数，即$(nums[i]-nums[n-i-1])\ast pow$

class Solution {
    public int sumSubseqWidths(int[] nums) {
        int n = nums.length, mod =(int)(1e9 + 7); 
        long ans = 0, pow = 1;
        Arrays.sort(nums);
        for (int i = 0; i < n; i++, pow = (pow * 2) % mod) ans = (ans + pow * (nums[i]  - nums[n - i - 1])) % mod;
        return (int) ans;
    } 
}