目录

一、介绍

二、简单点目标 RCS

三、复杂目标RCS

四、四个散射体组成的目标进行建模

五、具有多个散射体的扩展目标的宽带RCS

六、波动目标RCS

七、偏振目标RCS

八、结论

九、程序

---

此示例演示如何以不断提高的保真度对雷达目标进行建模。该示例介绍了简单点目标的雷达横截面 （RCS） 概念，并将其扩展到具有多个散射中心的目标的更复杂的情况。它还讨论了如何模拟RCS随时间推移的波动，并简要考虑了极化信号的情况。

一、介绍

雷达系统依靠目标反射或散射来检测和识别目标。目标反射越强，雷达接收器返回的回波就越大，从而获得更高的信噪比（SNR）和更高的检测可能性。在雷达系统中，从目标反射的能量由雷达横截面（RCS）决定，定义为

sigma代表RCS，R是雷达与目标之间的距离，Es是从目标反射的信号的场强，以及Ei是入射到目标上的信号的场强。通常，目标向各个方向散射能量，RCS是入射角，散射角和信号频率的函数。RCS 取决于目标的形状和构建目标的材料。用于RCS的常用单位包括平方米或dBsm。 本示例侧重于发射器和接收器位于同一位置时的窄带单基地雷达系统。入射角和散射角相等，RCS 仅是入射角的函数。这是反向散射的情况。对于窄带雷达，与工作频率相比，信号带宽很小，因此被认为是恒定的。

二、简单点目标 RCS

最简单的目标模型是各向同性散射体。各向同性散射体的一个例子是密度均匀的金属球体。在这种情况下，反射能量与入射角无关。各向同性散射体通常可以作为远离雷达的更复杂点目标的一阶近似。例如，行人可以用具有 1 平方米 RCS 的各向同性散射体近似。其中传播速度和雷达系统的工作频率。

三、复杂目标RCS

对于形状更复杂的目标，反射在所有方向上都不再被认为是相同的。RCS 随入射角（也称为纵横角）而变化。可以像测量天线辐射方向图一样测量或建模与方面相关的RCS方向图。此类测量或模型的结果是 RCS 值表，作为目标局部坐标系中方位角和仰角的函数。 下面的示例首先计算半径为 1 米、高度为 10 米的圆柱形目标的 RCS 模式，作为方位角和仰角的函数。

 

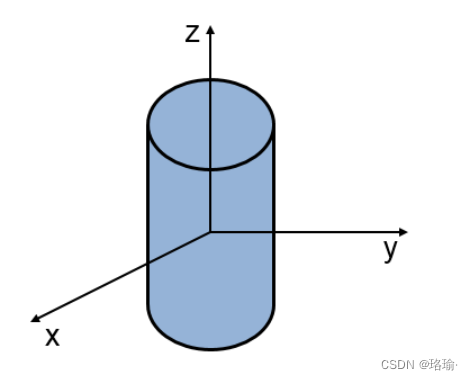
由于圆柱体围绕 z 轴对称，因此不存在方位角依赖关系。RCS 值仅随仰角而变化。

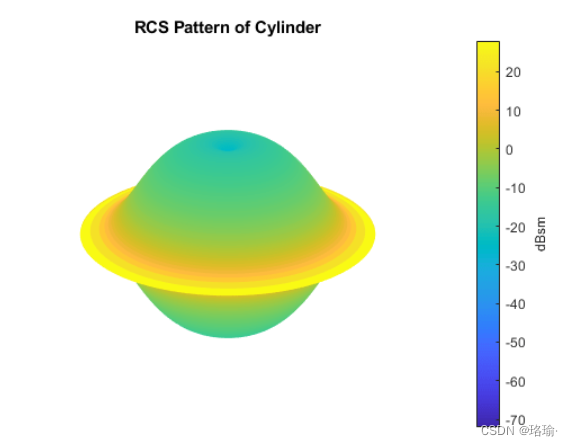
高程切口中的图案如下所示 

然后，可以将与方面相关的 RCS 模式导入到对象中。最后，生成目标反射。假设三个相等的信号从目标以三个不同的角度反射。前两个角度具有相同的仰角，但具有不同的方位角。最后一个与前两个具有不同的仰角。 

可以验证没有方位角依赖性，因为前两个输出是相同的。 存在分析派生的 RCS 模式的目标形状数量很少。对于更复杂的形状和材料，计算电磁学方法，如矩法（MoM）或有限元分析（FEM），可用于准确预测RCS模式。

四、四个散射体组成的目标进行建模

散射体位于正方形的四个顶点处。每个散射体都是上一节中派生的圆柱点目标。在不损失一般性的情况下，将正方形放置在xy 平面中。正方形的边长为0.5米。 

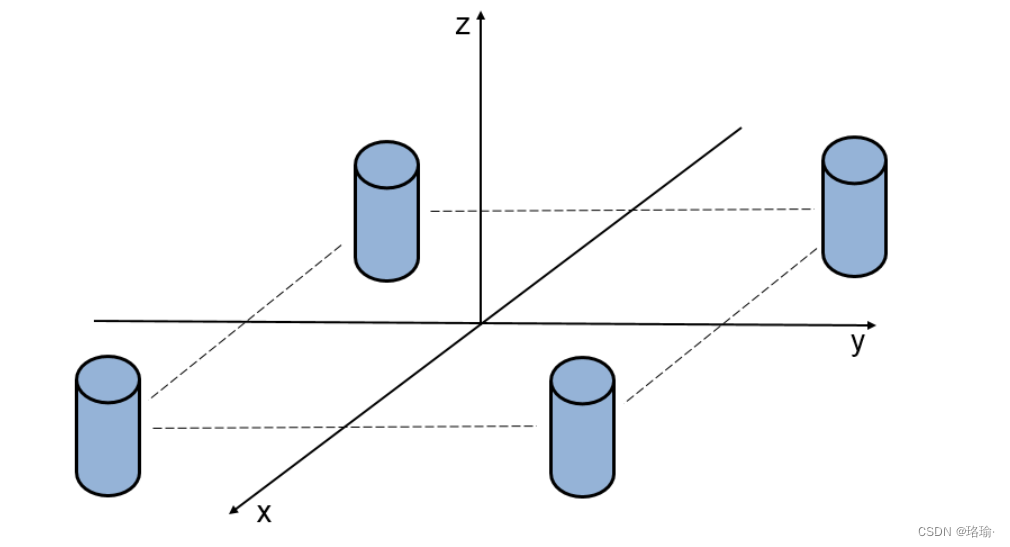
 首先，定义散射体的位置。如果目标在发射器的远场中，则每个分量散射体的入射角相同。

然后可以在对象中使用此模式来计算反射信号。结果验证了反射信号取决于方位角和仰角。 

五、具有多个散射体的扩展目标的宽带RCS

宽带雷达系统通常被定义为带宽大于其中心频率的5%。除了提高距离分辨率外，宽带系统还提供改进的目标检测。宽带系统提高检测性能的一种方法是在目标的RCS模式中填充淡入淡出。这可以通过重新访问由上一节中使用的4个圆柱形散射体组成的扩展目标来证明。扫描各个目标方面的建模窄带RCS如下所示：

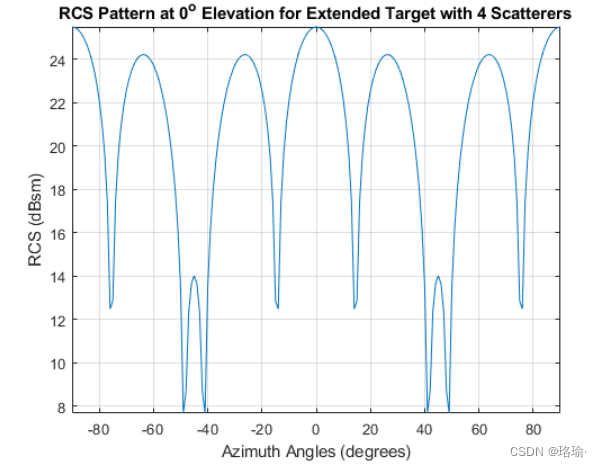
 扩展目标模型中多个圆柱体的回波连贯地组合在一起，在 40 到 50 度之间产生深淡入淡出。这些淡入淡出会导致雷达传感器无法检测到目标。 接下来，将检查在相同中心频率下工作的宽带系统的RCS模式。该系统的带宽将设置为中心频率的10%

创建宽带 RCS 模型，就像之前为窄带扩展目标所做的那样。通常，RCS模型是使用仿真工具或距离测量离线生成的，然后提供给雷达工程师用于其系统模型。在这里，假设提供的RCS模型已在雷达中心频率的两侧以1MHz的间隔进行采样。

来自各种散射中心的贡献像以前一样建模。需要注意的是，这种近似假设所有目标的散射中心都落在相同的距离分辨率箱内，对于本例来说也是如此。

现在使用刚刚计算的 RCS 模式生成宽带 RCS 目标模型。现在可以将建模的宽带RCS与窄带系统进行比较。

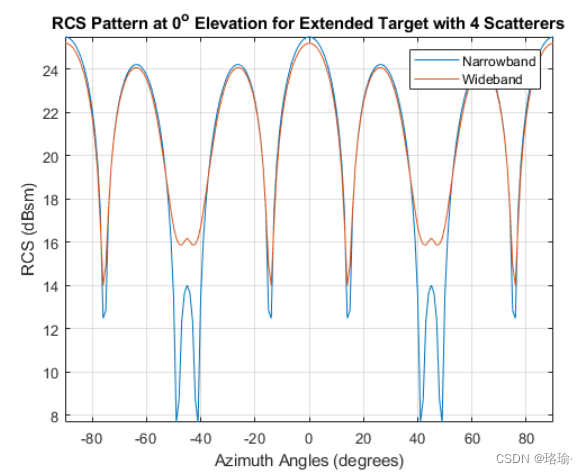
目标的RCS模式现在在40到50度方位角之间具有更浅的零点。当信号以特定频率和方位角组合破坏性组合时，就会出现窄带模式中的深度零点。宽带波形填充这些淡入淡出，因为虽然某些频率在给定方面可能会出现零点，但大部分带宽在该方位角处不在零点内。 

六、波动目标RCS

到目前为止的讨论假设目标 RCS 值随时间变化是恒定的。这是非波动的目标情况。实际上，由于雷达系统和目标都在移动，因此RCS值会随着时间的推移而变化。这种情况是一个波动的目标。为了模拟波动的目标，Peter Swerling开发了四个统计模型，称为Swerling 1到Swerling 4，在实践中被广泛采用。Swerling 模型将波动目标分为两个概率分布和两个时变行为，如下表所示：

缓慢波动目标的RCS在停留期间保持不变，但因扫描而异。相比之下，快速波动目标的RCS随停留内的每个脉冲而变化。 

Swerling 1 和 2 模型遵循指数密度函数 （pdf） 

 Swerling 3 和 4 模型遵循 4 度卡方 pdf

 在 Swerling 1 案例中，反射不再是恒定的。RCS 值因扫描而异。假设每个停留仅由信号照射一次目标，则以下代码模拟单元入射信号的 10，000 次扫描的反射信号功率。

绘制所有扫描的回报直方图，并验证返回的分布是否与理论预测匹配。理论预测使用之前推导的非波动RCS。

七、偏振目标RCS

目标RCS也是极化的函数。要描述目标的偏振特征，单个RCS值已不再足够。相反，对于每个频率和入射角，散射矩阵用于描述目标与输入信号的偏振分量的相互作用。

八、结论

本例简要介绍了雷达系统仿真的雷达目标建模。它展示了如何对点目标、具有测量模式的目标和扩展目标进行建模。它还描述了在生成目标回波时如何考虑统计波动。

九、程序

使用Matlab R2022b版本，点击打开。

 打开下面的“TargetRCSExample.m”文件，点击运行，就可以看到上述效果。

 

关注下面公众号，后台回复关键词：目标雷达横截面建模，发送源码链接。