1.1 K-近邻算法简介
1.定义:
就是通过你的"邻居"来判断你属于哪个类别
2.如何计算你到你的"邻居"的举例
一般时候,都是使用欧氏距离
1.2k近邻算法api初步使用
1.sklearn
优势:
1.文档多,且规范,
2.包含的算法多
3.实现起来容易
2.sklearn中包含内容
分类、聚类、回归特征工程
模型选择、调优
3.knn中的api
sklearn.neighbors .KNeighborsClassifier(n_neighbors=5)
参数:
n_beighbors --选定参考几个邻居
4.机器学习中实现的过程
1.实例化一个估计器
2.使用fit方法进行训练
1.3距离度量
1.欧式距离
通过距离平方值进行计算

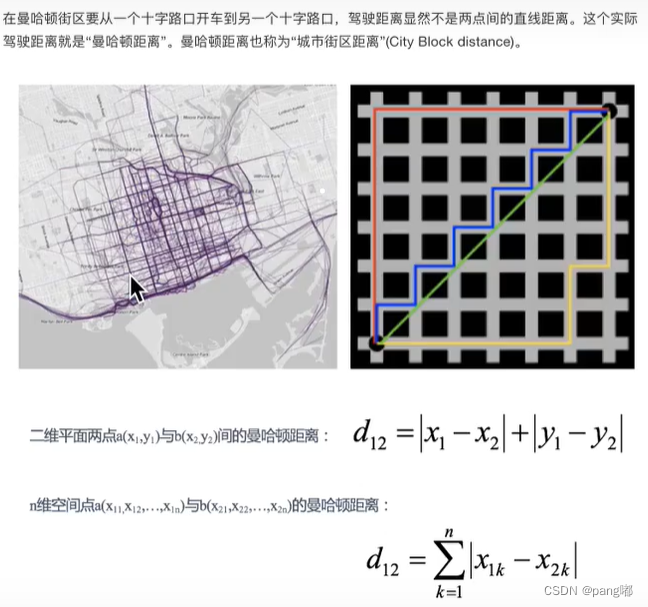
2.曼哈顿距离(Manhattan Distance):
通过举例的绝对值进行计算
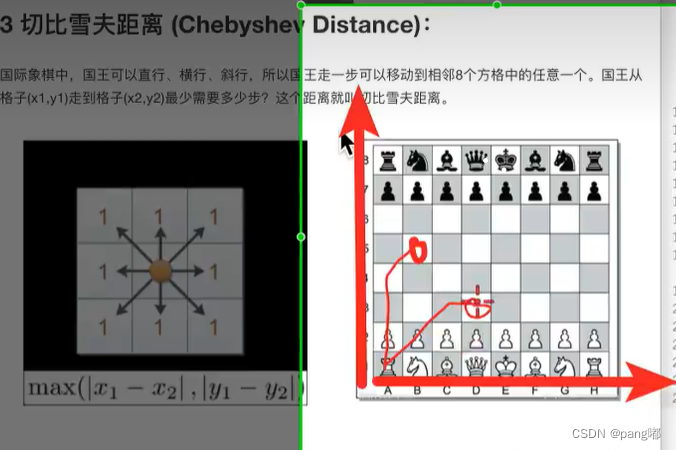
3.切比雪夫距离(Chebyshev Distance):
维度的最大值进行计算

4.颍可夫斯基距离(Minkowski Distance):
当p=1时,就是曼哈顿距离;
当p=2时,就是欧氏距离;当p-~时,就是切比雪夫距离。
小结:前面四个距离公式都是把单位相同看待了,所以计算过程不是很科学

5.标准化欧氏距离(StandardizedEuclideanDistance) :
在计算过程中添加了标准差,对量刚数据进行处理

6.余弦距离(Cosine Distance)
通过cos思想完成
7.汉明距离( Hamming Distance)【了解】∶
一个字符串到另一个字符串需要变换几个字母,进行统计
8.杰卡德距离(Jaccard Distance)【了解】∶
通过交并集进行统计
9.马氏距离(Mahalanobis Distance)【了解】
通过样本分布进行计算
1.4 k值选择
k值过小: 容易受到异常点的影响过拟合
k值过大: 受到样本均衡的问题欠拟合
拓展:
近似误差--过拟合 --在训练集上表现好,测试集表现不好
估计误差好才是真的好!
1.5 kd树
1.构建树
2.最近领域搜索
案例:
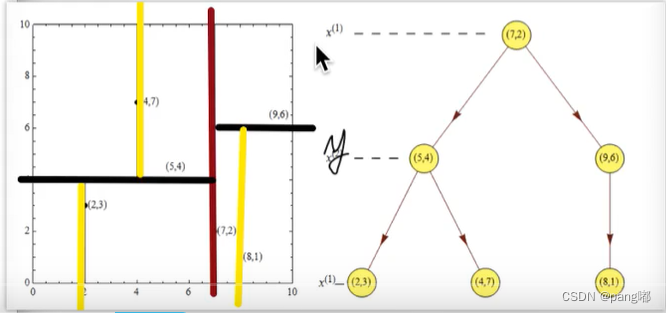
—,构建树
第一次:
×轴--2,5,9,4,8,7 --> 2,4,5,7,8,9
y轴--3,4,6,7,1,2 --> l,2,3,4,6,7
首先选择x轴,找中间点,发现是(7,2)
第二次:
左面:(2,3), [ 4,7],[5,4 ] --> 3,4,7
右面:(8,1) , (9,6)--> 1,6
从y轴开始选择,
左边选择点是(5,4), 右边选择点(9,6)
第三次:
从x轴开始选择
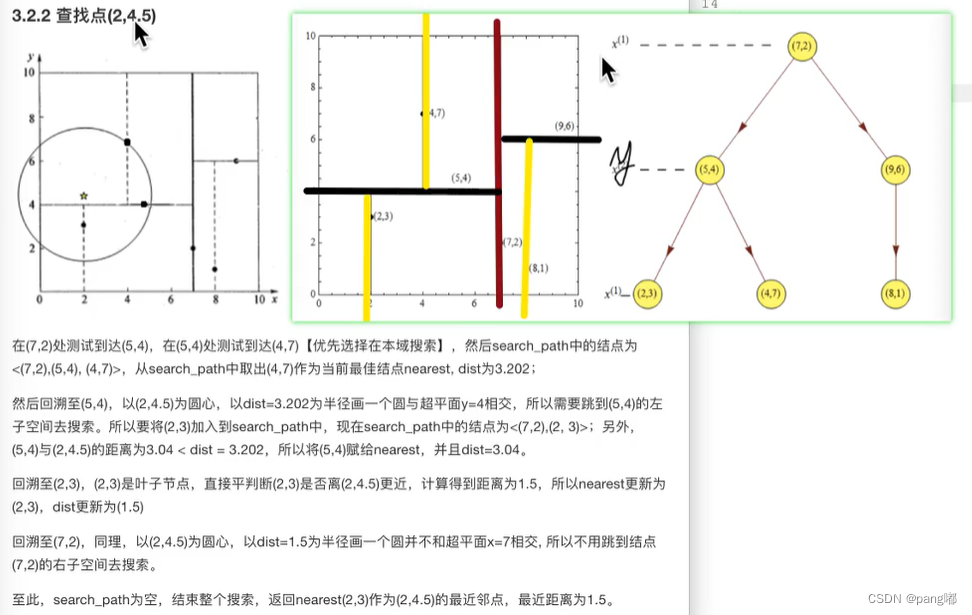
二,搜索
1.在本域内,没有进行跨域搜索

2.要跨到其他域搜索
1.6案例:鸢尾花种类预测--数据集介绍
1.获取数据集
sklearn . datasets.
小数据:
sklearn . datasets . load_*
注意:该数据从本地获取
大数据集:
sklearn.datasets. fetch_*
注意: 该数据从网上下载
subset--表示获取到的数据集类型
2.数据集返回值介绍
返回值类型是bunch--是一个字典类型
返回值的属性:
data︰特征数据数组,是In_samples * n_features]的二维 numpy.ndarray 数组
target︰标签数组,是n_samples的一维numpy.ndarray数组
DESCR:数据描述
feature_names:特征名,新闻数据,手写数字、回归数据集没有
target_names:标签名