堆是其中一种非常重要且实用的数据结构。堆可以用于实现优先队列,进行堆排序,以及解决各种与查找和排序相关的问题。本文将深入探讨两种常见的堆结构:大顶堆和小顶堆,并通过 C++ 语言展示如何实现和使用它们。
一、定义
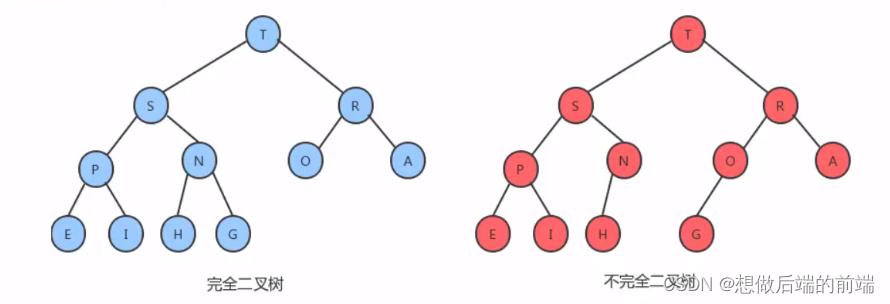
堆是一种完全二叉树。完全二叉树的定义:所有节点从上往下,从左往右的依次排列,不能有空位置,是为完全二叉树。
下面是完全二叉树和不完全二叉树的示意图:
大顶堆:
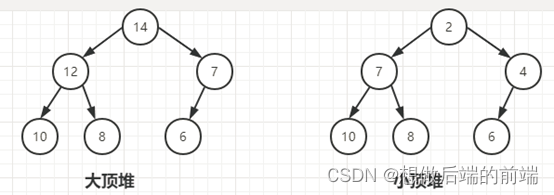
根节点(堆顶元素)是所有节点中的最大值(父节点都大于左右子节点)。大顶堆常用于实现优先队列,且可用于构建堆排序算法。
小顶堆:
小顶堆中的根节点是所有节点中的最小值(父节点都小于左右子节点)。小顶堆常用于问题如:查找流中的前 K 个最小元素。
二、实现
通常用 数组 来实现:具体方法就是将二叉树的结点按照 层级顺序 放入数组中, 根结点在 位置1(数组索引0处不存储数据),它的子结点在位置2和3,而子结点的子结点则分别在位置4,5,6和7,以此类推
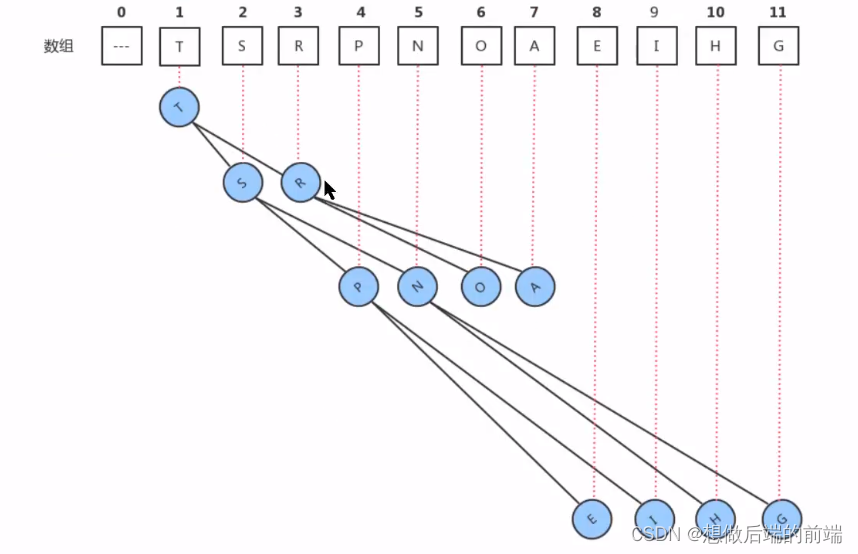
- 如果一个结点的位置为 k,则它的父结点的位置为 k/2
- 两个子结点的位置则分别为 2k 和 2k+1
2.1 Insert
堆是用 数组 完成数据元素的存储的,由于数组的底层是一串连续的内存地址,所以要往堆中插入数据,只能往数组中从索引0处开始,依次往后存放数据,但是堆中对元素的顺序是有要求的,每一个结点的数据要 大于等于它的两个子结点的数据,所以每次插入一个元素,都会使得堆中的数据顺序变乱,这个时候就需要通过一些方法,让刚才插入的这个数据放入到合适的位置
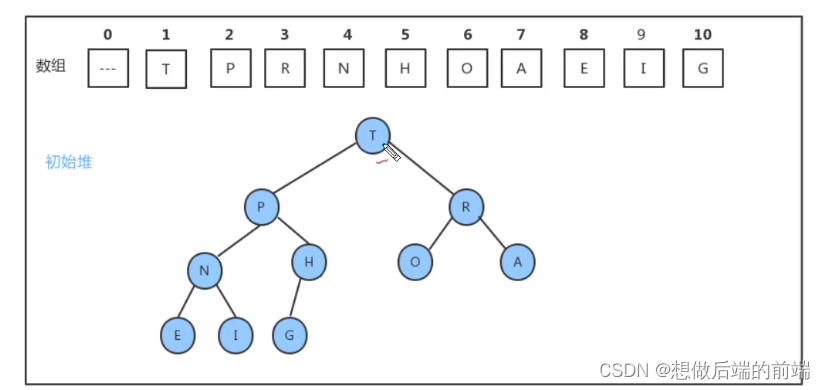
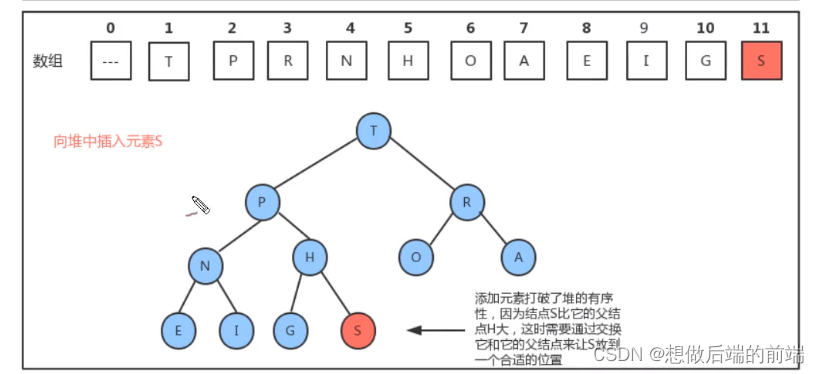
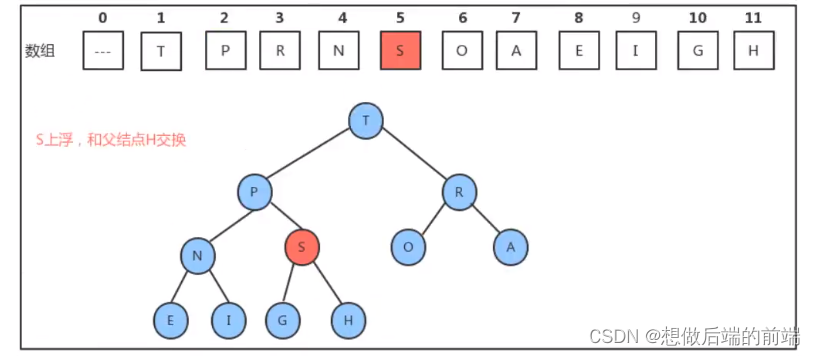
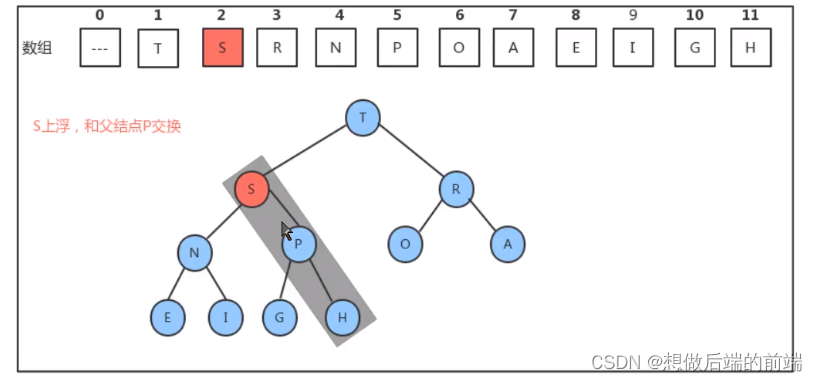
所以,如果往堆中新插入元素,只需要不断的比较新结点 a[k] 和它的父结点 a[k/2] 的大小,然后根据结果完成数据元素的交换,就可以完成堆的有序调整。
2.1 delMax
由大顶堆的特性可以知道,索引1处的元素,也就是根结点就 是最大的元素,把根结点的元素删除后,需要有一个新的根结点出现,这时可以 暂时把堆中最后一个元素放到索引1处,充当根结点,但是它有可能不满足堆的有序性需求,这个时候就需要通过一些方法,让这个新的根结点放入到合适的位置
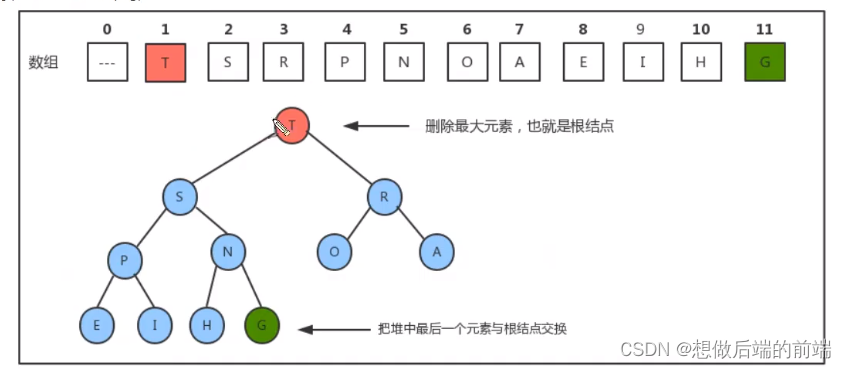
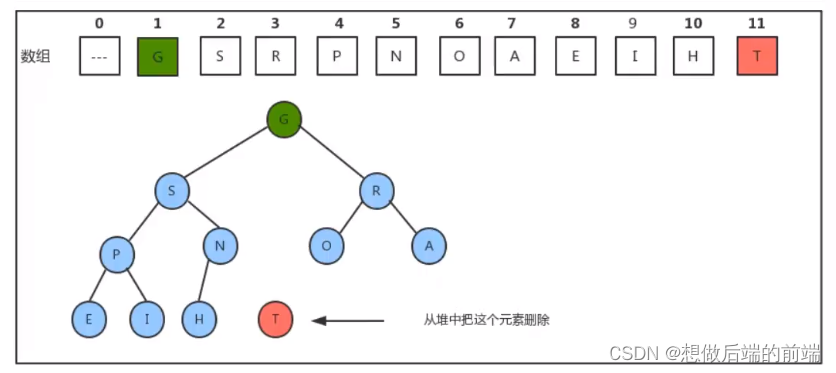

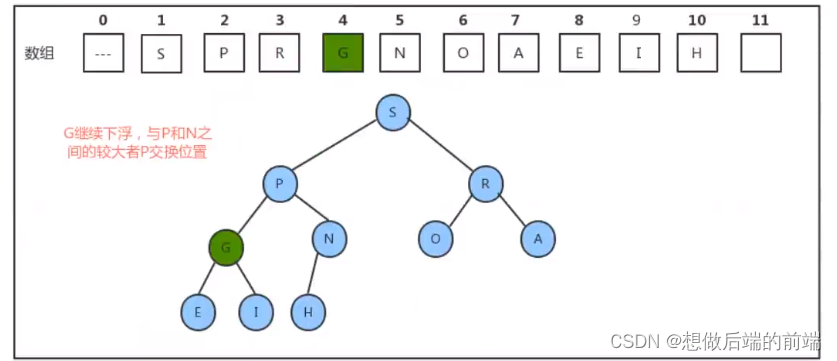

所以,当删除掉最大元素后,只需要将最后一个元素放到索引1处,并不断的拿着当前结点 a[k] 与它的子结点a[2k] 和 a[2k+1] 中的较大者交换位置,即可完成堆的有序调整。
三、堆排序
要求:给你一个数组 {4,6,8,5,9} , 要求使用堆排序法,将数组升序排序。
实现步骤:
- 构造堆
- 得到堆顶元素,这个值就是最大值
- 交换堆顶元素和数组中的最后一个元素,此时所有元素中的最大元素已经放到合适的位置
- 对堆进行调整,重新让除了最后一个元素的剩余元素中的最大值放到堆顶
- 重复2~4这个步骤,直到堆中剩一个元素为止
3.1 堆构造过程
堆的构造,最直观的想法就是另外再创建一个新数组,然后从左往右遍历原数组,每得到一个元素后,添加
到新数组中,并通过上浮,对堆进行调整,最后新的数组就是一个堆
上述的方式虽然很直观,也很简单,但是可以用更聪明一点的办法完成它
创建一个新数组,把原数组0 ~ length-1的数据拷贝到新数组的 1 ~ length 处,再从新数组 长度的一半 处开始往 1索引 处扫描(从右往左),然后对扫描到的每一个元素做下沉调整即可
为什么是新数组长度的一半?
因为新数组是一个无序堆,长度的一半之后的结点为叶子结点;叶子结点不需要要下沉调整
1.假设给定无序序列结构如下:
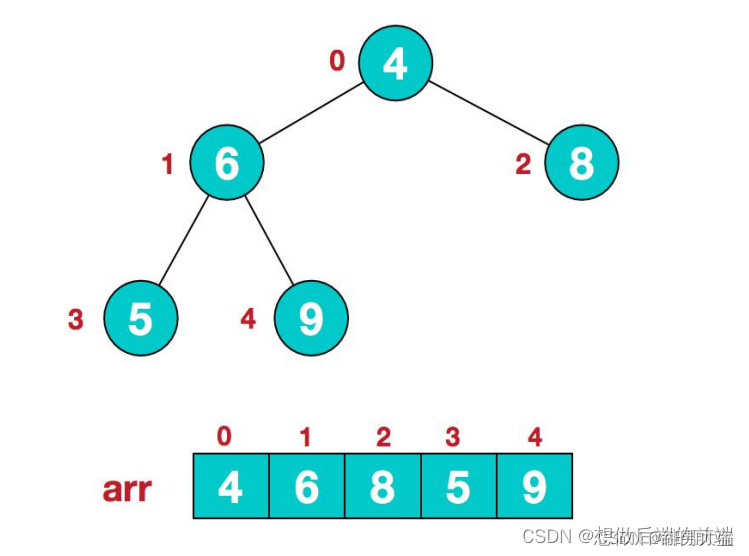
2.此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。
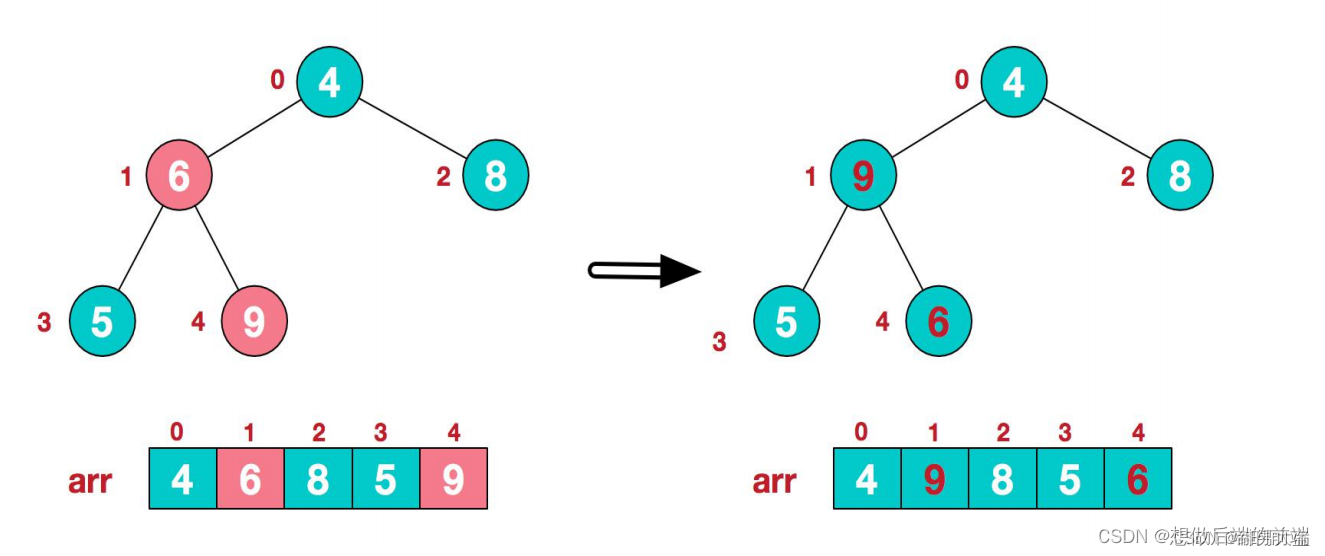
3.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
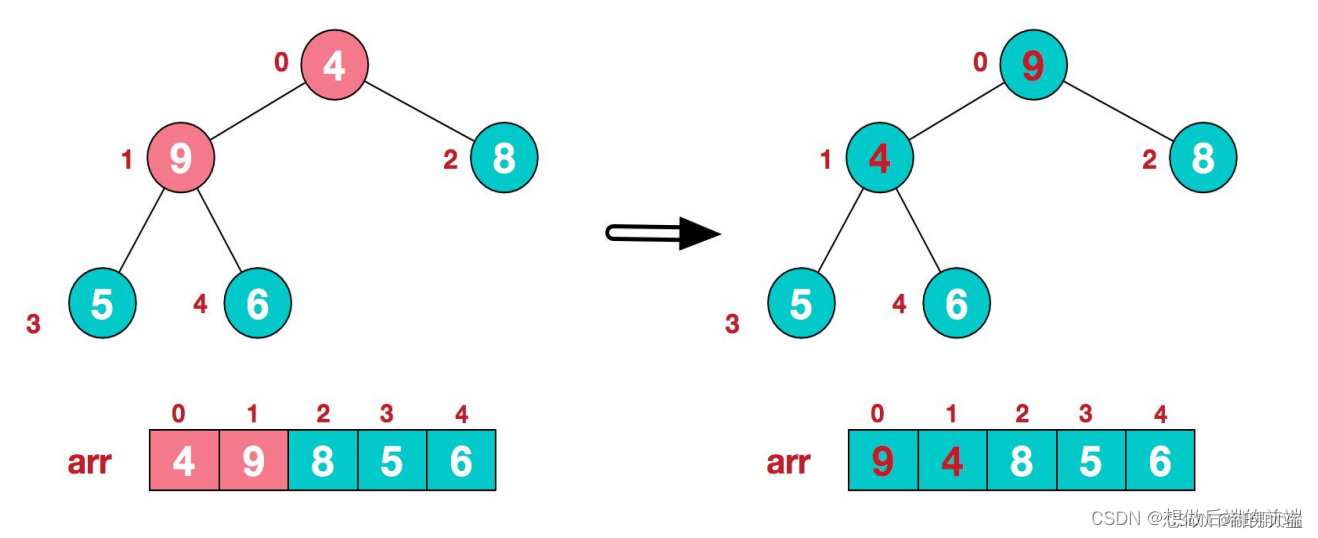
4.这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。

3.2 堆排序过程
对构造好的堆,只需要做 类似于堆的删除操作,就可以完成排序:
- 将堆顶元素和堆中最后一个元素交换位置
- 通过对堆顶元素下沉调整堆,把最大的元素放到堆顶 (此时最后一个元素不参与堆的调整,因为最大的数据已经到了数组的最右边)
- 重复1~2步骤,直到堆中剩最后一个元素
1.将堆顶元素9和末尾元素4进行交换
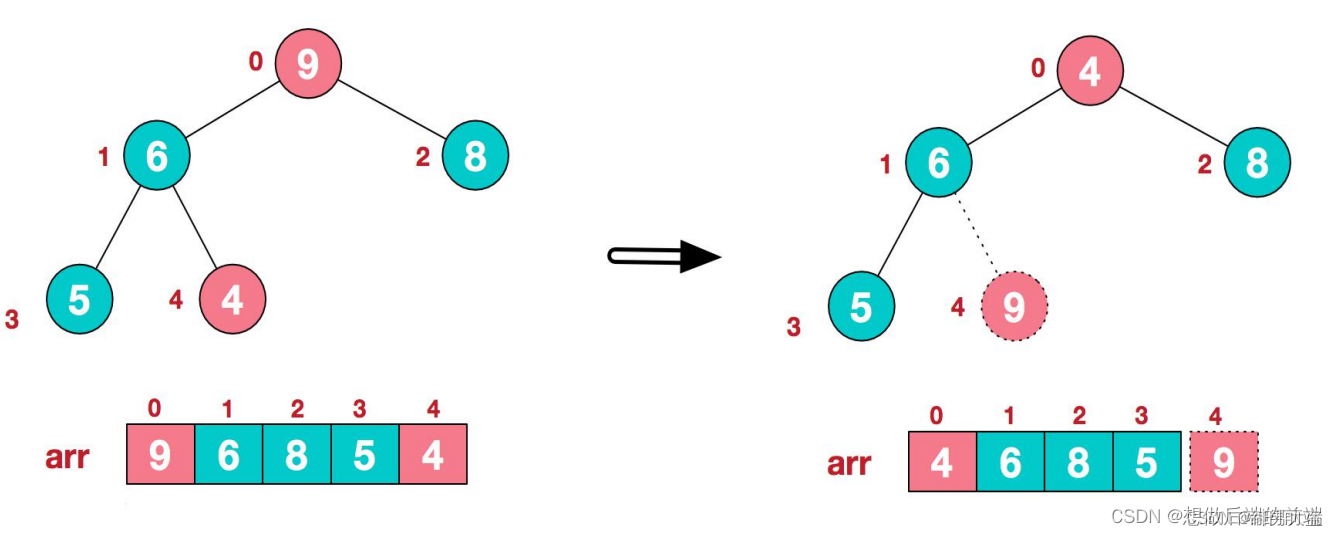
2.重新调整结构,使其继续满足堆定义
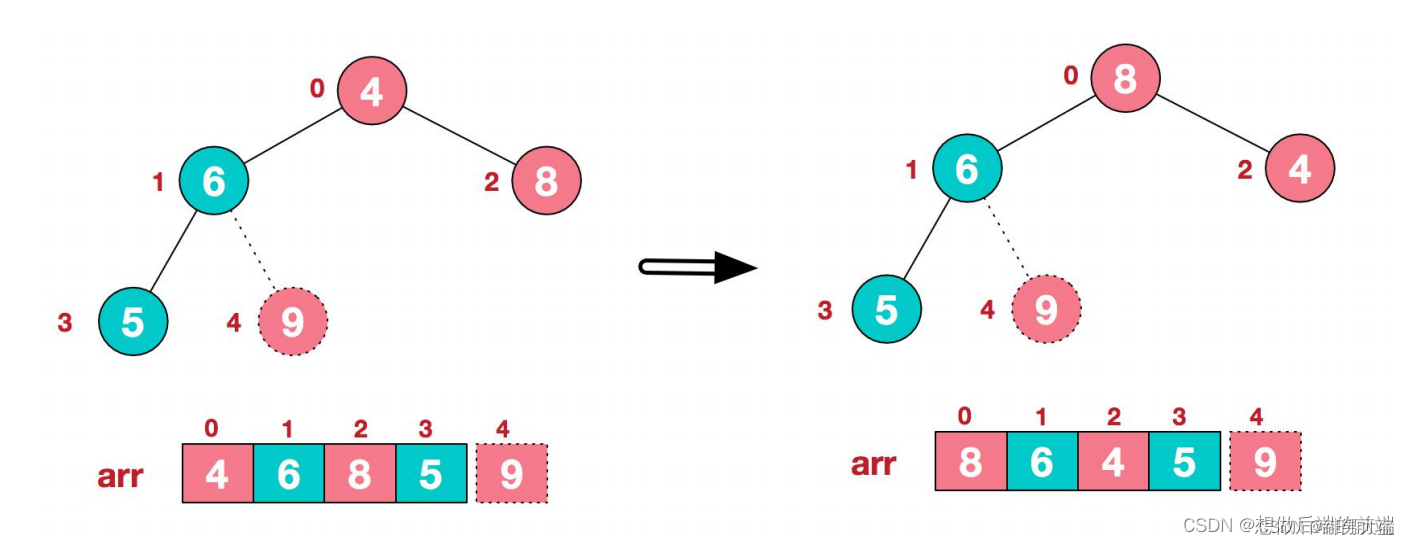
3.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8
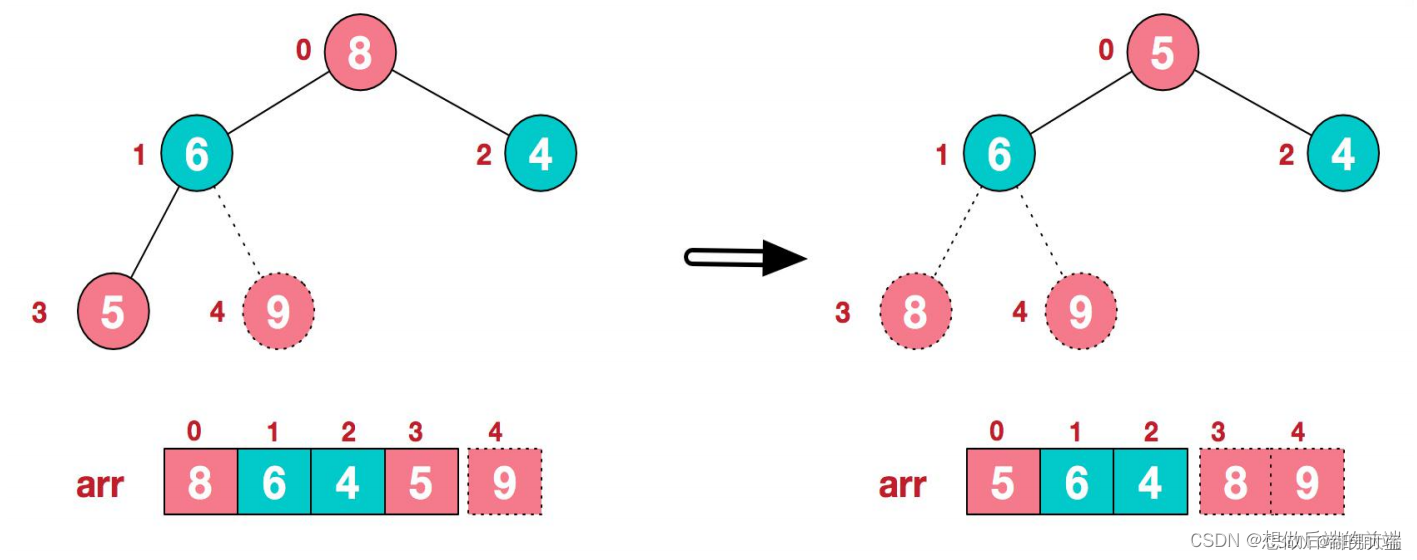
4.后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序

3.3 总结堆排序的基本思路
1).将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端:
3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤
直到整个序列有序。
至于完整的代码实现和动画显示,可以参考我的文章 - 排序算法基础