06 单目初始化器 Initializer

单目 SLAM 初始化相关，双目和 RGBD 不会使用这个类。

单目相机运动得到两帧图像，调用该类，当满足一定条件时认为初始化成功，否则重新初始化。

6.1 成员变量/函数

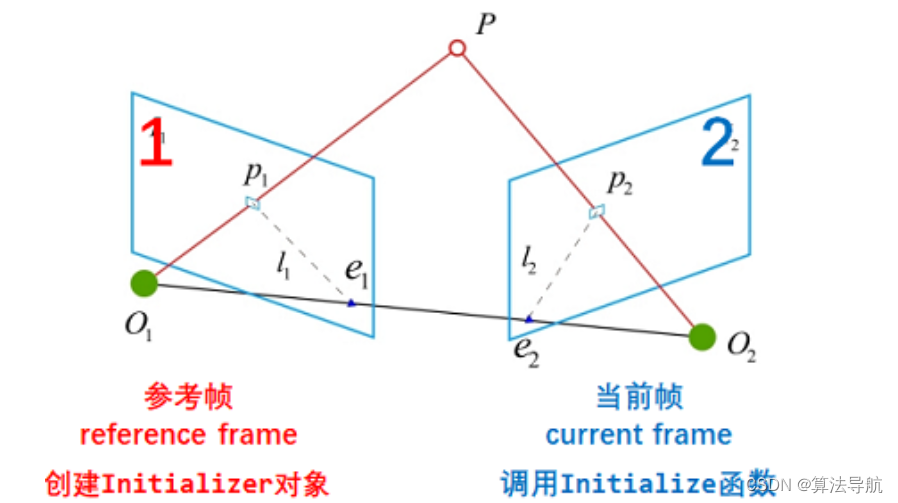
用 reference frame 来初始化，这个 reference frame 就是 SLAM 正式开始的第一帧；用 current frame，也就是用 SLAM 逻辑上的第二帧来初始化整个 SLAM，得到最开始两帧之间的 $\mathbf{R}$、 $\mathbf{t}$，以及点云。

成员函数/变量	访问控制	意义
Initializer(...)	public	构造函数，用 reference frame 来初始化
bool Initialize(...)	public	用 current frame，得到最开始两帧之间的 $\mathbf{R}$、 $\mathbf{t}$，以及点云
vector<cv::KeyPoint> mvKeys1	private	存储 reference frame 中的特征点
vector<cv::KeyPoint> mvKeys2	private	存储 current frame 中的特征点
vector<Match> mvMatches12	private	记录 Reference 到 Current 匹配上的特征点对
vector<bool> mvbMatched1	private	记录 Reference Frame 的每个特征点在 Current Frame 是否有匹配的特征点
cv::Mat mK	private	相机内参
float mSigma, mSigma2	private	测量误差
int mMaxIterations	private	RANSAC 迭代次数
vector<vector<size_t> > mvSets	private	二维容器 $N\times 8$ 每一层保存 RANSAC 计算 H 和 F 矩阵所需的八对点

6.2 初始化函数 Initialize()

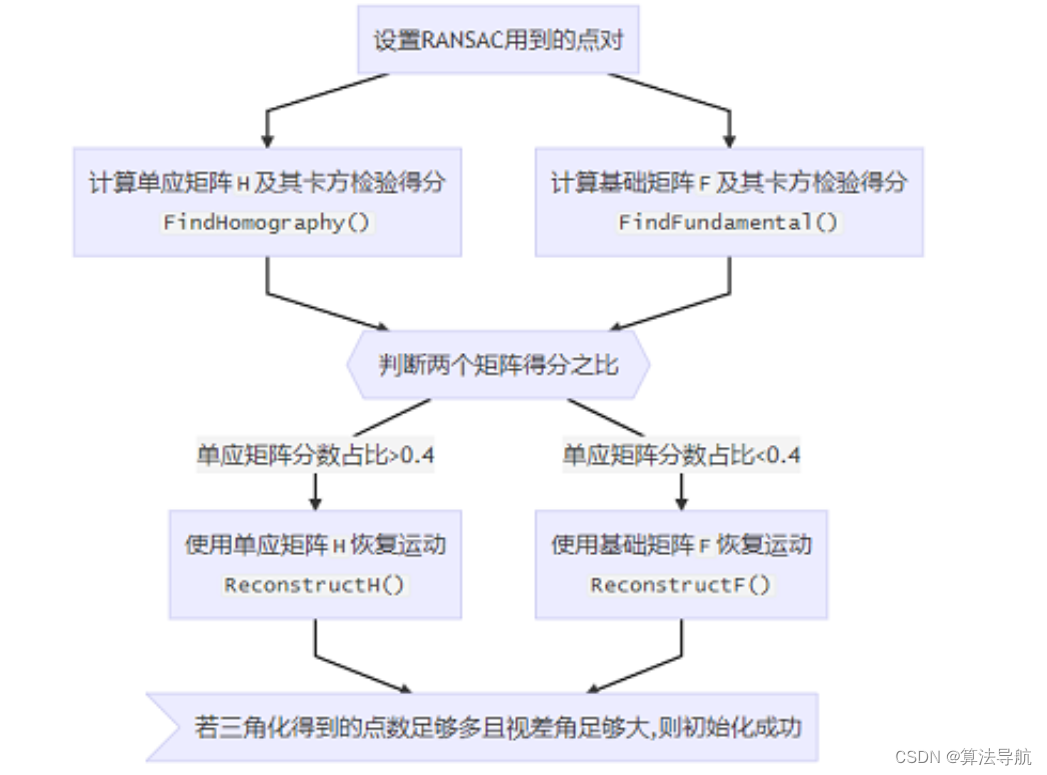
主函数 Initialize() 根据两帧间的匹配关系恢复帧间运动并计算地图点位姿。

6.3 计算基础矩阵 $\mathbf{F}$ 和单应矩阵 $\mathbf{H}$

6.3.1 RANSAC 算法

RANSAC 算法的核心是减少每次迭代所需的采样点数。从原理上来说,计算 $F$ 矩阵最少只需要 7 对匹配点，计算 $H$ 矩阵最少只需要 4 对匹配点。ORB-SLAM2 中为了编程方便，每次迭代使用 8 对匹配点计算 $F$ 和 $H$。

6.3.2 八点法计算 $\mathbf{F}$ 矩阵: ComputeF21()

对极约束

$${\mathbf{p}}_2^T\mathbf{F}{\mathbf{p}}_1=0$$

其中 ${\mathbf{p}}_1、{\mathbf{p}}_2$ 为对应特征点。

$$\left(u_2,v_2,1\right)\left(\begin{array}{lll}{\mathrm{f}}_{11}& {\mathrm{f}}_{12}& {\mathrm{f}}_{13}\\ {\mathrm{f}}_{21}& {\mathrm{f}}_{22}& {\mathrm{f}}_{23}\\ {\mathrm{f}}_{31}& {\mathrm{f}}_{32}& {\mathrm{f}}_{33}\end{array}\right)\left(\begin{array}{c}{\mathrm{u}}_1\\ {\mathrm{v}}_1\\ 1\end{array}\right)=0$$

为方便计算先展开前两项，并记为 $a、b、c$

$$\begin{array}{rl}& a=f_{11}\ast u_2+f_{21}\ast v_2+f_{31}\\ & b=f_{12}\ast u_2+f_{22}\ast v_2+f_{32}\\ & c=f_{13}\ast u_2+f_{23}\ast v_2+f_{33}\end{array}$$

则上面的矩阵可记为

$$\left[\begin{array}{lll}a& b& c\end{array}\right]\left[\begin{array}{c}{u}_1\\ v_1\\ 1\end{array}\right]=0$$
展开

$$a\ast u_1+b\ast v_1+c=0$$

代入 $a、b、c$

$${\mathrm{u}}_1{\mathrm{u}}_2{\mathrm{f}}_{11}+{\mathrm{u}}_1{\mathrm{v}}_2{\mathrm{f}}_{21}+{\mathrm{u}}_1{\mathrm{f}}_{31}+{\mathrm{v}}_1{\mathrm{u}}_2{\mathrm{f}}_{12}+{\mathrm{v}}_1{\mathrm{v}}_2{\mathrm{f}}_{22}+{\mathrm{v}}_1{\mathrm{f}}_{32}+{\mathrm{u}}_2{\mathrm{f}}_{13}+{\mathrm{v}}_2{\mathrm{f}}_{23}+{\mathrm{f}}_{33}=0$$

由于尺度不变性（可同时除 $f_{33}$），只有八个未知数，至少需要八对点

$$\left(\begin{array}{ccccccccc}{\mathrm{u}}_1^1{\mathrm{u}}_2^1& {\mathrm{u}}_1^1{\mathrm{v}}_2^1& {\mathrm{u}}_1^1& {\mathrm{v}}_1^1{\mathrm{u}}_2^1& {\mathrm{v}}_1^1{\mathrm{v}}_2^1& {\mathrm{v}}_1^1& {\mathrm{u}}_2^1& {\mathrm{v}}_2^1& 1\\ {\mathrm{u}}_1^2{\mathrm{u}}_2^2& {\mathrm{u}}_1^2{\mathrm{v}}_2^2& {\mathrm{u}}_1^2& {\mathrm{v}}_1^2{\mathrm{u}}_2^2& {\mathrm{v}}_1^2{\mathrm{v}}_2^2& {\mathrm{v}}_1^2& {\mathrm{u}}_2^2& {\mathrm{v}}_2^2& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ {\mathrm{u}}_1^8{\mathrm{u}}_2^8& {\mathrm{u}}_1^8{\mathrm{v}}_2^8& {\mathrm{u}}_1^8& {\mathrm{v}}_1^8{\mathrm{u}}_2^8& {\mathrm{v}}_1^8{\mathrm{v}}_2^8& {\mathrm{v}}_1^8& {\mathrm{u}}_2^8& {\mathrm{v}}_2^8& 1\end{array}\right)\left(\begin{array}{c}{\mathrm{f}}_{11}\\ {\mathrm{f}}_{12}\\ {\mathrm{f}}_{13}\\ {\mathrm{f}}_{21}\\ {\mathrm{f}}_{22}\\ {\mathrm{f}}_{23}\\ {\mathrm{f}}_{31}\\ {\mathrm{f}}_{32}\\ {\mathrm{f}}_{33}\end{array}\right)=0$$

使用 SVD 分解求出最小二乘解。

cv::Mat u,w,vt;

cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);

cv::Mat Fpre = vt.row(8).reshape(0, 3); // v的最后一列

cv::SVDecomp(Fpre,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);

w.at<float>(2)=0; // 秩2约束，将第3个奇异值设为0

return  u*cv::Mat::diag(w)*vt;

6.3.3 计算基础矩阵 $\mathbf{F}$ 及其得分：FindFundamental()

此函数主要流程为：

• 特征点归一化：Normalize()

• 调用函数 ComputeF21() 计算基础矩阵，采用 RANSAC 算法，找到评分（卡方检验）最高的解：ComputeH21()、CheckHomography()

6.3.4 计算 $\mathbf{H}$ 矩阵: ComputeH21()

若场景中的特征点都落在同一平面（墙、地面），则可以用单应矩阵进行运动估计。

$${\mathbf{p}}_2=\mathbf{H}{\mathbf{p}}_1$$

${\mathbf{p}}_1、{\mathbf{p}}_2$ 为对应特征点。

一般来说，4 对点即可求解

$$\left(\begin{array}{cccccccc}{u}_1^1& v_1^1& 1& 0& 0& 0& -u_1^1{u}_2^1& -v_1^1{u}_2^1\\ 0& 0& 0& u_1^1& v_1^1& 1& -u_1^1{v}_2^1& -v_1^1{v}_2^1\\ u_1^2& v_1^2& 1& 0& 0& 0& -u_1^2{u}_2^2& -v_1^2{u}_2^2\\ 0& 0& 0& u_1^2& v_1^2& 1& -u_1^2{v}_2^2& -v_1^2{v}_2^2\\ u_1^3& v_1^3& 1& 0& 0& 0& -u_1^3{u}_2^3& -v_1^3{u}_2^3\\ 0& 0& 0& u_1^3& v_1^3& 1& -u_1^3{v}_2^3& -v_1^3{v}_2^3\\ u_1^4& v_1^4& 1& 0& 0& 0& -u_1^4{u}_2^4& -v_1^4{u}_2^4\\ 0& 0& 0& u_1^4& v_1^4& 1& -u_1^4{v}_2^4& -v_1^4{v}_2^4\end{array}\right)\left(\begin{array}{c}{h}_1\\ h_2\\ h_3\\ h_4\\ h_5\\ h_6\\ h_7\\ h_8\end{array}\right)=\left(\begin{array}{c}{u}_2^1\\ v_2^1\\ u_2^2\\ v_2^2\\ u_2^3\\ v_2^3\\ u_2^4\\ v_2^4\end{array}\right).$$

这里为了和 ComputeH21() 一致，也采用八点法。通过 SVD 分解求出 $\mathbf{H}$ 矩阵。

6.3.5 计算单应矩阵 $\mathbf{H}$ 及其得分 FindHomography()

过程类似 FindFundamental()。

6.3.6 卡方检验计算置信度得分: CheckFundamental()、CheckHomography()

卡方检验通过构造检验统计量 $\chi$ 来比较期望结果和实际结果之间的差别，从而得出观察频数极值的发生概率。

$${\chi }^2=\Sigma \frac{(\mathrm{O}-\mathrm{E}{)}^2}{\mathrm{E}}$$

（1）CheckHomography()

计算重投影误差，也就是计算投影点与对应匹配点的像素距离的平方（计算值与真实值），作为卡方值。

有前面

$${\mathbf{p}}_2=\mathbf{H}{\mathbf{p}}_1$$

将帧 1 特征点左乘单应矩阵，得到帧 2 中对应特征点的计算值。反之，则为 ${\mathbf{p}}_1={\mathbf{H}}^{-1}{\mathbf{p}}_2$

// Reprojection error in second image
// x1in2 = H21*x1
// 将图像1中的特征点单应到图像2中
// |u1|   |h11 h12 h13||u2|
// |v1| = |h21 h22 h23||v2|
// |1 |   |h31 h32 h33||1 |
const float w1in2inv = 1.0/(h31*u1+h32*v1+h33);  
const float u1in2 = (h11*u1+h12*v1+h13)*w1in2inv;
const float v1in2 = (h21*u1+h22*v1+h23)*w1in2inv;

const float squareDist2 = (u2-u1in2)*(u2-u1in2)+(v2-v1in2)*(v2-v1in2);  // 计算平方误差

const float chiSquare2 = squareDist2*invSigmaSquare;  // 卡方

if(chiSquare2>th)
    bIn = false;
else
    score += th - chiSquare2;   // 得分

if(bIn)
    vbMatchesInliers[i]=true;
else
    vbMatchesInliers[i]=false;    // 大于阈值，则为外点，置为 false

（2）CheckFundamental()

对于函数 CheckFundamental()：理想情况下，有 ${\mathbf{p}}_2^T\mathbf{F}{\mathbf{p}}_1=0$，但由于误差存在，左式并不会恒等于零，于是，我们将它的值作为误差。

// Reprojection error in second image
//                        |f11 f12 f13|
// |a1 b1 c1| = |u2 v2 1| |f21 f22 f23|
//                        |f31 f32 f33|

const float a1 = f11*u2+f21*v2+f31;     // 先展开前两项
const float b1 = f12*u2+f22*v2+f32;
const float c1 = f13*u2+f23*v2+f33;


//          |v1|
//|a1 b1 c1||u1|=0?            // 由于误差存在，并不为零，将其作为误差值
//          |1 |
const float num1 = a1*u1+b1*v1+c1;

const float squareDist2 = num1*num1/(a1*a1+b1*b1);  // 平方误差

const float chiSquare2 = squareDist2*invSigmaSquare;

if(chiSquare2>th)
    bIn = false;
else
    score += thScore - chiSquare2;

if(bIn)
    vbMatchesInliers[i]=true;
else
    vbMatchesInliers[i]=false;

6.3.7 归一化：Normalize()

用均值和一阶距绝对值将关键点归一化，归一化可以使特征点分布均匀，增强计算稳定性。

均值

$$\bar{u}=(\sum _{i=1}^N{u}_i)/N$$
一阶距绝对值

$$|\bar{u}|=\sum _{i=0}^N\left|u_i-\bar{u}\right|/N$$

归一化坐标

$$u_i^{\prime }=\frac{u_i-\bar{u}}{|\bar{u}|}$$

令 $sX=\frac{1}{|{\bar{u}}_x|}$，$sY=\frac{1}{|{\bar{u}}_y|}$，那么变换到归一化坐标的变换矩阵为

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}sX& 0& -\text{ mean }X\ast sX\\ 0& sY& -\text{ mean }Y\ast sY\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\\ 1\end{array}\right]$$

代码

/*
 * @param vKeys             特征点在图像上的坐标
 * @param vNormalizedPoints 特征点归一化后的坐标
 * @param T                 将特征点归一化的矩阵
 */
void Initializer::Normalize(const vector<cv::KeyPoint> &vKeys, vector<cv::Point2f> &vNormalizedPoints, cv::Mat &T)
{
    float meanX = 0;
    float meanY = 0;
    const int N = vKeys.size();

    vNormalizedPoints.resize(N);

    for(int i=0; i<N; i++)
    {
        meanX += vKeys[i].pt.x;
        meanY += vKeys[i].pt.y;
    }

    meanX = meanX/N;
    meanY = meanY/N;    // 均值

    float meanDevX = 0;
    float meanDevY = 0;

    // 将所有vKeys点减去中心坐标，使x坐标和y坐标均值分别为0
    for(int i=0; i<N; i++)
    {
        vNormalizedPoints[i].x = vKeys[i].pt.x - meanX;
        vNormalizedPoints[i].y = vKeys[i].pt.y - meanY;

        meanDevX += fabs(vNormalizedPoints[i].x);
        meanDevY += fabs(vNormalizedPoints[i].y);
    }

    meanDevX = meanDevX/N;
    meanDevY = meanDevY/N;  // 一阶距绝对值

    float sX = 1.0/meanDevX;
    float sY = 1.0/meanDevY;

    // 将x坐标和y坐标分别进行尺度缩放，使得x坐标和y坐标的一阶绝对矩分别为1
    for(int i=0; i<N; i++)   // 得到归一化坐标
    {
        vNormalizedPoints[i].x = vNormalizedPoints[i].x * sX;
        vNormalizedPoints[i].y = vNormalizedPoints[i].y * sY;
    }    

    // 得到归一化坐标的变换矩阵
    // |sX  0  -meanx*sX|
    // |0   sY -meany*sY|
    // |0   0      1    |
    T = cv::Mat::eye(3,3,CV_32F);
    T.at<float>(0,0) = sX;
    T.at<float>(1,1) = sY;
    T.at<float>(0,2) = -meanX*sX;
    T.at<float>(1,2) = -meanY*sY;
}

6.3.8 检验 $\mathbf{F}$ 和 $\mathbf{H}$ 分解结果 ：CheckRT()

使用基础矩阵 $\mathbf{F}$ 分解$\mathbf{R}$、$\mathbf{t}$，数学上会得到四个可能的解,因此分解后调用函数 Initializer::CheckRT() 检验分解结果，取相机前方成功三角化数目最多的一组解。

显然只有在第一种解中，点 $\mathbf{P}$ 在两个相机中均有正深度。

同样地，单应矩阵也需要检验，从而得出符合条件的 $\mathbf{R}，\mathbf{t}$。

步骤：
① 遍历各匹配点对，调用三角化函数恢复三维点坐标
② 三维点坐标各值都必须为有限实数；
③ 深度值必须为正；
④ 三维点和两帧图像光心夹角需满足一定条件，夹角越大，视差越大，误差越小，三角化结果越准确；
⑤ 三维点的重投影误差需小于设定阈值。

将每种情况下满足要求的三维点的数目记录下来，进一步进行比较，得出最优解：
① 最优解成功三角化的数目明显优于次优解的点数目；
② 最优解的视差大于设定点阈值；
③ 最优解成功三角化的点数目大于设定阈值；
④ 最优解成功三角化点数目占所有特征点数目的 90% 以上。

6.4 三角化

三角测量恢复深度，进而求出三维点坐标。