1 Dealnnoy Number 德兰诺依数，德兰诺伊数

德兰诺依数是以法国军官、业余数学家亨利·德兰诺依（Henry Dealnnoy）的名字命名。

Henry Dealnnoy

在组合数学中，德兰诺依数描述了从(0,0)到(m,n)的格路问题中，
只允许按照(0,1）、(1,0)或者(1,1)的方式来走，一共有多少不同的方案数。

Dealnnoy Number的计算公式：

 计算结果：

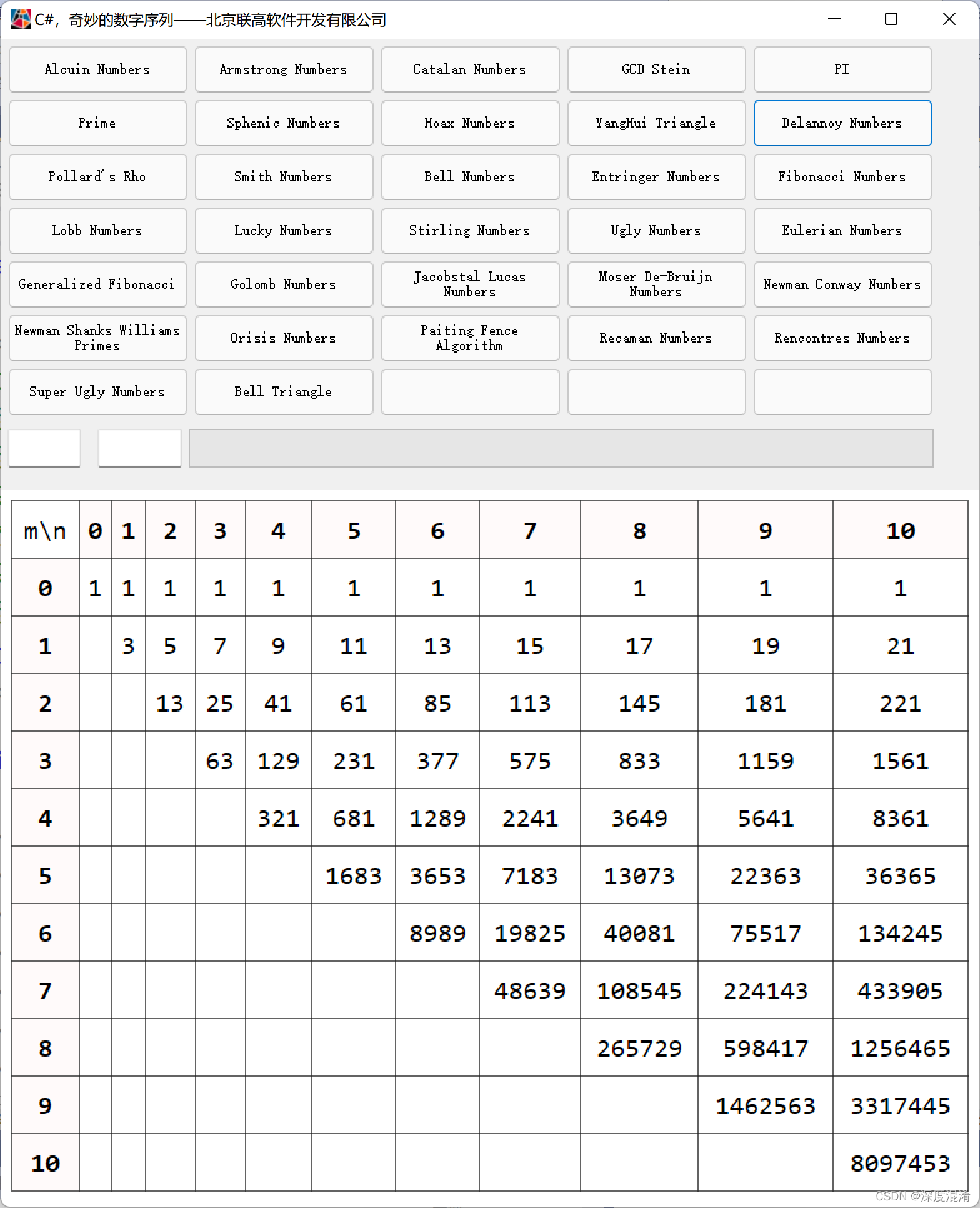
 源程序：

2 文本格式

using System;

namespace Legalsoft.Truffer.Algorithm
{
    /// <summary>
    /// Dealnnoy Number
    /// 德兰诺依数，德兰诺伊数
    /// </summary>
    public static partial class Number_Sequence
    {
        /// <summary>
        /// 德兰诺伊数（Dealnnoy Number）的原始（递归）算法
        /// n >= m
        /// </summary>
        /// <param name="n"></param>
        /// <param name="m"></param>
        /// <returns></returns>
        public static int Dealnnoy_Number(int n, int m)
        {
            if (m == 0 || n == 0)
            {
                return 1;
            }
            return Dealnnoy_Number(m - 1, n - 1) +
                   Dealnnoy_Number(m - 1, n) +
                   Dealnnoy_Number(m, n - 1);
        }

        /// <summary>
        /// 德兰诺伊数（Dealnnoy Number）的改良（非递归）算法
        /// </summary>
        /// <param name="n"></param>
        /// <param name="m"></param>
        /// <returns></returns>
        public static int Dealnnoy_Number_Second(int n, int m)
        {
            int[,] dp = new int[m + 1, n + 1];
            // 原文错误！
            for (int i = 0; i <= m; i++)
            {
                dp[i, 0] = 1;
            }
            for (int i = 0; i <= n; i++)
            {
                dp[0, i] = 1;
            }
            for (int i = 1; i <= m; i++)
            {
                for (int j = 1; j <= n; j++)
                {
                    dp[i, j] = dp[i - 1, j] + dp[i - 1, j - 1] + dp[i, j - 1];
                }
            }
            return dp[m, n];
        }
    }
}

————————————————————

POWER BY TRUFFER.CN

3 代码格式

using System;

namespace Legalsoft.Truffer.Algorithm
{
    /// <summary>
    /// Dealnnoy Number
    /// 德兰诺依数，德兰诺伊数
    /// </summary>
    public static partial class Number_Sequence
    {
        /// <summary>
        /// 德兰诺伊数（Dealnnoy Number）的原始（递归）算法
        /// n >= m
        /// </summary>
        /// <param name="n"></param>
        /// <param name="m"></param>
        /// <returns></returns>
        public static int Dealnnoy_Number(int n, int m)
        {
            if (m == 0 || n == 0)
            {
                return 1;
            }
            return Dealnnoy_Number(m - 1, n - 1) +
                   Dealnnoy_Number(m - 1, n) +
                   Dealnnoy_Number(m, n - 1);
        }

        /// <summary>
        /// 德兰诺伊数（Dealnnoy Number）的改良（非递归）算法
        /// </summary>
        /// <param name="n"></param>
        /// <param name="m"></param>
        /// <returns></returns>
        public static int Dealnnoy_Number_Second(int n, int m)
        {
            int[,] dp = new int[m + 1, n + 1];
            // 原文错误！
            for (int i = 0; i <= m; i++)
            {
                dp[i, 0] = 1;
            }
            for (int i = 0; i <= n; i++)
            {
                dp[0, i] = 1;
            }
            for (int i = 1; i <= m; i++)
            {
                for (int j = 1; j <= n; j++)
                {
                    dp[i, j] = dp[i - 1, j] + dp[i - 1, j - 1] + dp[i, j - 1];
                }
            }
            return dp[m, n];
        }
    }
}