深度强化学习(DRL)
本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。
参考链接
Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL
源代码链接:https://github.com/DeepRLChinese/DeepRL-Chinese
B站视频:【王树森】深度强化学习(DRL)
豆瓣: 深度强化学习
文章目录
- 深度强化学习(DRL)
- 策略学习高级技巧
- Trust Region Policy Optimization (TRPO)
- 置信域方法
- 策略学习
- TRPO 数学推导
- 训练流程
- 后记
策略学习的高级技巧:置信域策略优化 (TRPO)
PPO算法就是在TRPO的基础上推出的。
策略学习高级技巧
本章介绍策略学习的高级技巧。介绍置信域策略优化 (TRPO), 它是一种策略学习方法,可以代替策略梯度方法。
Trust Region Policy Optimization (TRPO)
置信域策略优化 (trust region policy optimization, TRPO) 是一种策略学习方法,跟以前学的策略梯度有很多相似之处。跟策略梯度方法相比,TRPO 有两个优势:第一,TRPO 表现更稳定,收敛曲线不会剧烈波动,而且对学习率不敏感;第二,TRPO 用更少的经验(即智能体收集到的状态、动作、奖励) 就能达到与策略梯度方法相同的表现。
学习TRPO 的关键在于理解置信域方法(trustregion methods)。置信域方法不是TRPO 的论文提出的,而是数值最优化领域中一类经典的算法,历史至少可以追溯到 1970 年。TRPO 论文的贡献在于巧妙地把置信域方法应用到强化学习中,取得非常好的效果。
置信域方法
有这样一个优化问题: max θ J ( θ ) \max_{\boldsymbol{\theta}}J(\boldsymbol{\theta}) maxθJ(θ)。这里的 J ( θ ) J(\boldsymbol{\theta}) J(θ) 是目标函数, θ \theta θ 是优化变量。求解这个优化问题的目的是找到一个变量 θ \theta θ 使得目标函数 J ( θ ) J(\theta) J(θ) 取得最大值。有各种各样的优化算法用于解决这个问题。几乎所有的数值优化算法都是做这样的迭代:
θ n e w ← U p d a t e ( Data; θ n o w ) . \begin{array}{rcl}\theta_\mathrm{new}&\leftarrow&\mathrm{Update}\left(\text{Data; }\theta_\mathrm{now}\right).\end{array} θnew←Update(Data; θnow).
此处的 θ n o w \theta_\mathrm{now} θnow 和 θ n e w \theta_\mathrm{new} θnew 分别是优化变量当前的值和新的值。不同算法的区别在于具体怎么样利用数据更新优化变量。
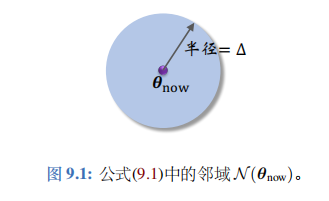
置信域方法用到一个概念——置信域。下面介绍置信域。给定变量当前的值 θ n o w \theta_\mathrm{now} θnow,用 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 表示 θ n o w \theta_\mathrm{now} θnow 的一个邻域。举个例子:
N
(
θ
n
o
w
)
=
{
θ
∣
∥
θ
−
θ
n
o
w
∥
2
≤
Δ
}
.
(
9.1
)
\mathcal{N}(\theta_{\mathrm{now}})\:=\:\Big\{\theta\:\Big|\:\left\|\theta-\theta_{\mathrm{now}}\right\|_{2}\leq\Delta\Big\}.\quad(9.1)
N(θnow)={θ
∥θ−θnow∥2≤Δ}.(9.1)
这个例子中,集合
N
(
θ
n
o
w
)
\mathcal{N} ( \theta_\mathrm{now})
N(θnow) 是以
θ
n
o
w
\theta_\mathrm{now}
θnow 为球心、 以
Δ
\Delta
Δ为半径的球;见右图。球中的点都足够接近
θ
n
o
w
\theta_\mathrm{now}
θnow。
置信域方法需要构造一个函数 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow),这个函数要满足这个条件:
L ( θ ∣ θ n o w ) 很接近 J ( θ ) , ∀ θ ∈ N ( θ n o w ) , L(\boldsymbol{\theta}\mid\boldsymbol{\theta_\mathrm{now}})\text{ 很接近 }J(\boldsymbol{\theta}),\quad\forall\boldsymbol{\theta}\in\mathcal{N}(\boldsymbol{\theta_\mathrm{now}}), L(θ∣θnow) 很接近 J(θ),∀θ∈N(θnow),
那么集合 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow)就被称作置信域。顾名思义,在 θ n o w \theta_\mathrm{now} θnow的邻域上,我们可以信任 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow), 可以拿 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 来替代目标函数 J ( θ ) J(\theta) J(θ) 。
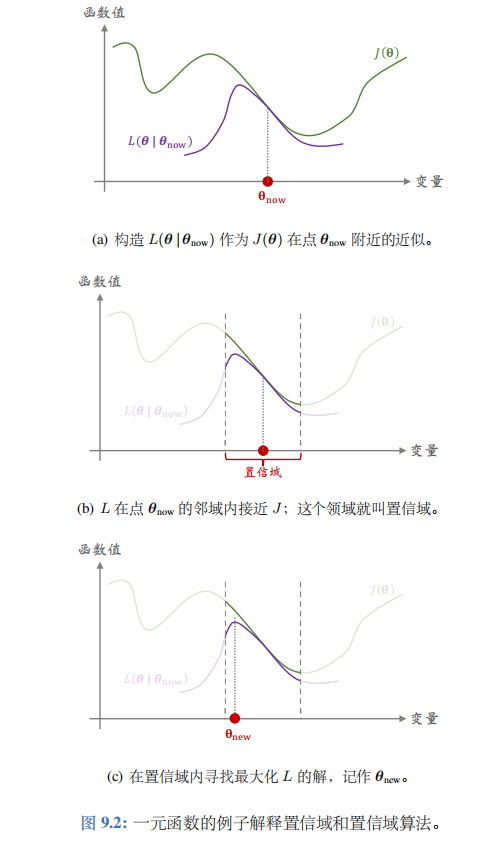
图 9.2 用一个一元函数的例子解释 J ( θ ) J(\theta) J(θ) 和 L ( θ ∣ θ n o w ) L(\theta\mid\theta_\mathrm{now}) L(θ∣θnow) 的关系。图中横轴是优化变量 θ \theta θ,纵轴是函数值。如图 9.2(a)所示,函数 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 未必在整个定义域上都接近 J ( θ ) J(\theta) J(θ),而只是在 θ n o w \theta_\mathrm{now} θnow的领域里接近 J ( θ ) J(\theta) J(θ)。 θ n o w \theta_\mathrm{now} θnow 的邻域就叫做置信域。
通常来说, J J J是个很复杂的函数,我们甚至可能不知道 J J J 的解析表达式(比如 J J J 是某个函数的期望)。而我们人为构造出的函数 L L L 相对较为简单,比如 L L L 是 J J J 的蒙特卡洛近似,或者是 J J J在 θ n o w \theta_\mathrm{now} θnow这个点的二阶泰勒展开。既然可以信任 L L L,那么不妨用 L L L 代替复杂的函数 J J J,然后对 L L L做最大化。这样比直接优化 J J J 要容易得多。这就是置信域方法的思想。
具体来说,置信域方法做下面这两个步骤,一直重复下去,当无法让 J J J 的值增大的时候终止算法。
第一步——做近似:给定 θ n o w \theta_\mathrm{now} θnow,构造函数 L ( θ ∣ θ n ε w ) L(\theta\mid\theta_{n\varepsilon w}) L(θ∣θnεw),使得对于所有的 θ ∈ N ( θ n o w ) \theta\in \mathcal{N} ( \theta_\mathrm{now}) θ∈N(θnow),函数值 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 与 J ( θ ) J(\theta) J(θ) 足够接近。图9.2(b) 解释了做近似这一步。
第二步一一最大化:在置信域 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 中寻找变量 θ \theta θ 的值, 使得函数 L L L 的值最大化。把找到的值记作
θ n e w = a r g m a x θ ∈ N ( θ n o w ) L ( θ ∣ θ n o w ) . \theta_{\mathrm{new}}\:=\:\underset{\theta\in\mathcal{N}(\theta_{\mathrm{now}})}{\operatorname*{\mathrm{argmax}}}\:L(\boldsymbol{\theta}\mid\boldsymbol{\theta_{\mathrm{now}}})\:. θnew=θ∈N(θnow)argmaxL(θ∣θnow).
图 9.2( c) 解释了最大化这一步。
置信域方法其实是一类算法框架,而非一个具体的算法。有很多种方式实现实现置信域方法。第一步需要做近似,而做近似的方法有多种多样,比如蒙特卡洛、二阶泰勒展开。第二步需要解一个带约束的最大化问题;求解这个问题又需要单独的数值优化算法,比如梯度投影算法、拉格朗日法。除此之外,置信域 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 也有多种多样的选择, 既可以是球,也可以是两个概率分布的 KL 散度 (KL Divergence)。
ChatGPT对梯度投影算法的介绍
梯度投影算法的基本步骤可以通过数学公式进行介绍。考虑带有约束的优化问题:
m i n x f ( x ) min_{x} f(x) minxf(x)
其中 (f(x)) 是目标函数,(x) 是优化变量,同时满足一组约束条件:
g i ( x ) ≤ 0 , i = 1 , 2 , … , m g_i(x) \leq 0, \quad i = 1, 2, \ldots, m gi(x)≤0,i=1,2,…,m
梯度投影算法的迭代过程如下:
-
初始化: 选择初始解 ( x 0 x_0 x0),设置学习率 ( α \alpha α) 和停止准则。
-
梯度计算: 计算目标函数在当前解 ( x k x_k xk) 处的梯度 ( ∇ f ( x k ) \nabla f(x_k) ∇f(xk))。
-
梯度投影: 将梯度投影到满足约束条件的空间中。假设投影操作为 (P(x)),则更新方向为 ( Δ x k = P ( x k − α ∇ f ( x k ) ) − x k \Delta x_k = P(x_k - \alpha \nabla f(x_k)) - x_k Δxk=P(xk−α∇f(xk))−xk)。
-
更新变量: 使用投影后的梯度信息来更新变量 ( x k x_k xk):
x k + 1 = x k + α Δ x k x_{k+1} = x_k + \alpha \Delta x_k xk+1=xk+αΔxk
- 收敛判断: 判断算法是否达到停止条件,例如目标函数的变化足够小或者达到预定的迭代次数。
在这里,梯度投影的关键在于投影操作 (P(x)) 的定义。具体的投影形式取决于约束条件的性质。例如,对于线性约束 ( g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0),投影操作可以表示为 ( P ( x ) = max ( 0 , g i ( x ) ) P(x) = \max(0, g_i(x)) P(x)=max(0,gi(x)))。对于更一般的非线性约束,可能需要使用专门的数学工具或算法来进行梯度投影。
需要注意的是,实际应用中可能需要根据具体问题对算法进行调整和定制。
策略学习
首先复习策略学习的基础知识。策略网络记作 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ), 它是个概率质量函数。动作价值函数记作 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a),它是回报的期望。状态价值函数记作
V π ( s ) = E A ∼ π ( ⋅ ∣ s ; θ ) [ Q π ( s , A ) ] = ∑ a ∈ A π ( a ∣ s ; θ ) ⋅ Q π ( s , a ) . ( 9.2 ) V_{\pi}(s)\:=\:\mathbb{E}_{A\sim\pi(\cdot|s;\theta)}\big[Q_{\pi}(s,A)\big]\:=\:\sum_{a\in\mathcal{A}}\pi(a|s;\boldsymbol{\theta})\cdot Q_{\pi}(s,a). \quad(9.2) Vπ(s)=EA∼π(⋅∣s;θ)[Qπ(s,A)]=a∈A∑π(a∣s;θ)⋅Qπ(s,a).(9.2)
注意, V π ( s ) V_{\pi}(s) Vπ(s) 依赖于策略网络 π, 所以依赖于 π \pi π 的参数 θ \theta θ。策略学习的目标函数是
J ( θ ) = E S [ V π ( S ) ] . ( 9.3 ) J(\boldsymbol{\theta})=\mathbb{E}_{S}\big[V_{\pi}(S)\big].\quad(9.3) J(θ)=ES[Vπ(S)].(9.3)
J ( θ ) J(\theta) J(θ) 只依赖于 θ \theta θ,不依赖于状态 S S S 和动作 A A A。前面介绍的策略梯度方法 (包括 REINFORCE 和 Actor-Critic) 用蒙特卡洛近似梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ), 得到随机梯度,然后做随机梯度上升更新 θ \theta θ,使得目标函数 J ( θ ) J(\theta) J(θ) 增大。
下面我们要把目标函数 J ( θ ) J(\boldsymbol{\theta}) J(θ) 变换成一种等价形式。从等式(9.2)出发,把状态价值写成
V
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
;
θ
n
o
w
)
⋅
π
(
a
∣
s
;
θ
)
π
(
a
∣
s
;
θ
n
o
w
)
⋅
Q
π
(
s
,
a
)
=
E
A
∼
π
(
⋅
∣
s
;
θ
n
o
w
)
[
π
(
A
∣
s
;
θ
)
π
(
A
∣
s
;
θ
n
o
w
)
⋅
Q
π
(
s
,
A
)
]
.
(
9.4
)
\begin{gathered} V_{\pi}(s) =\:\sum_{a\in\mathcal{A}}\pi\big(a\big|\:s;\:\theta_{\mathrm{now}}\big)\:\cdot\:\frac{\pi(a\:|\:s;\:\boldsymbol{\theta})}{\pi(a\:|s;\:\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:Q_{\pi}(s,a) \\ =\quad\mathbb{E}_{A\sim\pi(\cdot|s;\theta_{\mathrm{now}})}\bigg[\:\frac{\pi(A\:|\:s;\:\boldsymbol{\theta})}{\pi(A\:|\:s;\:\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:Q_{\pi}(s,A)\:\bigg]. \end{gathered}\quad(9.4)
Vπ(s)=a∈A∑π(a
s;θnow)⋅π(a∣s;θnow)π(a∣s;θ)⋅Qπ(s,a)=EA∼π(⋅∣s;θnow)[π(A∣s;θnow)π(A∣s;θ)⋅Qπ(s,A)].(9.4)
第一个等式很显然,因为连加中的第一项可以消掉第二项的分母。第二个等式把策略网络
π
(
A
∣
s
;
θ
n
o
w
)
\pi(A|s;\boldsymbol{\theta}_\mathrm{now})
π(A∣s;θnow) 看做动作
A
A
A 的概率质量函数,所以可以把连加写成期望。由公式 (9.3) 与(9.4) 可得定理 9.1。定理 9.1 是 TRPO 的关键所在,甚至可以说 TRPO 就是从这个公式推出的。

定理 9.1. 目标函数的等价形式目标函数 J ( θ ) J(\theta) J(θ)可以等价写成:
J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S , θ n o w ) [ π ( A ∣ S ; θ ) π ( A ∣ S ; θ n o w ) ⋅ Q π ( S , A ) ] ] . J(\boldsymbol{\theta})\:=\:\mathbb{E}_{S}\bigg[\mathbb{E}_{A\sim\pi(\cdot|S,\boldsymbol{\theta}_{\mathrm{now}})}\bigg[\frac{\pi(A\:|\:S;\:\boldsymbol{\theta})}{\pi(A\:|\:S;\:\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:Q_{\pi}(S,A)\bigg]\bigg]. J(θ)=ES[EA∼π(⋅∣S,θnow)[π(A∣S;θnow)π(A∣S;θ)⋅Qπ(S,A)]].
上面 Q π Q_\pi Qπ 中的 π \pi π 指的是 π ( A ∣ S ; θ ) \pi(A|S;\boldsymbol{\theta}) π(A∣S;θ)。
公式中的期望是关于状态 S S S 和动作 A A A 求的。状态 S S S 的概率密度函数只有环境知道, 而我们并不知道,但是我们可以从环境中获取 S S S 的观测值。动作 A A A 的概率质量函数是策略网络 π ( A ∣ S ; θ n o w ) \pi(A|S;\theta_\mathrm{now}) π(A∣S;θnow); 注意,策略网络的参数是旧的值 θ n o w \theta_\mathrm{now} θnow.
TRPO 数学推导
前面介绍了数值优化的基础和价值学习的基础,终于可以开始推导 TRPO。TRPO 是置信域方法在策略学习中的应用,所以 TRPO 也遵循置信域方法的框架,重复做近似和最大化这两个步骤,直到算法收敛。收敛指的是无法增大目标函数 J ( θ ) J(\theta) J(θ) , 即无法增大期望回报。
第一步——做近似:
我们从定理 9.1 出发。定理把目标函数 J ( θ ) J(\theta) J(θ) 写成了期望的形式。我们无法直接算出期望,无法得到 J ( θ ) J(\theta) J(θ) 的解析表达式;原因在于只有环境知道状态 S S S 的概率密度函数,而我们不知道。我们可以对期望做蒙特卡洛近似,从而把函数 J J J 近似成函数 L L L。用策略网络 π ( A ∣ S ; θ n o w ) \pi(A|S;\theta_\mathrm{now}) π(A∣S;θnow) 控制智能体跟环境交互,从头到尾玩完一局游戏观测到一条轨迹:
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , ⋯ , s n , a n , r n . s_1,\:a_1,\:r_1,\:s_2,\:a_2,\:r_2,\:\cdots,\:s_n,\:a_n,\:r_n. s1,a1,r1,s2,a2,r2,⋯,sn,an,rn.
其中的状态 { s t } t = 1 n \{s_t\}_{t=1}^n {st}t=1n 都是从环境中观测到的,其中的动作 { a t } t = 1 n \{a_t\}_{t=1}^n {at}t=1n 都是根据策略网络 π ( ⋅ ∣ s t ; θ n o w ) \pi(\cdot|s_t;\theta_\mathrm{now}) π(⋅∣st;θnow) 抽取的样本。所以,
π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ n o w ) ⋅ Q π ( s t , a t ) ( 9.5 ) \frac{\pi(a_t\mid s_t;\boldsymbol{\theta})}{\pi(a_t\mid s_t;\boldsymbol{\theta_\mathrm{now}})}\cdot Q_\pi(s_t,a_t) \quad(9.5) π(at∣st;θnow)π(at∣st;θ)⋅Qπ(st,at)(9.5)
是对定理 9.1 中期望的无偏估计。我们观测到了 n n n 组状态和动作,于是应该对公式 (9.5) 求平均,把得到均值记作:
L ( θ ∣ θ n o w ) = 1 n ∑ t = 1 n π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ n o w ) ⋅ Q π ( s t , a t ) ⏟ 定理 9.1 中期望的无偏估计 . ( 9.6 ) L(\boldsymbol{\theta}\:|\:\boldsymbol{\theta_\mathrm{now}})\:=\:\frac{1}{n}\sum_{t=1}^{n}\underbrace{\frac{\pi(a_{t}\:|\:s_{t};\boldsymbol{\theta})}{\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta_\mathrm{now}}\:)}\:\cdot\:Q_{\pi}\left(s_{t},a_{t}\right)}_{定理 9.1 中期望的无偏估计}\:.\quad(9.6) L(θ∣θnow)=n1t=1∑n定理9.1中期望的无偏估计 π(at∣st;θnow)π(at∣st;θ)⋅Qπ(st,at).(9.6)
既然连加里每一项都是期望的无偏估计,那么 n n n 项的均值 L L L 也是无偏估计。所以可以拿 L L L作为目标函数 J J J 的蒙特卡洛近似。
公式(9.6) 中的 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 是对目标函数 J ( θ ) J(\theta) J(θ) 的近似。可惜我们还无法直接对 L L L 求最大化,原因是我们不知道动作价值 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)。解决方法是做两次近似:
Q π ( s t , a t ) ⟹ Q π o l d ( s t , a t ) ⟹ u t . Q_{\pi}(s_{t},a_{t})\quad\Longrightarrow\quad Q_{\pi_{\mathrm{old}}}(s_{t},a_{t})\quad\Longrightarrow\quad u_{t}. Qπ(st,at)⟹Qπold(st,at)⟹ut.
公式中 Q π Q_\pi Qπ 中的策略是 π ( a t ∣ s t ; θ ) \pi(a_t\mid s_t;\boldsymbol{\theta}) π(at∣st;θ), 而 Q π o l d Q_\mathrm{\pi_\mathrm{old}} Qπold 中的策略则是旧策略 π ( a t ∣ s t ; θ n o w ) \pi(a_t\mid s_t;\boldsymbol{\theta_\mathrm{now}}) π(at∣st;θnow)。我们用旧策略 π ( a t ∣ s t ; θ n o w ) \pi(a_t\mid s_t;\theta_\mathrm{now}) π(at∣st;θnow)生成轨迹 { ( s j , a j , r j , s j + 1 ) } j = 1 n \{(s_j,a_j,r_j,s_{j+1})\}_{j=1}^n {(sj,aj,rj,sj+1)}j=1n。所以折扣回报
u t = r t + γ ⋅ r t + 1 + γ 2 ⋅ r t + 2 + ⋯ + γ n − t ⋅ r n u_{t}\:=\:r_{t}+\gamma\cdot r_{t+1}+\gamma^{2}\cdot r_{t+2}+\cdots+\gamma^{n-t}\cdot r_{n} ut=rt+γ⋅rt+1+γ2⋅rt+2+⋯+γn−t⋅rn
是对 Q π o l d Q_\mathrm{\pi_\mathrm{old}} Qπold 的近似,而未必是对 Q π Q_\mathrm{\pi} Qπ 的近似。仅当 θ \theta θ接近 θ r o w \theta_\mathrm{row} θrow 的时候, u t u_t ut 才是 Q π Q_\pi Qπ 的有效近似。这就是为什么要强调置信域,即 θ \theta θ在 θ n o w \theta_\mathrm{now} θnow的邻域中。
拿 u t u_t ut 替代 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at),那么公式(9.6) 中的 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 变成了
L ~ ( θ ∣ θ n o w ) = 1 n ∑ t = 1 n π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ n o w ) ⋅ u t . ( 9.7 ) \boxed{\quad\tilde{L}(\boldsymbol{\theta}\mid\boldsymbol{\theta}_{\mathrm{now}})=\frac1n\sum_{t=1}^n\frac{\pi(a_t\mid s_t;\boldsymbol{\theta})}{\pi(a_t\mid s_t;\boldsymbol{\theta}_{\mathrm{now}})}\cdot u_t.}\quad(9.7) L~(θ∣θnow)=n1t=1∑nπ(at∣st;θnow)π(at∣st;θ)⋅ut.(9.7)
总结一下,我们把目标函数 J J J 近似成 L L L,然后又把 L L L 近似成 L ~ \tilde{L} L~。在第二步近似中,我们需要假设 θ \theta θ 接近 θ n o w \theta_\mathrm{now} θnow。
第二步——最大化:
TRPO 把公式 (9.7) 中的 L ~ ( θ ∣ θ n o w ) \tilde{L}(\theta|\theta_\mathrm{now}) L~(θ∣θnow) 作为对目标函数 J ( θ ) J(\theta) J(θ) 的近似,然后求解这个带约束的最大化问题:
max θ L ~ ( θ ∣ θ n o w ) ; s . t . θ ∈ N ( θ n o w ) . ( 9.8 ) \boxed{\max_{\theta}\tilde{L}\left(\boldsymbol{\theta}\mid\boldsymbol{\theta}_{\mathrm{now}}\right);\quad\mathrm{s.t.~}\boldsymbol{\theta}\in\mathcal{N}(\boldsymbol{\theta}_{\mathrm{now}}).}\quad(9.8) θmaxL~(θ∣θnow);s.t. θ∈N(θnow).(9.8)
公式中的 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 是置信域,即 θ n o w \theta_\mathrm{now} θnow的一个邻域。该用什么样的置信域呢?
- 一种方法是用以 θ n o w \theta_\mathrm{now} θnow为球心、以 Δ \Delta Δ为半径的球作为置信域。这样的话,公式(9.8)就变成
max θ L ~ ( θ ∣ θ n o w ) ; s.t. ∥ θ − θ n o w ∥ 2 ≤ Δ . ( 9.9 ) \max_{\boldsymbol{\theta}}\:\tilde{L}(\boldsymbol{\theta}\:|\:\boldsymbol{\theta}_{\mathrm{now}});\quad\text{s.t.}\:\left\|\boldsymbol{\theta}-\boldsymbol{\theta}_{\mathrm{now}}\right\|_2\leq\Delta.\quad(9.9) θmaxL~(θ∣θnow);s.t.∥θ−θnow∥2≤Δ.(9.9)
- 另一种方法是用 KL 散度衡量两个概率质量函数—— π ( ⋅ ∣ s i ; θ n o w ) \pi(\cdot|s_i;\theta_\mathrm{now}) π(⋅∣si;θnow) 和 π ( ⋅ ∣ s i ; θ ) \pi(\cdot|s_i;\theta) π(⋅∣si;θ)—— 的距离。两个概率质量函数区别越大,它们的 KL 散度就越大。反之,如果 θ \theta θ 很接近 θ n o w \theta_\mathrm{now} θnow,那么两个概率质量函数就越接近。用 KL 散度的话,公式(9.8)就变成
max θ L ~ ( θ ∣ θ n o w ) ; s . t . 1 t ∑ i = 1 t KL [ π ( ⋅ ∣ s i ; θ n o w ) ∥ π ( ⋅ ∣ s i ; θ ) ] ≤ Δ . ( 9.10 ) \max_{\boldsymbol{\theta}}\tilde{L}\left(\boldsymbol{\theta}\mid\boldsymbol{\theta}_{\mathrm{now}}\right);\quad\mathrm{s.t.}\:\frac{1}{t}\sum_{i=1}^{t}\:\text{KL}\Big[\:\pi\big(\:\cdot\:\big|\:s_{i};\:\boldsymbol{\theta}_{\mathrm{now}}\big)\:\big\Vert\:\pi\big(\:\cdot\:\big|\:s_{i};\:\boldsymbol{\theta}\big)\:\Big]\:\le\:\Delta. \quad(9.10) θmaxL~(θ∣θnow);s.t.t1i=1∑tKL[π(⋅ si;θnow) π(⋅ si;θ)]≤Δ.(9.10)
用球作为置信域的好处是置信域是简单的形状,求解最大化问题比较容易,但是用球做置信域的实际效果不如用 KL 散度。
TRPO 的第二步—最大化——需要求解带约束的最大化问题(9.9) 或者 (9.10)。注意,这种问题的求解并不容易;简单的梯度上升算法并不能解带约束的最大化问题。数值优化教材通常有介绍带约束问题的求解,有兴趣的话自己去阅读数值优化教材,这里就不详细解释如何求解问题 (9.9) 或者 (9.10)。读者可以这样看待优化问题:只要你能把一个优化问题的目标函数和约束条件解析地写出来,通常会有数值算法能解决这个问题。
训练流程
在本节的最后,我们总结一下用 TRPO 训练策略网络的流程。TRPO 需要重复做近似和最大化这两个步骤:
- 做近似——构造函数 L ~ \tilde{L} L~ 近似目标函数 J ( θ ) : J(\theta): J(θ):
(a). 设当前策略网络参数是 θ n o w \theta_\mathrm{now} θnow。用策略网络 π ( a ∣ s ; θ n o w ) \pi(a\mid s;\theta_\mathrm{now}) π(a∣s;θnow) 控制智能体与环境交互,玩完一局游戏,记录下轨迹:
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , ⋯ , s n , a n , r n . s_{1},\:a_{1},\:r_{1},\:s_{2},\:a_{2},\:r_{2},\:\cdots,\:s_{n},\:a_{n},\:r_{n}. s1,a1,r1,s2,a2,r2,⋯,sn,an,rn.
(b). 对于所有的
t
=
1
,
⋯
,
n
t=1,\cdots,n
t=1,⋯,n, 计算折扣回报
u
t
=
∑
k
=
t
n
γ
k
−
t
⋅
r
k
u_t=\sum_{k=t}^n\gamma^{k-t}\cdot r_k
ut=∑k=tnγk−t⋅rk.
(c ). 得出近似函数:
L
~
(
θ
∣
θ
n
o
w
)
=
1
n
∑
t
=
1
n
π
(
a
t
∣
s
t
;
θ
)
π
(
a
t
∣
s
t
;
θ
n
o
w
)
⋅
u
t
.
\tilde{L}\left(\boldsymbol{\theta}\:|\:\boldsymbol{\theta}_{\mathrm{now}}\right)\:=\:\frac{1}{n}\sum_{t=1}^{n}\frac{\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta})}{\pi(a_{t}\:|\:s_{t};\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:u_{t}.
L~(θ∣θnow)=n1t=1∑nπ(at∣st;θnow)π(at∣st;θ)⋅ut.
- 最大化——用某种数值算法求解带约束的最大化问题:
θ n e w = a r g m a x L ~ ( θ ∣ θ n o w ) ; s . t . ∥ θ − θ n o w ∥ 2 ≤ Δ . \theta_{\mathrm{new}}\:=\:\mathrm{argmax}\:\tilde{L}(\boldsymbol{\theta}\:|\:\theta_{\mathrm{now}});\quad\mathrm{s.t.}\:\left\|\theta-\theta_{\mathrm{now}}\right\|_{2}\:\leq\:\Delta. θnew=argmaxL~(θ∣θnow);s.t.∥θ−θnow∥2≤Δ.
此处的约束条件是二范数距离。可以把它替换成 KL 散度,即公式 (9.10)。
TRPO 中有两个需要调的超参数:一个是置信域的半径 Δ \Delta Δ, 另一个是求解最大化问题的数值算法的学习率。通常来说, Δ \Delta Δ 在算法的运行过程中要逐渐缩小。虽然 TRPO 需要调参,但是 TRPO 对超参数的设置并不敏感。即使超参数设置不够好,TRPO 的表现也不会太差。相比之下,策略梯度算法对超参数更敏感。
TRPO 算法真正实现起来并不容易,主要难点在于第二步一一最大化。不建议读者自己去实现 TRPO。
后记
截至2024年1月30日16点52分,完成王树森的深度强化学习视频课程。后面的多智能体部分听完了两节课,但是没有做相应的笔记。
回顾这几天的学习:2024年1月25日晚上闲来无事确定学习王树森的这门课,2024年1月26日正式开始学习,截至2024年1月30日,总共花费5天时间学习深度强化学习。形成了系列笔记。
后续可能会跟进动手学强化学习这门课。
2024年1月31日坐高铁回家过年,在回家之前完成了自己设定的计划——学习完王树森的《深度强化学习》。看到TODO list上又完成了一件事,整个人还是比较开心的。
2024春节快乐。



![[AG32VF407]国产MCU+FPGA Verilog编写控制2路gpio输出不同频率方波实验](https://img-blog.csdnimg.cn/direct/ad5222f141b7492fa91eabd963001865.png)

![洛谷P8599 [蓝桥杯 2013 省 B] 带分数](https://img-blog.csdnimg.cn/direct/2012e5afc8034938b4f4e014ebcd1ca8.png)