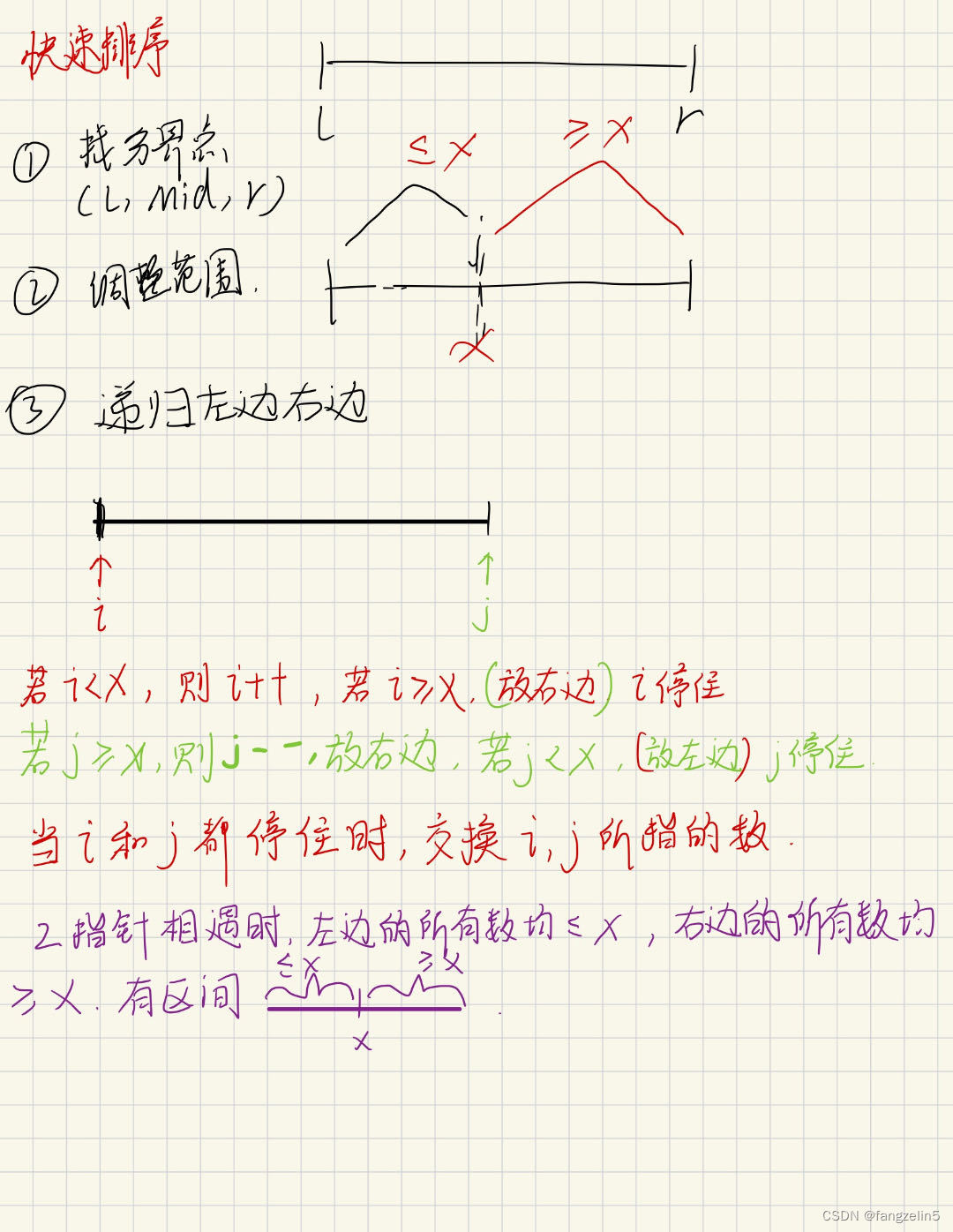
快速排序思想:
1、找一个分界点。
2、在分界点两边开始调整范围。
3、递归两边,重复。
例题:
给定你一个长度为 n的整数数列。
请你使用快速排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 n
第二行包含 n个整数(所有整数均在 1∼1e8范围内),表示整个数列。
输出格式
输出共一行,包含 n个整数,表示排好序的数列。
数据范围
1≤n≤100000
输入样例:
5 3 1 2 4 5输出样例:
1 2 3 4 5代码如下:
#include <iostream>
using namespace std;
const int N=100010;
int q[N]={0};
void quick_sort(int q[],int l,int r)
{
if(l>=r) return; //如果左边界=右边界,直接退出
int i=l-1; //让指针往外走一位,为了就是保证能够先执行++操作,使得具有一般性
int j=r+1;
int x=q[l+r>>1];
/*
位运算/2,取得对比值是中间数,如果取两边的边缘值,
可能造成超时。
*/
while(i<j)
{
do i++ ;while(q[i]<x);
do j-- ;while(q[j]>x);
if(i<j)
swap(q[i],q[j]);
}
/*
快速排序,当左边指针i一路满足条件时,不断往下走。当i遇到不满足条件的,
进行j--操作,当j不满足时,两个while都跳出去了,此时若i<j,则执行交换功能,
将二者所指向的具体数字交换,
1、如果此时仍然满足i<j,那么重复大while循环
2、如果i>j,那么直接跳出大while循环,进入下面的递归。
*/
quick_sort(q,l,j);
quick_sort(q,j+1,r);
/*
接2、此时应该是i到了j的右边,想要将区间划分,只能让左边界到靠左边的j
即sort(q,l,j);
同理,右边界的起始点是j+1,则有:
sort(q,j+1,r);
*/
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&q[i]);
quick_sort(q,0,n-1);
for(int i=0;i<n;i++)
printf("%d ",q[i]);
return 0;
}此算法的时间复杂度是
快速选择算法思想:
1、找出分界点x
2、左边的所有元素<=x,右边的所有元素>=x
3、左区间元素个数为s1,右区间为s2.如果所选择的元素位数k在左区间,则为位置为k,落在右区间,则所在位置为r-s1
4、k在左边,递归左边。k在右边,递归右边
给定一个长度为 n 的整数数列,以及一个整数 k,请用快速选择算法求出数列从小到大排序后的第 k 个数。
输入格式
第一行包含两个整数 n 和 k。
第二行包含 n 个整数(所有整数均在 1∼1e8 范围内),表示整数数列。
输出格式
输出一个整数,表示数列的第 k个数。
数据范围
1≤n≤100000
1≤k≤n输入样例:
5 3 2 4 1 5 3输出样例:
3
代码如下:
#include <iostream>
using namespace std;
int n;
int k;
const int N =1e5+10;
int q[N];
int quick_sort(int q[],int l,int r,int k)
{
if(l==r) //区间分割只剩下一个元素,此元素为所求元素
return q[l];
int x = q[l];
int i=l-1;
int j=r+1;
while(i<j)
{
while(q[++i] < x);
while(q[--j] > x);
if(i<j) swap(q[i],q[j]);
}
int s1=j+1-l; //s1是此时左边的元素个数
if(k<=s1) return quick_sort(q,l,j,k); //k在左边,递归左边即可
if(k>s1) return quick_sort(q,j+1,r,k-s1); //k在右边,递归右边即可
//注意k在左右两区间的位置不同
}
int main()
{
cin>>n>>k;
for(int i=0;i<n;i++)
cin>>q[i];
cout<<quick_sort(q,0,n-1,k);
return 0;
}此算法的时间复杂度为:
如果先用快速排序算法排序,再选出第k个数,时间复杂度相对较高。