C语言KR圣经笔记 6.4结构体指针 6.5自引用结构体

6.4 结构体指针

为了说明结构体指针和数组的某些注意事项，我们把上一节的关键字计数程序再写一次，不过这回使用指针而不是数组下标。

keytab 的外部声明不需要动，但 main 和 binsearch 确实需要修改。

#include <stdio.h>
#include <ctype.h>
#include <string.h>
#define MAXWORD 1000

int getword(char *, int);
struct key *binsearch(char *, struct key *, int);

/* C语言关键字计数，指针版本 */
main()
{
    char word[MAXWORD];
    struct key *p;

    while (getword(word, MAXRORD) != EOF)
        if (isalpha(word[0]))
            if ((p=binsearch(word, keytab, NKEYS)) != NULL)
                p->count++;
    for (p = keytab; p < keytab + NKEYS; p++)
        if (p->count > 0)
            printf("%4d %s", p->count, p->word);
    return 0;
}

/* binsearch：在tab[0]...tab[n-1]中查找word */
struct key *binsearch(char *word, struct key *tab, int n)
{
    int cond;
    struct key *low = &tab[0];
    struct key *high = &tab[n-1];
    struct key *mid;

    while (low <= high) {
        mid = low + (high - low) / 2;
        if ((cond = strcmp(word, mid->word)) < 0)
            high = mid;
        else if (cond > 0)
            low = mid + 1;
        else
            return mid;
    }
    return NULL;
}

这里有几个地方值得一提。首先，binsearch 的声明必须指出它返回 struct key 的指针而不是（第三章版本里面的）整数；在函数原型和 binsearch 内部都声明了这一点。如果 binsearch 找到一个单词，则返回其指针；若没找到，则返回NULL。

第二，keytab 的元素现在通过指针和不是数组下标来访问。这要求对 binsearch 做大改。

low 和 high 的初始化表达式现在分别是指向表的开头和结尾的指针。

中间元素的计算不能简单地使用

mid = (low + high) / 2     /* 错误 */

因为两个指针相加是非法的。然而，两个指针相减是合法的，因此 high - low 为元素的个数，而

mid = low + (high-low) / 2

就使 mid 指向 low 和 high 中间的元素。

最重要的改变在于调整算法，以保证它不会生成非法的指针，或是试图访问数组之外的元素。问题是 &tab[-1] 和 &tab[n] 都在数组 tab 的范围之外。前者是严格非法的，而后者的解引用是非法的。然而，C语言的定义保证，对于超过数组末尾后的第一个元素（即 &tab[n]），其指针运算能正确执行。

在 main 函数中，有

for (p = keytab; p < keytab + NKEYS; p++)

如果 p 是指向结构体的指针，对 p 的指针运算会将结构体的大小考虑在内，因此 p++ 能正确地对 p 递增，使其指向结构体数组的下一个元素，而 for 循环中的判断条件能在正确的时候停止循环。

但是，不能假定结构体的长度是其成员长度之和。由于不同对象的对齐要求，结构体中可能存在未名的“空洞”。例如，如果 char 是一字节而 int 是四字节，如下结构体

struct {
    char c;
    int i;
};

可能会占八个字节，而不是五个。sizeof 操作符能返回正确的值。

最后，说一些关于程序格式的题外话：当函数返回复杂类型如结构体指针时，如

struct key *binsearch(char *word, struct key *tab, int n)

此时在文本编辑器中很难看到或者找到函数名称。因此，有时会使用另一种代码风格：

struct key *
binsearch(char *word, struct key *tab, int n)

这是个人品味的问题；选择一种你喜欢的格式并坚持使用下去。【不要反复横跳】

6.5 自引用结构体

假定我们要处理更通用的问题：计算输入中所有单词的出现次数。由于不能事先知道单词列表，我们就无法方便地对其排序并使用二分搜索。而且我们不能在每个单词输入时，使用线性搜索来判断该单词是否已经出现过；否则程序会运行太久。（更准确地说，它的运行时间可能与输入的单词数量成平方关系。）我们要怎样组织数据，才能高效地处理一列任意单词呢？

一种解决方案，是使目前为止的所有单词都一直保持有序，即在每个单词输入时，都将它放到正确排序的位置上。然而，不应该通过在一个线性数组中移动单词来做到这一点——那也会太花时间。我们会使用一个叫做二叉树的数据结构来取而代之。

这棵树在每个“节点”上保存每个不同的单词；每个节点包含

指向单词文本的指针
单词的出现次数
指向左子节点的指针
指向右子节点的指针

任何节点都不能有超过两个的子节点；它只能有零个或一个子节点。

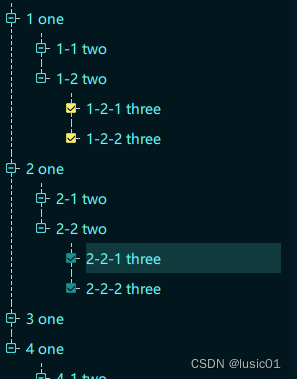
节点按这样的规则来维护：任意节点的左子树只包含字典序小于该节点单词的单词；而右子树只包含字典序大于该节点单词的单词。下图这棵树是由句子 “now is the time for all good men to come to the aid of their party” 构成的，每遇到一个单词就插入对应的节点（若是旧单词则更新节点的计数）。

为了判断一个新输入的词是否已经在树上，要从根节点开始，将新输入的词与节点中的词进行比较。如果匹配，则答案是肯定的。如果新词比树上的词小，则继续在左边的子节点搜索，否则在右边的子节点搜索。如果在对应的方向上没有子节点，说明新词不在树上，而此时，这个空位正好可以用来存放这个新词。这个过程是递归的，因为从任意节点开始的搜索，都会使用其子节点之一来搜索。因此，插入和打印也将非常自然地使用递归例程来实现。

回到节点的描述上来，用一个由四部分组成的结构体来表示它是很适合的：

struct tnode {             /* 树节点： */
    char *word;            /* 指向文本 */
    int count;             /* 出现次数 */
    struct tnode *left;    /* 左子节点 */
    struct tnode *right;   /* 右子节点 */
};

节点的递归声明看起来有问题，但它是正确的。在结构体中包含自身的实例是非法的，但是

struct tnode *left;

将 left 声明为 tnode 类型的指针，而不是 tnode 本身。

偶尔我们也会需要自引用结构体的变体：两个结构体互相引用。其处理方式为

struct t {
    ...
    struct s *p;    /* p 指向一个 s */
};
struct s {
    ...
    struct t *q;    /* q 指向一个 t */
};

因为已经有了一些支持例程（如我们之前所写的 getword），整个程序的代码量少的惊人。主例程使用 getword 读取每个单词，并使用 addtree 将其放到树上。

#include <stdio.h>
#include <string.h>
#include <ctype.h>

#define MAXWORD 100
struct tnode *addtree(struct tnode *, char *);
void treeprint(struct tnode *);
int getword(char *, int);

/* 单词频率计算 */
main()
{
    struct tnode *root;
    char word[MAXWORD];

    root = NULL;
    while (getword(word, MAXWORD) != EOF)
        if (isalpha(word[0]))
            root = addtree(root, word);
    treeprint(root);
    return 0;
}

函数 addtree 是递归的。单词由 main 给到树的顶级（根节点）。在每个阶段，单词都会与节点中已经保存的单词进行比较，然后通过对 addtree的递归调用，“渗透”到左边或者右边的子树上。最终，单词不是匹配到树中的某个节点（此时对计数器递增），就是遇到一个空指针，此时说明必须创建一个节点并加入到树上。如果创建了一个新节点，addtree 会返回指向它的指针，该指针需要被添加到父节点上。

struct tnode *talloc(void);
char *strdup(char *);

/* addtree: 在p的位置或其下层，加入带w的节点 */
struct tnode *addtree(struct tnode *p, char *w)
{
    int cond;

    if (p == NULL) {            /* 来了新词 */
        p = talloc();           /* 创建新节点 */
        p->word = strdup(w);
        p->count = 1;
        p->left = p->right = NULL;
    } else if ((cond = strcmp(p->word, w)) == 0)
        p->count++;            /* 重复单词 */
    else if (cond < 0)         /* 小于左子树 */
        p->left = addtree(p->left, w);
    else                       /* 大于右子树 */
        p->right = addtree(p->right, w);
    return p;
}

新节点的存储空间通过 talloc 例程获取，它返回一个指针，指向一段适合保存树节点的可用内存空间，而新单词通过 strdup 被拷贝到一个隐藏的内存空间。（我们很快会讲到这两个例程。）然后是初始化单词数量，并把两个子节点设为空。这部分代码只会在新节点加入时，在树的叶子节点上执行。我们（很不明智地）省略了对 stalloc 和 strdup 返回值的错误校验。

treeprint 有序地打印树；在每个节点上，它打印左子树（所有比当前节点单词小的），然后是当前节点上的单词，然后是右子树（所有比当前节点单词大的）。如果你对递归感觉不太有把握，可以模拟 treeprint 来打印前面显示的那棵树。

/* treeprint: 中序遍历树p */
void treeprint(struct tnode *p)
{
    if (p != NULL) {
        treeprint(p->left);
        printf("%4d %s\n", p->count, p->word);
        treeprint(p->right);
    }
}

实用性说明：如果由于单词不是随机进入而导致树“不平衡”，程序的运行时间可能会增长太多。最坏的情况下，如果单词都已经排过序了，那这个程序就会执行代价高昂的线性搜索。有文献论述了不会受到这种最坏情况影响的二叉树，但我们不在此描述【请自行深入研究】。

在结束这个例子之前，还值得简单讲下关于内存分配器问题的题外话。显然，理想的情况是一个程序里面只有一个内存分配器，即使这个程序会分配各种不同的对象。但如果一个分配器被用来处理，比如说 char 指针和 struct tnode 指针的请求，会出现两个问题。第一，它该如何满足大部分真实机器的要求，即某种类型的对象必须满足对齐限制（例如，整数必须位于偶数地址）？第二，声明要怎么写，才能处理一个分配器返回不同类型对象的指针的情况？

【第一个问题】对齐要求通常可以很容易满足，代价是浪费一些空间，即通过保证让分配器总是返回满足所有对齐限制的指针来做到。第五章的 alloc 函数不满足任何特定的对齐要求，因此我们这里会使用标准库函数 malloc，它当然是满足的。在第八章，我们会给出一种实现 malloc 的方案。

【第二个问题】如 malloc 这样的函数，它们的类型声明，是所有认真对待类型检查的语言都会遇到的烦人问题。在 C 中，正确的方法是把 malloc 声明为一个返回 void 指针的函数，然后显式地进行强制类型，转换为想要的类型。malloc 及其相关例程声明在标准库头文件<stdlib.h>中。因此 talloc 可以写成

#include <stdlib.h>

struct tnode *talloc(void)
{
    return (struct tnode *)malloc(sizeof(struct tnode));
}

strdup 仅仅是把参数传过来的字符串拷贝到一个安全的空间，后者通过调用 malloc 获取

char *strdup(char *s)    /* 复制s */
{
    char *p;

    p = (char *)malloc(sizeof(strlen(s)+1));  /* +1是给'\0'的 */
    if (p != NULL)
        strcpy(p, s);
    return p;
}

如果没有可用空间，则malloc 返回 NULL；strdup 把这个值往上传，让它的调用者来做错误处理。

调用 malloc 获取的空间可以自由地通过调用 free 释放，以供后续重复使用；见第七和第八章。