AI大语言模型学习笔记之三：协同深度学习的黑魔法

Transformer模型的崛起标志着人类在自然语言处理（NLP）和其他序列建模任务中取得了显著的突破性进展，而这一成就离不开GPU（图形处理单元）在深度学习中的高效率协同计算和处理。

Transformer模型是由Vaswani等人在2017年提出的，其核心思想是自注意力机制（self-attention mechanism），它在处理序列数据时能够捕捉长距离依赖关系，从而在NLP等任务中取得了优异的性能。

而GPU（图形处理单元）在这一突破性进展中发挥了重要作用。深度学习模型的训练通常需要大量的计算资源，而传统的中央处理单元（CPU）由于硬件架构的差异和并行处理性能的限制，在处理需要大量矩阵乘法和其他张量操作的高度并行深度学习任务时速度较慢。

在这里插入图片描述

而图形处理单元（GPU）是专门设计用于高度并行计算的专用芯片，特别适合加速深度学习任务。由于Transformer模型具有大量的参数，会对大规模的数据进行大量的高速并行计算和训练，GPU的并行处理能力就为大模型的训练提供了巨大的加速，因此更适合深度学习工作负载，使研究人员和工程师能够充分利用GPU的性能进行模型训练。
在这里插入图片描述

在训练大规模的Transformer模型时，使用GPU可以大幅缩短训练时间，加速模型的研发和部署过程。

因此，Transformer模型在NLP和序列建模任务中的成功与GPU的协同处理密不可分，为深度学习领域的发展和应用带来了显著的影响。

那么，在进行Transformer模型的深度学习任务时，GPU是如何运作的呢？下面我尝试通过一个简单的例子看看是否能够说明各个部件是如何协同工作的。

GPU在Transformer中的角色

Transformer 模型是一种基于自注意力机制的深度神经网络架构，其庞大的参数量和复杂的计算要求对计算机的计算能力的要求非常高。

我们知道目前使用的PC电脑或者服务器主要的计算处理模块都是CPU（中央处理单元），平常用来玩玩游戏、听听音乐、看电影、刷个剧不在话下，用来做专业设计、剪辑短视频、编辑文档、打印文件等工作也是得心应手。
在这里插入图片描述

之所以PC能干这么多不同的事情，主要是因为普通电脑的CPU（中央处理单元）在其架构设计时主要注重了多用途性能和通用的计算能力。CPU被设计成适用于各种任务，包括通用计算、图形界面处理、文件管理、音视频编码解码等。

而当我们进行 AI 深度学习任务时就不一样了。

深度学习的崛起引入了大规模的神经网络和复杂的模型结构，这导致了更多的参数和更复杂的计算图，通常涉及到大规模的矩阵乘法和张量运算，为了提升计算速度，这些操作通常是多个运算并行进行的，对计算机的并行能力提出了很高的要求。

诸如ChatGPT和GPT-4这样最先进的 AI 生成式预训练大语言模型涉及上万亿到上百万亿的参数和海量的数据，通常需要构建及其庞大的 AI GPU Cluster 集群才能满足计算、训练和推理需求，对 GPU 的计算能力要求更是堪称天花板级别的。
在这里插入图片描述

传统CPU虽然具有一些多核心，而且每个核心挺强的，但是数量确实少了点，难以满足深度学习大规模并行计算的需求。与此不同，现代GPU专注于大规模并行计算，拥有许多小型处理单元，使得它们在处理深度学习任务时更为高效。

就拿英特尔（Intel）和英伟达（NVIDIA）2023年各自发布的最新一代架构和核心处理器：
Intel® Xeon® Platinum 8593Q 和 NVIDIA H100 Tensor Core GPU 来说，核心数量和浮点运算性能对比如下：

第五代英特尔至强可扩展处理器

处理器	核心数量	FP64 FLOPS	FP32 FLOPS	TF32 FLOPS
Intel Xeon 8593Q CPU	64 核128 线程	5.04 TFLOPS (每秒5.04万亿次)	4.96 TFLOPS (每秒4.96万亿次)	4.94 TFLOPS (每秒4.94万亿次)
NVIDIA H100 GPU	18432 个 CUDA 核心 576个Tensor张量核心	60 TFLOPS (每秒60万亿次)	60 PFLOPS (每秒60万亿次)	1000 PFLOPS(每秒1000万亿次)

在这里插入图片描述

其中，FP64 表示双精度浮点运算，FP32 表示单精度浮点运算，TF32 表示混合精度浮点运算。

从上面的表格可以看出，NVIDIA H100 GPU 在 FP64 和 FP32 两个精度下的每秒浮点运算次数都比 Intel Xeon 8593Q 高出一个数量级（10倍）还要多，在 TF32 精度下的每秒浮点运算次数高出了约200多倍。这意味着 NVIDIA H100 GPU 在浮点计算方面具有明显的优势。

而传统的 CPU 架构在面对 AI 深度学习这种大数据量高并发张量计算时可能就显得力不从心，因为它们的设计更注重于处理多样化且频繁切换的任务,而非大规模数据的并行计算。

另外，深度学习框架和库通常会使用针对GPU设计的特定指令集和特殊优化，而这些优化使得GPU处理器更好地与深度学习任务协同工作。相较之下，CPU在这方面的优化可能比较有限，导致在同样进行深度学习任务时性能较慢。

因此，GPU 处理器在 Transformer 模型中的角色主要体现在其强大的并行计算能力，使得处理大规模、高度并行的深度学习任务变得高效和可行。这为深度学习在一系列自然语言处理（NLP）大模型和其他序列建模任务中的成功进展提供了重要的计算基础。

并行化的自注意力机制

Transformer中的自注意力机制（Self-Attention）是其核心组成部分之一，用于建立输入序列中每个元素与其他元素之间的关联。

为了更好的理解Transformer中的自注意力机制（Self-Attention），让我从一个简单的例子开始。假设你说了一句话：“我爱北京天安门”。我们想知道这句话中的每个词与其他词的关系。

在传统的自然语言处理（NLP）模型中，会将这句话的每个词转换为一个向量，然后使用这些向量来计算词与词之间的关系。例如，我们可以计算“我”与“爱”之间的关系。

在注意力计算（Attention Computation）中，查询向量 ( q ) 与输入序列 ( H = [h_1, h_2, …, h_n] ) 之间的计算用于权重分配，以便更加关注输入序列中与查询相关的部分。在机器翻译任务中，尤其是基于 Seq-to-Seq 模型的机器翻译任务，查询向量 ( q ) 通常是解码器（Decoder）端前一个时刻的输出状态向量。

我们考虑一个简化的注意力计算过程，其中使用了点积注意力（Dot-Product Attention）的形式：

$\text{Attention}(q, H) = \text{Softmax}\left(\frac{q \cdot H^T}{\sqrt{d}}\right) \cdot H \$

其中，( · ) 表示矩阵乘法， $H^T） \$ 表示输入序列的转置， $\ （\sqrt{d} ） \$ 用于缩放，以防止点积的数值过大。Softmax 函数用于将点积的结果转化为权重分布。

在机器翻译中，( q ) 可以是解码器的前一个时刻的隐藏状态，而 ( H ) 是编码器的所有隐藏状态。这样，计算得到的注意力权重将反映出解码器当前时刻对编码器各个时刻隐藏状态的关注程度。

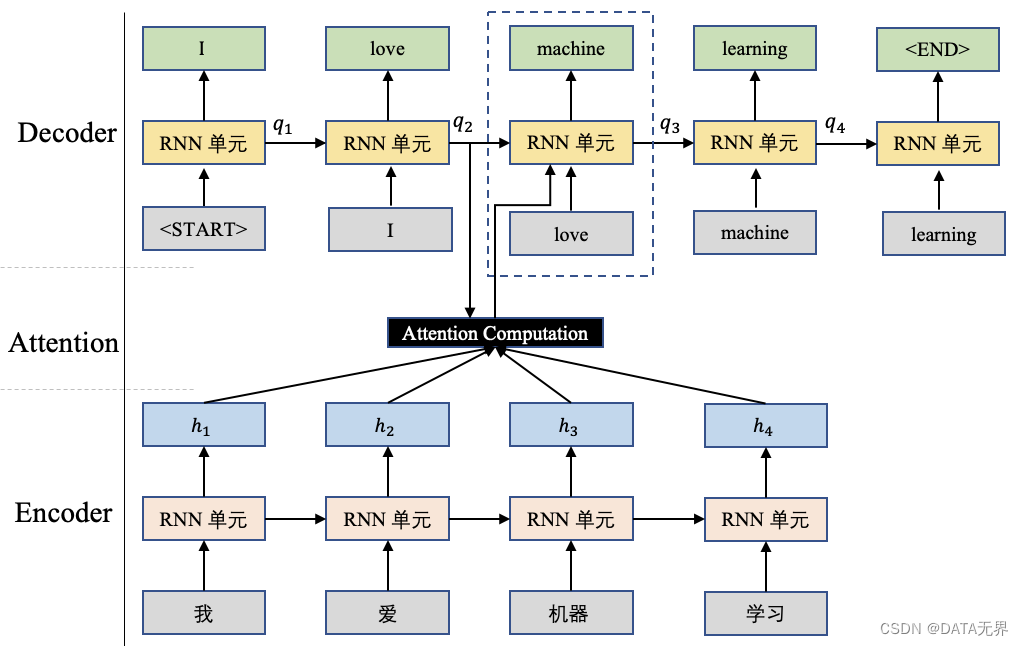
机器翻译示例图

通过将查询向量 ( q ) 与输入序列 ( H ) 进行点积计算，并使用 Softmax 函数生成权重分布，注意力机制使得模型能够自动关注输入序列中与当前解码器状态相关的部分，这对于更好地捕捉输入和输出序列之间的关联关系非常有帮助。

但是，这种方法存在一个问题。它假设每个词与其他词的关系都是相同的。例如，它假设“我”与“爱”的关系与“爱”与“北京”的关系相同。

自注意力机制（self-Attention）可以解决这个问题。它允许模型根据每个词的上下文来计算词与词之间的关系。

在我们的例子中，自注意力机制可以计算“我”与“爱”之间的关系，同时考虑“北京”和“天安门”这两个词。例如，它可以发现“我”与“爱”之间的关系更强，因为它们都是动词。

在自注意力机制中，采用了查询-键-值（Query-Key-Value）的机制，其中查询向量（Query vector）可以根据输入信息进行生成，而不是事先确定。

BERT（Bidirectional Encoder Representations from Transformers）是一个使用自注意力机制的预训练模型，下面让我们简要讨论BERT中的自注意力机制。

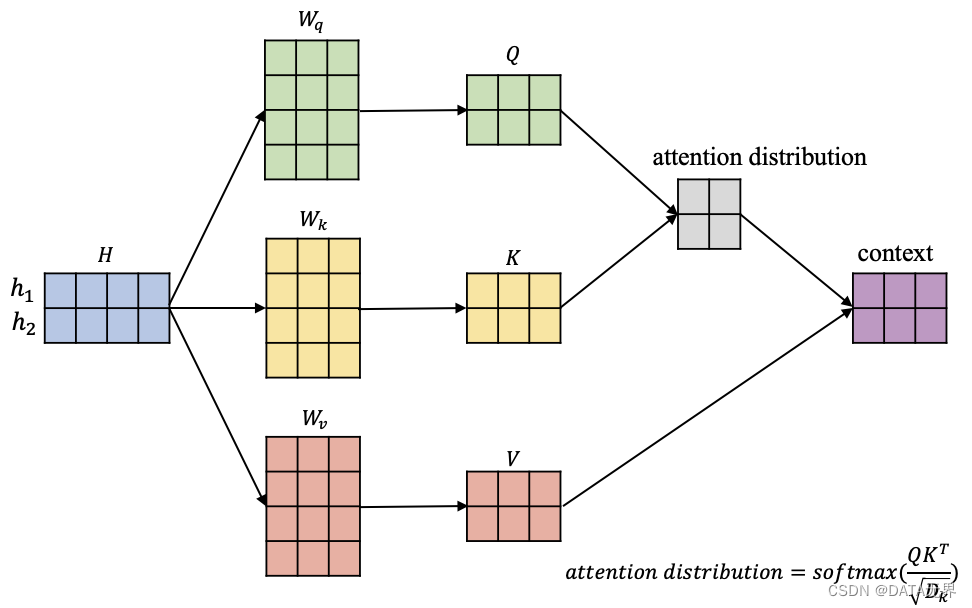
自注意力机制的计算过程

在上图中，我们有输入信息
$H = [h_1, h_2] \$
其中蓝色矩阵的每一行代表一个对应的输入向量。此外，图中还有三个矩阵
$W_q, W_k, W_v \$
它们负责将输入信息 ( H ) 依次转换到相应的查询空间
$Q = [q_1, q_2] \$
键空间
$K = [k_1, k_2] \$
值空间
$V = [v_1, v_2] \$
$\begin{align*} [q_1 = h_1W_q, q_2 = h_2W_q] & \Rightarrow Q = HW_q \\ [k_1 = h_1W_k, k_2 = h_2W_k] & \Rightarrow K = HW_k \\ [v_1 = h_1W_v, v_2 = h_2W_v] & \Rightarrow V = HW_v \\ \end{align*}$

在获得输入信息在不同空间的表示 ( Q, K, ) 和 ( V ) 后，我们以 ( h_1 ) 为例，计算这个位置的一个 attention 输出向量 ( \text{context}_1 )，它代表在这个位置模型应该重点关注的内容，如图3所示。

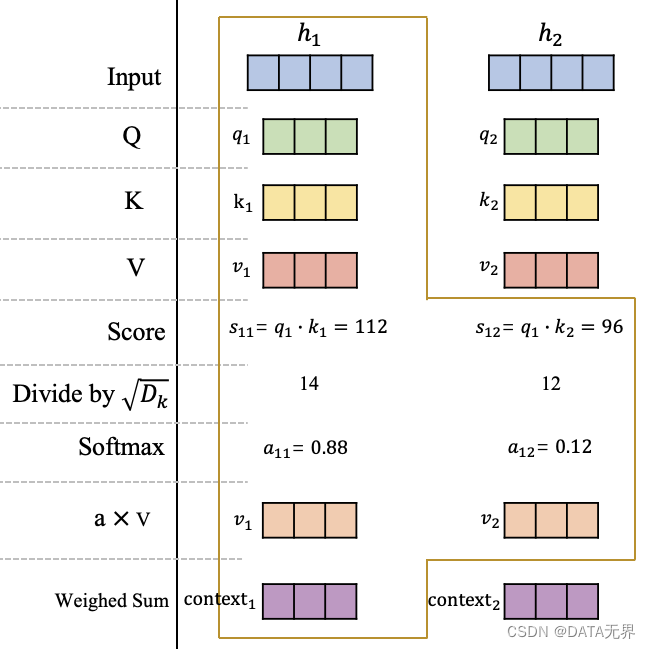
在这里插入图片描述

可以看到，在获得原始输入 ( H ) 在查询空间、键空间和值空间的表示 ( Q, K, ) 和 ( V ) 后，计算 ( q_1 ) 在 ( h_1 ) 和 ( h_2 ) 的分数 ( s_{11} ) 和 ( s_{12} )，这里的分数计算采用的是点积操作。

然后将分数进行缩放并使用 softmax 进行归一化，获得在 ( h_1 ) 这个位置的注意力分布： ( a_{11} ) 和 ( a_{12} )，它们代表模型当前在 ( h_1 ) 这个位置需要对输入信息 ( h_1 ) 和 ( h_2 ) 的关注程度。最后，根据该位置的注意力分布对 ( v_1 ) 和 ( v_2 ) 进行加权平均，获得最终在 ( h_1 ) 这个位置的 Attention 向量 ( \text{context}_1 )。

同理，可以获得第2个位置的 Attention 向量 ( \text{context}_2 )，或者继续扩展输入序列获得更多的 ( \text{context}_i )，原理都是一样的。

讨论到这里，相信你已经知道什么是注意力机制了，但为了更正式一点，我重新组织一下注意力机制的计算过程。

自注意力机制的计算过程可以分为以下几个步骤：

将每个词转换为一个向量。
计算每个词与其他词之间的相似度。
使用相似度来计算每个词的注意力权重。
使用注意力权重来加权每个词的向量。

最终，每个词都会得到一个加权后的向量，这个向量包含了该词与其他词的关系。

假设当前有输入信息 ( H = [h_1, h_2, …, h_n] )，我需要使用自注意力机制获取每个位置的输出

$\text{context} = [\text{context}_1, \text{context}_2, ..., \text{context}_n]$
首先，需要将原始输入映射到查询空间 ( Q )、键空间 ( K ) 和值空间 ( V )，相关计算公式如下：

$\begin{align*} Q & = HW_q = [q_1, q_2, ..., q_n] \\ K & = HW_k = [k_1, k_2, ..., k_n] \\ V & = HW_v = [v_1, v_2, ..., v_n] \\ \end{align*}$

接下来，计算每个位置的注意力分布，并将相应结果进行加权求和：

$\text{context}_i = \sum_{j=1}^n \text{softmax}(s(q_i, k_j)) \cdot v_j$

其中 ( s(q_i, k_j) ) 是经过上述点积、缩放后的分数值。

最后，为了加快计算效率，可以使用矩阵计算的方式，一次性计算出所有位置的 Attention 输出向量：

$\text{context} = \text{softmax}(QK^T/\sqrt{d})V$

这就是自注意力机制（self-Attention）的原理。

在进行自注意力计算时，GPU处理器的并行计算能力就可以大显身手了。以一个批次大小为64的例子为例，GPU处理器能够同时计算64个样本中每个样本的自注意力，加速整个模型的训练过程。

# 伪代码示例：Transformer中的自注意力计算
import torch
import torch.nn.functional as F

def self_attention(Q, K, V):
    attention_scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(Q.size(-1))
    attention_weights = F.softmax(attention_scores, dim=-1)
    output = torch.matmul(attention_weights, V)
    return output

# 在GPU上进行自注意力计算
Q_gpu = Q.to('cuda')
K_gpu = K.to('cuda')
V_gpu = V.to('cuda')

output_gpu = self_attention(Q_gpu, K_gpu, V_gpu)

这里，Q、K、V是输入序列的查询、键和值的表示，通过GPU上的矩阵乘法和softmax计算，同时处理多个样本的注意力权重。

多头注意力的并行化

Transformer模型中还引入了多头注意力机制，通过并行计算多个注意力头，提高了模型的表示能力。GPU处理器的并行计算能力极大地加速了多头注意力的计算，每个注意力头都可以在不同的GPU核心上独立计算。

# 伪代码示例：Transformer中的多头注意力计算
class MultiHeadAttention(torch.nn.Module):
    def __init__(self, num_heads, hidden_size):
        # 初始化多个注意力头
        self.attention_heads = [self_attention(Q, K, V) for _ in range(num_heads)]

    def forward(self, input):
        # 并行计算多个注意力头
        outputs = [attention_head(input) for attention_head in self.attention_heads]
        # 合并多个头的输出
        output = torch.cat(outputs, dim=-1)
        return output

# 在GPU上进行多头注意力计算
multihead_attention_gpu = MultiHeadAttention(num_heads=8, hidden_size=256).to('cuda')
output_gpu = multihead_attention_gpu(input_gpu)

在上述示例中，每个注意力头的计算可以独立地在GPU上进行，最后再通过GPU处理器的并行计算能力将它们合并。

CUDA流的优化

GPU通过CUDA流式处理的机制实现了高效的计算，这在Transformer模型的训练中尤为重要。例如，当进行反向传播时，GPU能够异步执行计算任务，从而实现数据的流水线处理，极大地提升了大模型的整体训练效率。

# 伪代码示例：反向传播过程中的CUDA流处理
loss.backward()
optimizer.step()

# 在GPU上异步执行计算任务
torch.cuda.synchronize()

上述代码中，反向传播和优化步骤进行了异步执行，通过torch.cuda.synchronize()等待计算完成，确保了计算的正确性。

GPU在Transformer 大模型中的协同计算处理任务中功不可没，其在架构和功能设计中体现出的强大的并行计算、流式处理和多头注意力的优势，堪称黑魔法，为AI 大模型的深度学习任务提供了强大的堪称黑魔法般的加持。

通过以上的例子来理解 GPU 在 Transformer 模型中的运行和处理机制，我们能够更加深入地体会深度学习和大语言模型这一魔法舞台的精彩。

正是在GPU的协同处理的魔法加持下，Transformer模型才得以在自然语言处理等领域创造出一系列令人瞩目的成果，极大地推进了诸如ChatGPT、Claude、Gemini、LLama、Vicuna 等杰出的生成式 AI 大模型的研究进展和部署应用。