文章目录
- 前言
- 那么什么是单源最短路 / 多源最短路呢?
- 如何解决此类题?
- 解法一
- 解法二
- 对于解法二,如何编写代码?
- 算法题
- 542.01矩阵
- 1020.飞地的数量
- 1765.地图中的最高点
- 1162.地图分析
前言
此前我们对 单源最短路 问题进行的讲解:
使用bfs算法解决单源最短路问题
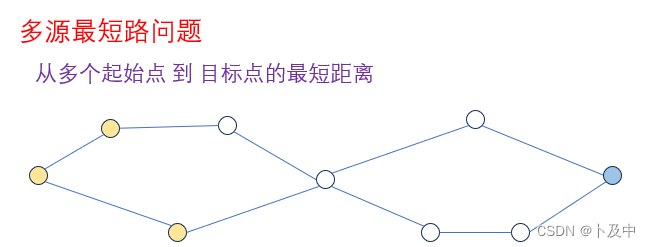
那么什么是单源最短路 / 多源最短路呢?
画图来说,单源最短路问题即为:
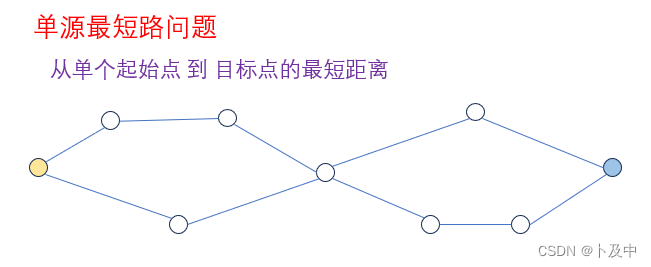
而对于多源最短路问题:
如何解决此类题?
自然是 利用BFS算法解决,下面提出解法:
解法一

解法二
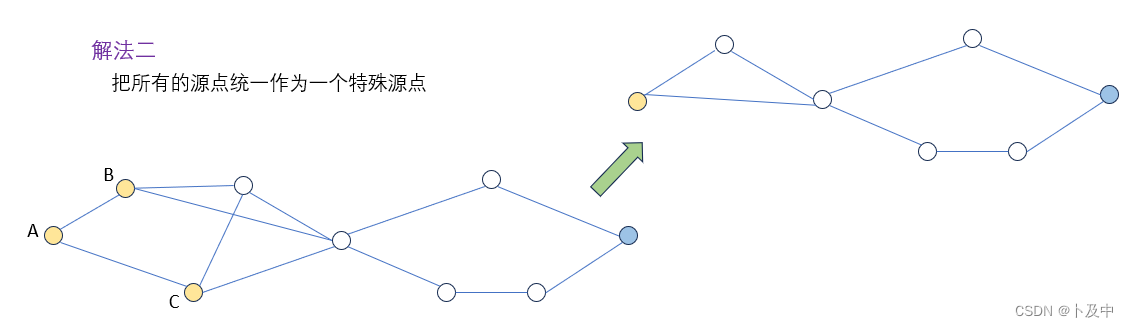
当我们将所有的源点作为一个源点来进行解题时,问题又变成了单源最短路问题,而为什么可以认为这种解法是正确的呢?
- 感性的理解 :对于上图的ABC三点,显然A点到目标点的距离更远,当我们将其作为一个点时,A点就会被直接排除,此时该特殊源点实际上就是最近的源点的合并。
对于解法二,如何编写代码?
我们对于 单源最短路 问题的bfs解法为:
- 将起始点加入到队列中,再进行一层一层的扩展
自然,对于 多源最短路 的bfs解法为:
- 将所有的起始点加入到队列中,再进行一层一层的扩展
算法题
542.01矩阵

思路
- 题意分析:题目要求返回一个数组,该数组的每一位都是矩阵中当前位置到最近的0的距离。这个数组我们叫做dist数组,下面多道题都会用上,
- 解法一: 对每个位置都进行扩展

- 解法二: bfs + 正难则反 + dist数组
- 正难则反:将思维逆转!我们以0作为起点,对矩阵进行扩容
- dist数组:也是结果数组,开始初始化为-1,对于dist[i][j]:
dist[i][j] == -1:未被检索过dist[i][j] != -1:该位置到0的最短距离
- 将矩阵的所有起始点0的位置加入矩阵
- 根据下图的思路,每次对队列中的元素进行扩展

代码
class Solution {
public:
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0 ,0};
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1)); // 将dist数组元素初始化为-1(未检索的状态)
queue<pair<int, int>> q;
// 正难则反:以矩阵中的0作为起点进行扩展
// 将所有起始点入队
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(mat[i][j] == 0)
{
q.push({i, j});
dist[i][j] = 0;
}
// 对队列中的元素进行拓展
while(q.size())
{
auto [a, b] = q.front(); q.pop();
for(int i = 0; i < 4; ++i)
{
int x = dx[i] + a, y = dy[i] + b;
if((x >= 0 && x < m) && (y >= 0 && y < n) && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
}
}
}
return dist;
}
};
1020.飞地的数量
思路
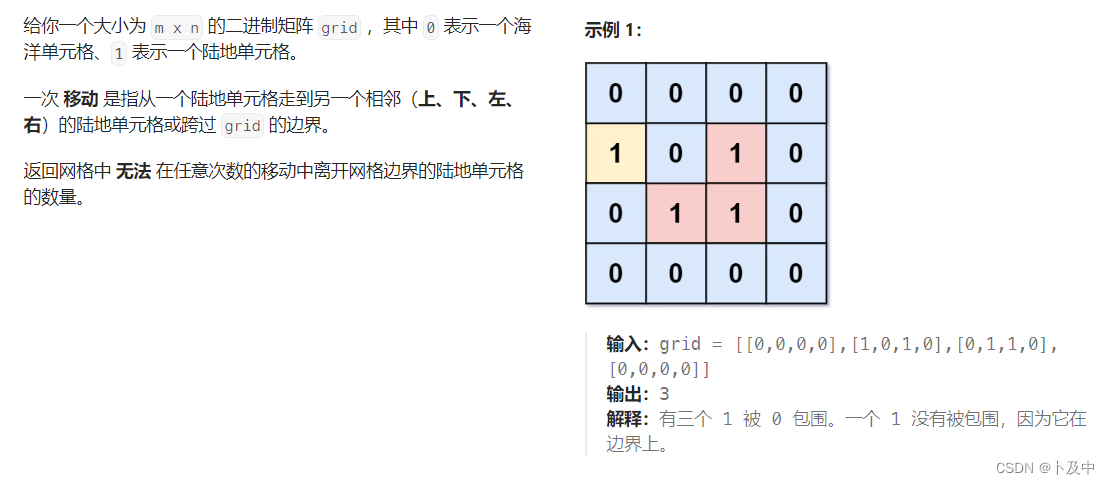
- 题意分析:题目要求返回无法离开水域的陆地单元格个数,即在边界内且被水域完全包裹的单元格。
- 解法: bfs + 正难则反
- 正难则反:我们以四边的1为起点,向内扩展
- 多源bfs:将四边的1作为起点入队,将相连接的陆地单元格标记
- 最后遍历visited数组,统计结果
代码
class Solution {
public:
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
int numEnclaves(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
// 将visited数组元素初始化为0
vector<vector<bool>> visited(m, vector<bool>(n, false));
queue<pair<int, int>> q;
// 正难则反:以边界的1为起始点,进行bfs
// 1. 找到边界1,并扩展
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(((i == 0 || i == m-1) || (j == 0 || j == n-1)) && grid[i][j] == 1)
{
q.push({i, j});
visited[i][j] = true;
}
// 2. 多源bfs
while(q.size())
{
auto [a, b] = q.front(); q.pop();
for(int i = 0; i < 4; ++i)
{
int x = a + dx[i], y = b + dy[i];
if((x >= 0 && x < m) && (y >= 0 && y < n) && !visited[x][y] && grid[x][y])
{
q.push({x, y});
visited[x][y] = true;
}
}
}
// 3. 提取结果
int ret = 0;
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(!visited[i][j] && grid[i][j])
++ret;
return ret;
}
};
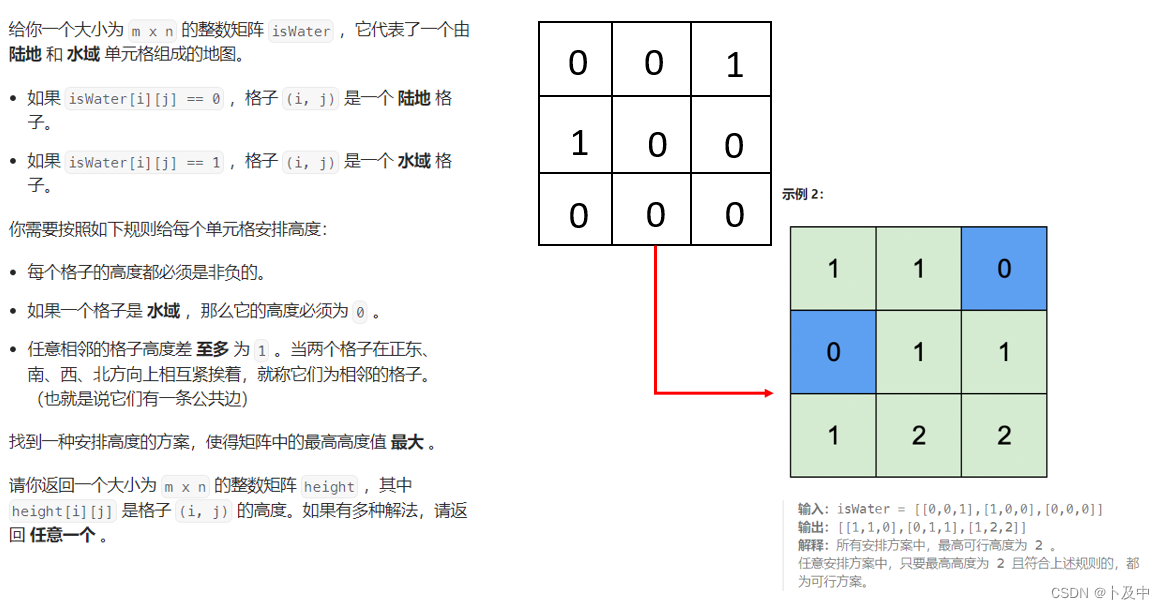
1765.地图中的最高点
思路
- 题意分析:题目给出一个矩阵,1为水域,0为陆地,要求我们自行安排陆地高度,使矩阵的最高高度最大(相邻单元格高度差 <= 1)
- 解法: bfs + dist数组
- 思路:
- 首先创建dist数组,原理与第一题01矩阵一样,将矩阵中所有水域的位置在dist中初始化为0,并插入到队列中。
- 由于要求矩阵的最高高度最大,我们在设计高度时自然要将高度差都设为最大值,即1
- 随后进行多源bfs的操作,综上我们发现,这道题理清思路后,代码方面和“01矩阵”完全一致
代码
class Solution {
public:
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
// 思路同 “10矩阵”
int m = isWater.size(), n = isWater[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1));
queue<pair<int, int>> q;
// 1.对水域进行扩展
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(isWater[i][j] == 1) // 1是水域
{
q.push({i, j});
dist[i][j] = 0;
}
// 2.
while(q.size())
{
auto [a, b] = q.front(); q.pop();
for(int i = 0; i < 4; ++i)
{
int x = a + dx[i], y = b + dy[i];
if((x >= 0 && x < m) && (y >= 0 && y < n) && dist[x][y] == -1)
{
q.push({x, y});
dist[x][y] = dist[a][b] + 1;
}
}
}
return dist;
}
};
1162.地图分析

思路
-
题意分析:题目要求找到离陆地最远的海洋单元格的曼哈顿距离, 曼哈顿距离 简单解释为:

-
解法思路: bfs + 正难则反 + dist数组
- 正难则反:题目要求找海洋到陆地的最大距离,我们以陆地单元格作为起始点,向内扩展
- 同样的思路,我们首先遍历数组,将陆地单元格位置存入到队列中,并标记dist的位置
- 后执行多源bfs的代码思路即可
代码
class Solution {
public:
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
int maxDistance(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
// 正难则反:以1为起点,向内扩展并标记
vector<vector<int>> dist(m, vector<int>(n, -1));
queue<pair<int, int>> q;
// 1. 根据单元格1向内扩展
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(grid[i][j] == 1)
{
q.push({i, j});
dist[i][j] = 0;
}
// 2. 多源bfs
int ret = -1; // 统计结果
while(q.size())
{
auto [a, b] = q.front(); q.pop();
for(int i = 0; i < 4; ++i)
{
int x = a + dx[i], y = b + dy[i];
if((x >= 0 && x < m) && (y >= 0 && y < n) && dist[x][y] == -1)
{
q.push({x, y});
dist[x][y] = dist[a][b] + 1;
ret = max(ret, dist[x][y]);
}
}
}
return ret;
}
};