一、图
(一)图是什么
图是网络结构的抽象模型,是一组由边连接的节点。图可以表示任何二元关系,比如道路、航班…
JS中没有图,但是可以用 Object 和 Array 构建图。图的表示法:邻接矩阵、邻接表…
1、邻接矩阵:用矩阵表示节点之间是否存在连接关系
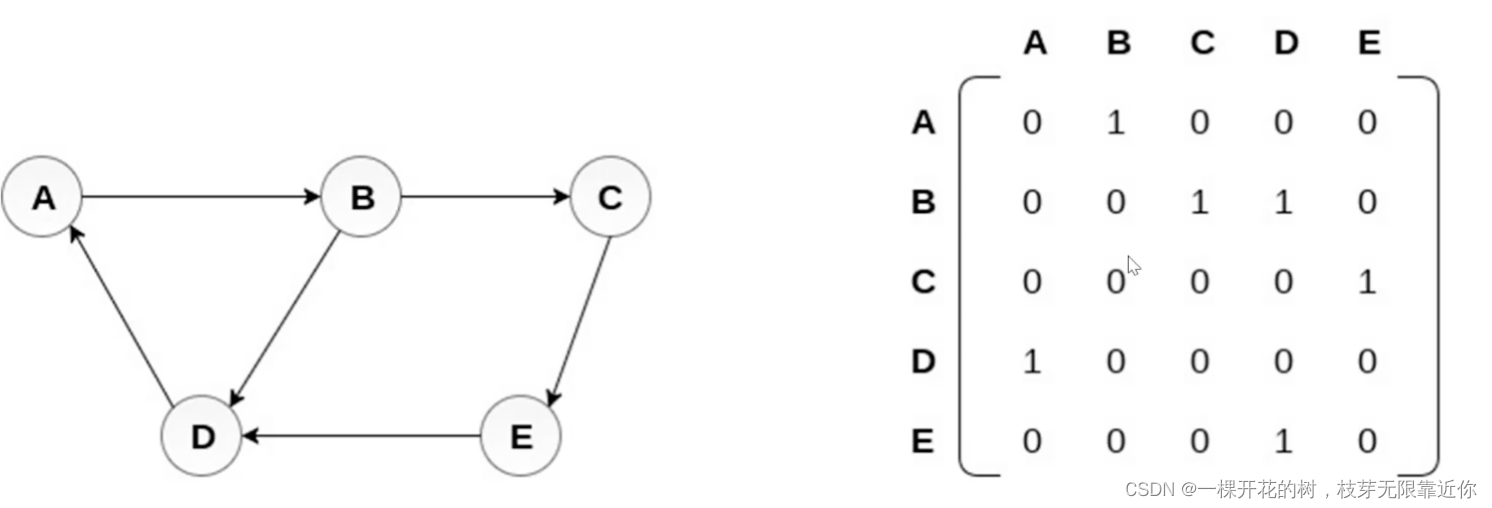
2、邻接表:用对象和数组表示一个节点都和哪个节点有链接,还可以用链表等表示
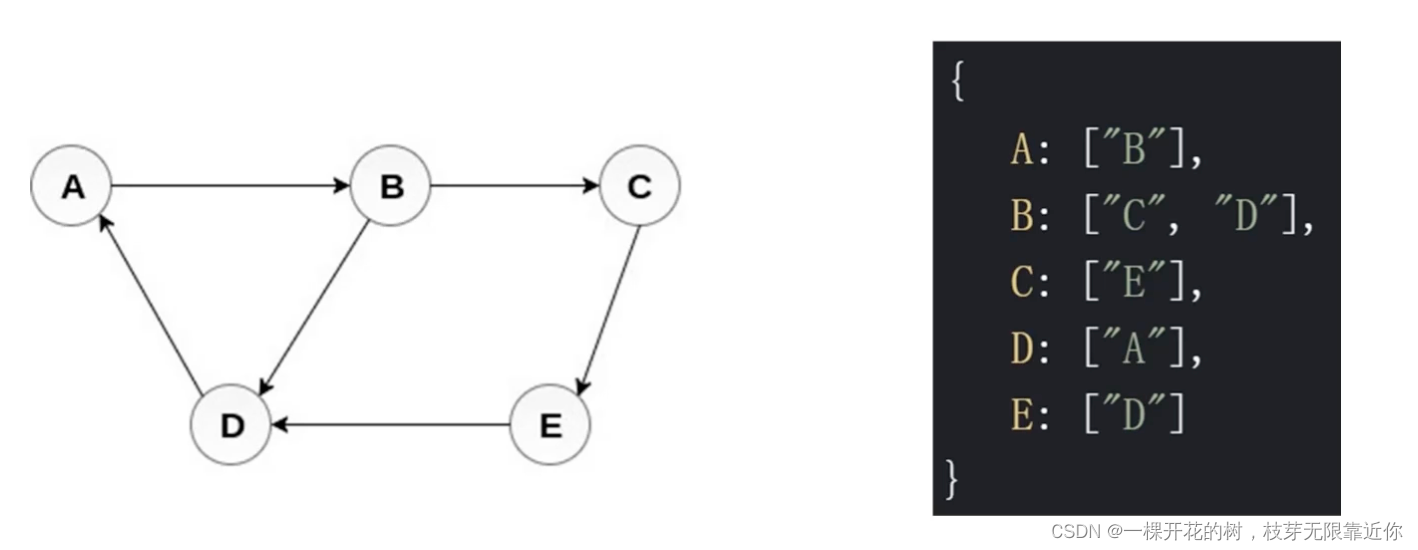
(二)图的常用操作
-
深度优先遍历:尽可能深的搜索图的分支。
深度优先遍历算法口诀
① 访问根节点。
② 对根节点的没访问过的相邻节点挨个进行深度优先遍历。
由于图中节点的连接关系可能是双向的,所以在访问之前要先判断是否已经访问过,否则就会在两个相互连接的节点之间来回访问。
先创建一个可以共用的图,并且导出const graph = { 0: [1, 2], 1: [2], 2: [0, 3], 3: [3] } module.exports = graph;// 深度优先遍历 const gragh = require('./gragh') // 记录访问过的节点 let visited = new Set() const dfs = n =>{ // 访问当前节点 console.log(n) visited.add(n) // 没有访问过的相邻节点再进行深度优先遍历 gragh[n].forEach(item=>{ if(!visited.has(item)){ dfs(item) } }) } dfs(2)输出结果:

-
广度优先遍历:先访问离根节点最近的节点。
广度优先遍历算法口诀
① 新建一个队列,把根节点入队。
② 把队头出队并访问。
③ 把队头的没访问过的相邻节点入队。
④ 重复第二、三步,直到队列为空。const gragh = require('./gragh') const visited = new Set(); const bfs = n => { // 创建队列 let queue = [n]; // 队头直接加进去 visited.add(n) while (queue.length > 0) { // 访问队头并出队 const head = queue.shift() console.log(head) // 没有访问过的相邻节点再进行深度优先遍历 gragh[head].forEach(item => { if (!visited.has(item)) { queue.push(item) // 只要入队就加入visited,避免下次再push visited.add(item) } }) } } bfs(2)输出结果:

二、堆
(一)堆是什么
-
堆是一种特殊的完全二叉树。每层节点都完全填满,如果最后一层不满,则只缺少右节点
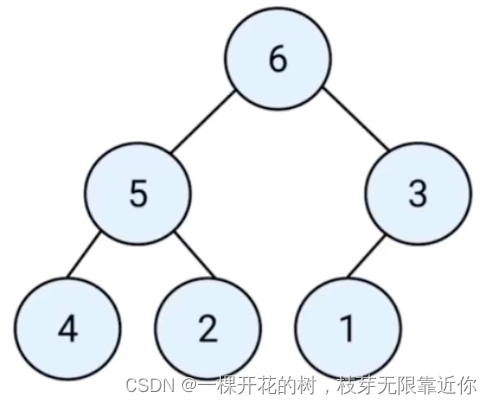
-
所有的节点都大于等于(最大堆)或小于等于(最小堆)它的子节点。
-
js中的堆:通常使用数组表示堆
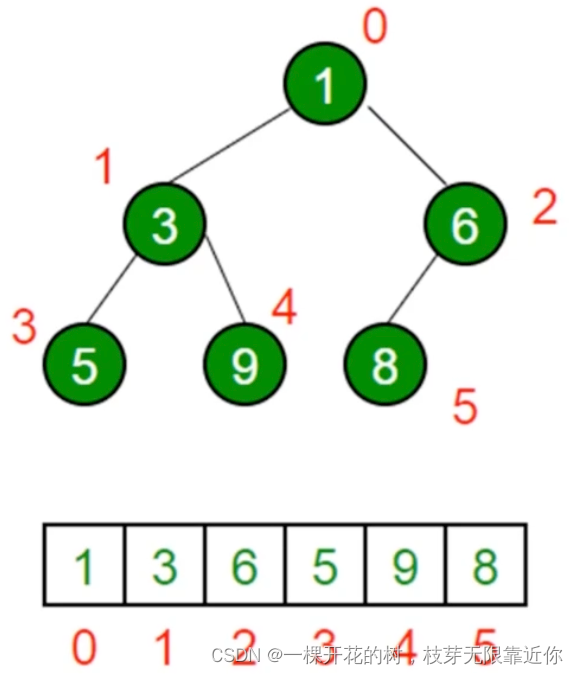
我们可以使用一些总结出来的公式来计算节点的位置:
1、索引为index的节点的左侧子节点的位置是 2index+ 1
2、索引为index的节点的左侧子节点的位置是 2index+ 2
3、索引为index的节点的父节点位置是 (index- 1)/2 的商 -
堆的应用
堆能高效、快速地找出最大值和最小值,它的时间复杂度:0(1)。
找出第K个最大(小)元素。
例:求第K个最大元素
① 构建一个最小堆,并将元素依次插入堆中。
② 当堆的容量超过 K,就删除堆顶。
③ 插入结束后,堆顶就是第K 个最大元素。
最小堆的堆顶元素是堆的最小值
(二)js实现最小堆类
实现最小堆类主要是要实现堆的四个功能,其实就类似于数组
1、插入元素
2、删除堆顶
3、获取堆顶
4、获取堆的长度
// 最小堆类
class MinHeap {
constructor() {
// 用数组模拟堆
this.heap = [];
}
// 交换两个索引位置的值
swap(i1, i2) {
const temp = this.heap[i1]
this.heap[i1] = this.heap[i2]
this.heap[i2] = temp
}
// 获取父节点的index
getParantIndex(i) {
// 二进制的操作,把二进制的数字往右边移动一位
// 就是除以2得到的商
return (i - 1) >> 1
}
// 获取左侧子节点
getLeftIndex(i) {
return i * 2 + 1;
}
// 获取右侧子节点
getRightIndex(i) {
return i * 2 + 2
}
// 上移
shiftUp(index) {
// 如果上移到了堆顶,就结束上移
if (index == 0) return;
// 上移操作
const parentIndex = this.getParantIndex(index);
// 比较父节点和当前节点谁大
if (this.heap[parentIndex] > this.heap[index]) {
this.swap(parentIndex, index)
this.shiftUp(parentIndex)
}
}
// 下移
shiftDown(index) {
// 如果下移到了堆底则结束下移
if (index == this.heap.length - 1) return;
// 左子节点
const leftIndex = this.getLeftIndex(index)
if(this.heap[leftIndex]<= this.heap[index]){
this.swap(leftIndex, index)
this.shiftDown(leftIndex)
}
// 右子节点
const rightIndex = this.getRightIndex(index)
if(this.heap[rightIndex]<= this.heap[index]){
this.swap(rightIndex, index)
this.shiftDown(rightIndex)
}
}
// 一、插入元素
// 1 插入到堆的底部,即数组的尾部
// 2 然后上移:将这个值和它的父节点进行交换,直到父节点小于等于这个插入的值。
// 3 大小为 k 的堆中插入元素的时间复杂度为 O(logk)。
// 因为上移操作最多移动的次数就是堆的高度。所以时间复杂度是 O(logk)
insert(value) {
this.heap.push(value);
this.shiftUp(this.heap.length - 1)
}
// 二、删除堆顶
// 1 用数组尾部元素替换堆顶(直接删除堆顶,后面所有的元素会往前移动一位,会破坏堆结构)。
// 2 然后下移:将新堆顶和它的子节点进行交换,直到子节点大于等于这个新堆顶。
// 3 大小为k的堆中删除堆顶的时间复杂度为 O(logk)。
pop() {
this.heap[0] = this.heap.pop();
this.shiftDown(0)
}
// 三、获取堆顶
// 直接返回数组的头部
peek(){
return this.heap[0]
}
// 四、获取堆的长度
size(){
return this.heap.length
}
}
三、搜索排序算法
排序:把某个乱序的数组变成升序或者降序的数组。
搜索:找出数组中某个元素的下标。
js中的排序:sort()
js中的搜索:indexOf()
虽然javascript中提供的有现成的排序和搜索的方法,但是其中的实现原理也是值得我们深入学习的
排序算法常见的有以下几种·:
冒泡排序
选择排序
插入排序
归并排序
快速排序
搜索算法常见的有以下几种:
顺序搜索
二分搜索
(一)排序算法
1、冒泡排序
① 比较所有相邻元素,如果第一个比第二个大,则交换它们。
② 一轮下来,可以保证最后一个数是最大的。
③ n-1 轮下来,可以实现正序排列
冒泡排序需要进行两次for循环,时间复杂度是O(n的二次方)
// 冒泡排序
Array.prototype.bubbleSort = function () {
// 数组执行bubbleSort()方法的时候,this指向数组本身
for (let i = 0; i < this.length - 1; i++) {
for (let j = 0; j < this.length - 1 -i; j++) {
if (this[j] > this[j + 1]) {
[this[j], this[j + 1]] = [this[j + 1], this[j]]
}
}
}
}
2、选择排序
① 找到数组中的最小值,选中它并将其放置在第一位。
② 接着找到第二小的值,选中它并将其放置在第二位。
③ 以此类推,执行n-1轮。
// 选择排序
// 时间复杂度 两个嵌套循环 O(n的二次方)
Array.prototype.selectionSort = function () {
// 遍历元素,标记最小值
// 将最小值和数组的第一个元素进行交换
for (let i = 0; i < this.length - 1; i++) {
// i之前的元素都已经按从小到大的顺序排好了,只需要从i开始寻找最小值
let indexMin = i;
for (let j = i; j < this.length; j++) {
if (this[j] < this[indexMin]) {
indexMin = j
}
}
// 如果最小值不是第一个元素才需要交换
if (indexMin != i) [this[indexMin], this[i]] = [this[i], this[indexMin]]
}
}
4、插入排序
① 从第二个数开始往前比。
② 遇到比它大的数就往后面移动一位。例如下图,发现第一个数字是 46,第二个数字是44,就把第一个数字往后移动一位,和后面的数字交换数值
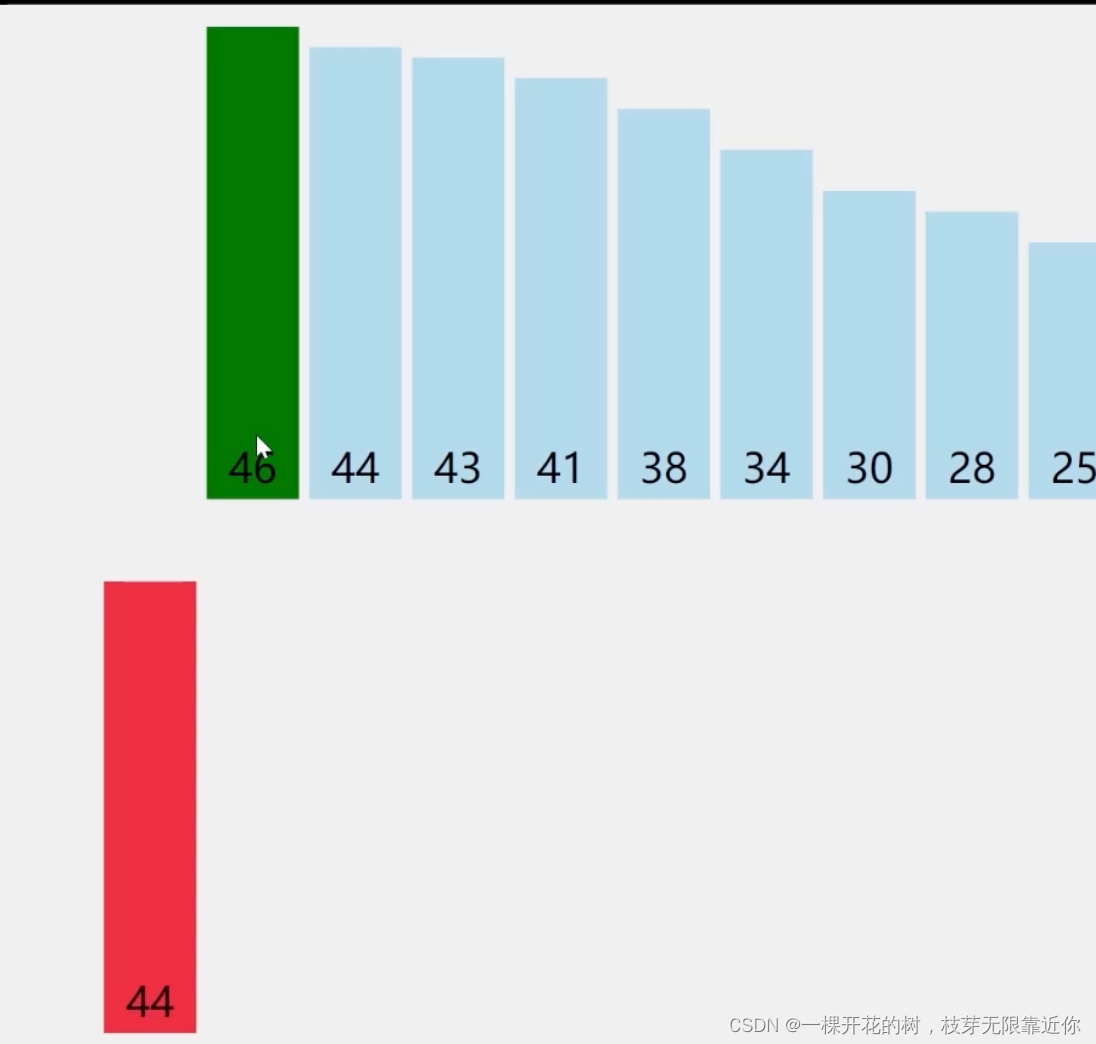
一直往前找,只要比当前数字大,就往后移动一位
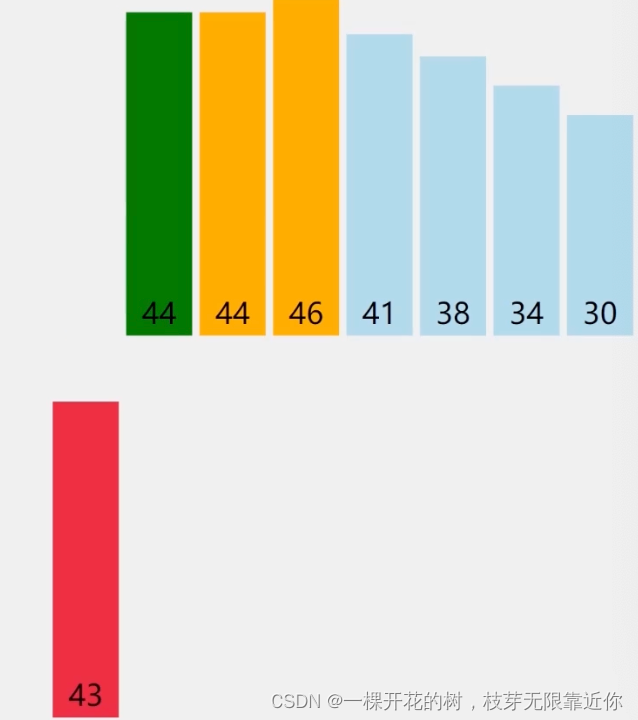
③ 以此类推进行到最后一个数。
// 插入排序
// 时间复杂度 O(n的二次方)
Array.prototype.insertSort = function () {
// 先考虑第一次比较
// 从第二个数开始往前比
for (let i = 1; i < this.length; i++) {
const temp = i;
// 用j来表示往前找最小值找到的下标
let j = i;
while (j > 0) {
if (this[j - 1] > temp) {
this[j] = this[j - 1]
} else {
break
}
j -= 1;
}
// j就是要插入的位置并且原来的元素已经往后移动了
this[j] = temp
}
console.log(this)
}
4、归并排序
性能比前几种逗号
① 分:把数组劈成两半,再递归地对子数组进行“分”操作,直到分成一个个单独的数。
② 合:把两个数合并为有序数组,再对有序数组进行合并,直到全部子数组合并为一个完整数组。
合并有序数组:
① 新建一个空数组res,用于存放最终排序后的数字
② 比较两个有序数组的头部,较小者出队并推入res中。
③ 如果两个数组还有值,就重复第二步。
// 归并排序
// 时间复杂度:
// 分的时间复杂度是O(logn)
// 合的时间复杂度是O(n)
// 由于分和合是嵌套关系,所以整体的时间复杂度是O(n*logn)
Array.prototype.mergeSort = function () {
// 将所有元素分成单个元素的数组
const rec = (arr) => {
if (arr.length <= 1) {
// 此时的arr就已经是单个元素的数组的
return arr;
}
// 从中间开始劈成两半
const mid = Math.floor(arr.length / 2)
const left = arr.slice(0, mid)
const right = arr.slice(mid, arr.length)
// 单独的元素组成的数组
const orderLeft = rec(left)
const orderRight = rec(right)
// 合并两个有序数组
const res = []
while (orderLeft.length || orderRight.length) {
if (orderLeft.length && orderRight.length) {
// 找两个有序数组中头部更小的数组
// 将这个数组的头推出,并且push到res里面
res.push(orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift())
} else if(orderLeft.length) {
// 如果orderLeft还有值,就将orderLeft中的元素不断推出并push进res
res.push(orderLeft.shift())
}else if(orderRight.length) {
res.push(orderRight.shift())
}
}
return res
}
const res = rec(this)
// // 把res上面的值copy到this上
res.forEach((n,i)=>this[i] = n)
}
5、快速排序
① 分区:从数組中任意选择一个 “基准”,所有比基准小的元素放在基准前面,比基准大的元素放在基准的后面。
② 递归:递归地对基准前后的子数组进行分区。
// 时间复杂度
// 递归的时间复杂度是 O(logn)
// 分区的时间复杂度是 O(n)
// 总体的时间复杂度是 O(n*logn)
Array.prototype.quickSort = function () {
// 也需要递归,先创建一个递归方法
const rec = (arr) => {
if (arr.length <= 1) {
return arr;
}
// 创建left和right分别存放比基准小和比基准大的元素
const left = [];
const right = [];
// 基准元素设置为第一个元素
const mid = arr[0]
for (let i = 1; i < arr.length; i++) {
if (arr[i] < mid) {
left.push(arr[i])
} else {
right.push(arr[i])
}
}
return [...rec(left), mid, ...rec(right)]
}
const res = rec(this);
res.forEach((n,i)=>{
this[i] = n
})
}
(二)搜索算法
1、顺序搜索
顺序搜索是最基本的搜索,比较低效
① 遍历数组。
② 找到跟目标值相等的元素,就返回它的下标。
③ 遍历结束后,如果没有搜索到目标值,就返回-1。
// 顺序搜索
// 时间复杂度 O(n)
Array.prototype.sequentialSearch = function (target){
for(let i=0;i<this.length;i++){
if(this[i] == target) return i
}
return -1
}
2、二分搜索
① 从数组的中间元素开始,如果中间元素正好是目标值,则搜索结束。
② 如果目标值大于或者小于中间元素,则在大于或小于中间元素的那一半数组中搜索。
// 二分搜索
// 时间复杂度 每一次比较都使搜索范围缩小一半 O(logn)
// 假设数组是有序的
Array.prototype.binarySearch = function (target) {
// 搜索范围中的最小下标
let low = 0;
// 搜索范围中的最大下标
let high = this.length - 1;
while (low <= high) {
// 找中间索引
const mid = Math.floor((low + high) / 2)
const element = this[mid]
if (element < target) {
// 说明目标值在数值比较大的那一半里面
low = mid + 1;
} else if (element > target) {
high = mid - 1
}else{
return mid
}
}
return -1
}
四、算法设计思想
这一章是讲解决问题的方法、思路
(一)分而治之
① 分而治之是算法设计中的一种方法。
⑤ 它将一个问题分成多个和原问题相似的小问题,递归解决小问题,再将结果合并以解决原来的问题。
- 场景一:归并排序
✳️ 分:把数组从中间一分为二。
✳️ 解:递归地对两个子数组进行归并排序。
✳️ 合:合并有序子数组。 - 场景二:快速排序
✳️ 分:选基准,按基准把数组分成两个子数组。
✳️ 解:递归地对两个子数组进行快速排序。
✳️ 合:对两个子数组进行合并。
(二)动态规划
① 动态规划是算法设计中的一种方法。
② 它将一个问题分解为相互重叠的子问题,通过反复求解子问题,来解决原来的问题。
”动态规划“强调把问题分解为相互重叠的子问题,而”分而治之“强调把问题分解为相互独立的子问题
相互重叠的含义:子问题之间不会相互独立的,需要依赖其他子问题的结果
举一个例子帮助理解什么是相互重叠的子问题:斐波那契数列

其实就类似于数学里面的找规律,当前节点的解决依赖于前一个节点的解决
1、定义子问题:F(n) = F(n-1) + F(n-2)。
2、反复执行:从2循环到n,执行上述公式。
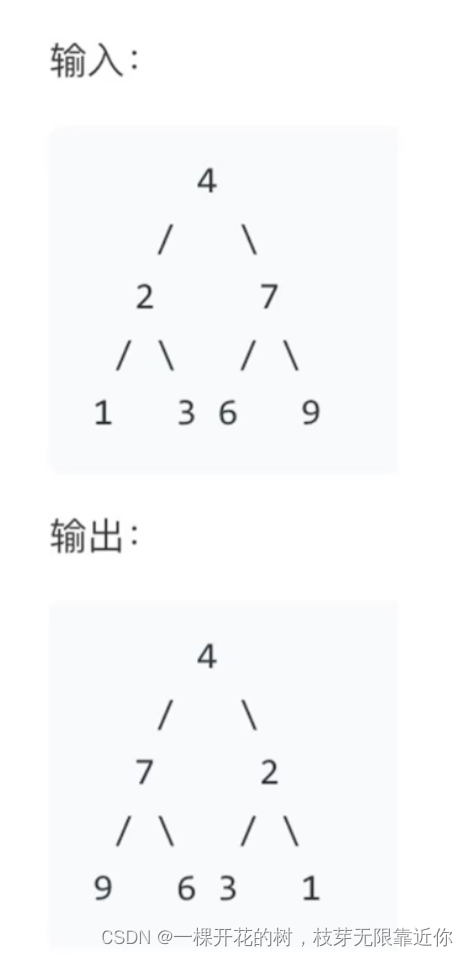
相互独立的含义:子问题之间没有任何关系,是独立的问题,例如翻转二叉树,拆分为翻转左子树和翻转右子树这两个问题,这两个问题之间没有任何关系
(三)贪心算法
① 贪心算法是算法设计中的一种方法。
② 期盼通过每个阶段的局部最优选择,从而达到全局的最优。
③ 结果并不一定是最优。
举个🌰帮助理解:

上面这道题coins给出了零钱的所有面值,以及要兑换的总额amount,求解最少需要几个零钱。如果使用贪心算法,每一步都使用可选择的最大面值,那么可能就不是最优解,比如第二种情况,选择两个3才是最优解
虽然贪心算法并不是在所有情况下都能得到最优解,但是有一些题目就比较适合使用贪心算法求解,以下题目:
力扣:455 分饼干; 122 买卖股票的最佳时机 II
(四)回溯算法
① 回潮算法是算法设计中的一种方法。
② 回溯算法是一种渐进式寻找并构建问题解决方式的策略。
③ 回潮算法会先从一个可能的动作开始解決问题,如果不行,就回潮并选择另一个动作,直到将问题解決。
就像在岔路口选择一条正确的路,先选一条路走一走,如果不行,就回到岔路口选另一条
什么问题适合用回溯算法来解决?
1、有很多路(路就是序列)
2、其中有死路也有活路
3、要用到递归
例如全排列问题