目录
- 1.系数矩阵
- 2.高斯消元法
- 3.置换矩阵 Permutation
- 4.逆矩阵 Inverse
- 5.高斯-若尔当消元法
- 6.矩阵的 LU 分解
- 7.三角矩阵
- 8.正定矩阵
1.系数矩阵
线性代数的基本问题就是解 n 元一次方程组。例如:二元一次方程组
2
x
−
y
=
0
−
x
+
2
y
=
3
\begin{align*} & 2x - y= 0\\ & -x+2y = 3 \end{align*}
2x−y=0−x+2y=3
写成矩阵形式就是 :
[
2
−
1
−
1
2
]
[
x
y
]
=
[
0
3
]
\begin{bmatrix} 2&-1\\-1&2 \end{bmatrix}\begin{bmatrix} x\\y \end{bmatrix}=\begin{bmatrix} 0\\3 \end{bmatrix}
[2−1−12][xy]=[03]
其中 A=
[
2
−
1
−
1
2
]
\begin{bmatrix} 2&-1\\-1&2 \end{bmatrix}
[2−1−12]被称为系数矩阵(coefficient matrix)。 未知数向量通常记为 x=
[
x
y
]
\begin{bmatrix} x\\y \end{bmatrix}
[xy],而等号右侧的向量记为 b。线性方程组简记为 Ax=b。
2.高斯消元法
消元法是计算机软件求解线形方程组所用的最常见的方法。任何情况下,只要是矩阵 A 可逆,均可以通过消元法求得 Ax=b 的解。
高斯消元法(Gauss elimination)就是通过对方程组中的某两个方程进行适当的数乘和加(jian)和(fa),以达到将某一未知数系数变为零,从而削减未知数个数的目的。
3.置换矩阵 Permutation
置换矩阵,是一种特殊的方阵,其中每行和每列只有一个元素为1,其他元素都为0。它表示了对向量或矩阵的行或列的置换操作。

置换矩阵的逆矩阵即为它的转置
P
−
1
=
P
T
P^{-1}=P^T
P−1=PT。
置换矩阵 P 是通过对单位阵进行“行交换”得到的。对于 n x n 矩阵存在着 n!个置换矩阵。置换矩阵具有特殊性质
P
−
1
=
P
T
P^{-1}=P^T
P−1=PT 即
P
T
P
=
I
P^TP=I
PTP=I。
4.逆矩阵 Inverse
逆矩阵,也称为反矩阵,是指一个方阵A的逆矩阵
A
−
1
A^{-1}
A−1,它满足以下条件:
A
和
A
−
1
A和A^{-1}
A和A−1是方阵。
A
乘以
A
−
1
等于单位矩阵
I
:
A
A
−
1
=
A
−
1
A
=
I
A乘以A^-1等于单位矩阵I:A A^{-1} = A^{-1} A = I
A乘以A−1等于单位矩阵I:AA−1=A−1A=I。
A
−
1
唯一存在,当且仅当
A
是可逆矩阵
A^{-1}唯一存在,当且仅当A是可逆矩阵
A−1唯一存在,当且仅当A是可逆矩阵。
如果矩阵 A 是方阵,若存在逆矩阵 A − 1 A^{-1} A−1,使得 A − 1 A = I = A A − 1 A^{-1}A=I=A A^{-1} A−1A=I=AA−1(左逆矩阵等于右逆矩阵)。我们称矩阵 A 可逆(invertible)或者矩阵 A 非奇异(nonsingular)。 反之,如果 A 为奇异(singular),则其没有逆矩阵。它的行列式为 0。另一个等价的说法是,A 为奇异阵,则方程 Ax=0 存在非零解 x。
5.高斯-若尔当消元法
高斯-约旦消元法是常用的求逆矩阵的方法,具体是在用高斯消元法的到上三角矩阵之后,按照若尔当的做法继续消元,用第一行
减去第二行的若干倍,最后原矩阵变为单位阵,这时右侧的矩阵即为逆矩阵。
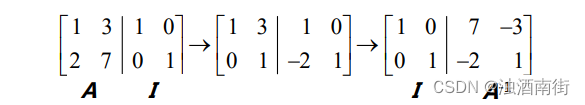
6.矩阵的 LU 分解
LU分解是一种矩阵分解方法,它将一个矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积,即A=LU。其中,L是一个下三角矩阵,U是一个上三角矩阵。LU分解可以用于解决线性方程组和矩阵求逆等问题。
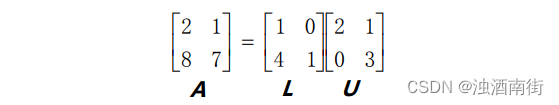
其中 U 为上三角阵(Upper triangular matrix),主元依次排列于它的对角线上,L 为下三角阵(Lower triangular matrix)。
7.三角矩阵
三角矩阵是指在矩阵中,一个方向上(通常是对角线以下或对角线以上)的元素全部为0的矩阵。根据对角线的位置,三角矩阵可以分为上三角矩阵和下三角矩阵两种类型。
下三角矩阵是指矩阵中对角线及其以上的元素全部为非零数,而对角线以下的元素全部为0的矩阵。 如: [ 1 0 0 a 2 0 b c 3 ] 如:\begin{bmatrix} 1&0&0\\a&2&0\\b&c&3 \end{bmatrix} 如: 1ab02c003
上三角矩阵是指矩阵中对角线及其以下的元素全部为非零数,而对角线以上的元素全部为0的矩阵。 如: [ 1 a b 0 2 c 0 0 3 ] 如:\begin{bmatrix} 1&a&b\\0&2&c\\0&0&3 \end{bmatrix} 如: 100a20bc3
三角矩阵通常是指方阵中的上三角矩阵和下三角矩阵,因此三角矩阵通常是方阵,尽管三角矩阵通常是方阵,但也存在非方阵的三角矩阵,例如下三角矩阵形如: [ 1 0 0 0 a 2 0 0 b c 3 0 ] \begin{bmatrix} 1&0&0&0\\a&2&0&0\\b&c&3&0 \end{bmatrix} 1ab02c003000
8.正定矩阵
若矩阵 A 满足对任意向量 x≠0 均有
x
T
A
x
x^TAx
xTAx>0,则称矩阵为正定矩阵,可以通过特征值、主元和行列式的办法来判断矩阵的正定性。
正定矩阵 A 是对称矩阵,它的逆矩阵
A
−
1
A^{-1}
A−1也是正定矩阵,逆矩阵的特征值是原矩阵的倒数,因此也都是正数。
给定一个 2 x 2 矩阵,有四个途径判定矩阵是否正定矩阵:
1) 特征值:
λ
1
>
0
,
λ
2
>
0
λ_1>0,λ_2>0
λ1>0,λ2>0
2) 行列式(所有子行列式):
a
>
0
,
a
c
−
b
2
>
0
a>0,ac-b^2>0
a>0,ac−b2>0
3) 主元:
a
>
0
,
(
a
c
−
b
2
)
/
a
>
0
a>0,(ac-b2)/a>0
a>0,(ac−b2)/a>0
4) 表达式
x
T
A
x
>
0
x^TAx>0
xTAx>0(x=0 除外)。通常这就是正定的定义,而前三条是用来验证正定性的条件。
如 A = [ 2 6 6 20 ] 如A=\begin{bmatrix} 2&6\\6&20 \end{bmatrix} 如A=[26620] ,就是一个正定矩阵;
持续更进中!!!!