数据结构与算法教程，数据结构C语言版教程！（第六部分、数据结构树，树存储结构详解）四

news2024/11/18 17:41:24

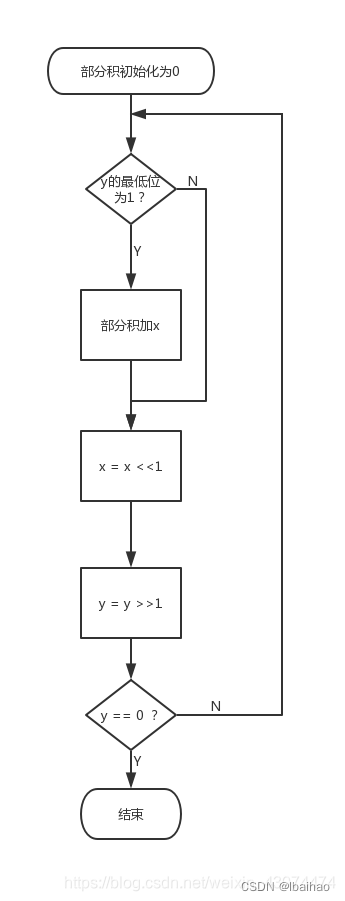
第六部分、数据结构树，树存储结构详解

数据结构的树存储结构，常用于存储逻辑关系为 "一对多" 的数据。

树存储结构中，最常用的还是二叉树，本章就二叉树的存储结构、二叉树的前序、中序、后序以及层次遍历、线索二叉树、哈夫曼树等，详细介绍二叉树。

树是数据结构中的重点，同时更是难点，没有捷径，需要初学者静下心，死扣各个知识点。

七、二叉树中序遍历（递归和非递归）算法C语言实现

二叉树中序遍历的实现思想是：

  1. 访问当前节点的左子树；
  2. 访问根节点；
  3. 访问当前节点的右子树；

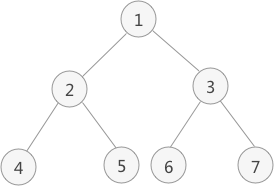
图 1 二叉树

以图  1 为例，采用中序遍历的思想遍历该二叉树的过程为：

  1. 访问该二叉树的根节点，找到 1；
  2. 遍历节点 1 的左子树，找到节点 2；
  3. 遍历节点 2 的左子树，找到节点 4；
  4. 由于节点 4 无左孩子，因此找到节点 4，并遍历节点 4 的右子树；
  5. 由于节点 4 无右子树，因此节点 2 的左子树遍历完成，访问节点 2；
  6. 遍历节点 2 的右子树，找到节点 5；
  7. 由于节点 5 无左子树，因此访问节点 5 ，又因为节点 5 没有右子树，因此节点 1 的左子树遍历完成，访问节点 1 ，并遍历节点 1 的右子树，找到节点 3；
  8. 遍历节点 3 的左子树，找到节点 6；
  9. 由于节点 6 无左子树，因此访问节点 6，又因为该节点无右子树，因此节点 3 的左子树遍历完成，开始访问节点 3 ，并遍历节点 3 的右子树，找到节点 7；
  10. 由于节点 7 无左子树，因此访问节点 7，又因为该节点无右子树，因此节点 1 的右子树遍历完成，即整棵树遍历完成；

因此，图 1 中二叉树采用中序遍历得到的序列为：

4 2 5 1 6 3 7

1、递归实现

二叉树的中序遍历采用的是递归的思想，因此可以递归实现，其 C 语言实现代码为：

#include <stdio.h>

#include <string.h>

#define TElemType int

//构造结点的结构体

typedef struct BiTNode{

        TElemType data;//数据域

        struct BiTNode *lchild,*rchild;//左右孩子指针

}BiTNode,*BiTree;

//初始化树的函数

void CreateBiTree(BiTree *T){

        *T=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->data=1;

        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->data=2;

        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild->data=5;

        (*T)->lchild->rchild->lchild=NULL;

        (*T)->lchild->rchild->rchild=NULL;

        (*T)->rchild->data=3;

        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->lchild->data=6;

        (*T)->rchild->lchild->lchild=NULL;

        (*T)->rchild->lchild->rchild=NULL;

        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->rchild->data=7;

        (*T)->rchild->rchild->lchild=NULL;

        (*T)->rchild->rchild->rchild=NULL;

        (*T)->lchild->lchild->data=4;

        (*T)->lchild->lchild->lchild=NULL;

        (*T)->lchild->lchild->rchild=NULL;

}

//模拟操作结点元素的函数，输出结点本身的数值

void displayElem(BiTNode* elem){

        printf("%d ",elem->data);

}

//中序遍历

void INOrderTraverse(BiTree T){

        if (T) {

                INOrderTraverse(T->lchild);//遍历左孩子

                displayElem(T);//调用操作结点数据的函数方法

                INOrderTraverse(T->rchild);//遍历右孩子

        }

        //如果结点为空，返回上一层

        return;

}

int main() {

        BiTree Tree;

        CreateBiTree(&Tree);

        printf("中序遍历算法: \n");

        INOrderTraverse(Tree);

}

运行结果：

中序遍历算法:
4 2 5 1 6 3 7

2、非递归实现

而递归的底层实现依靠的是栈存储结构，因此，二叉树的先序遍历既可以直接采用递归思想实现，也可以使用栈的存储结构模拟递归的思想实现。

中序遍历的非递归方式实现思想是：从根结点开始，遍历左孩子同时压栈，当遍历结束，说明当前遍历的结点没有左孩子，从栈中取出来调用操作函数，然后访问该结点的右孩子，继续以上重复性的操作。

除此之外，还有另一种实现思想：中序遍历过程中，只需将每个结点的左子树压栈即可，右子树不需要压栈。当结点的左子树遍历完成后，只需要以栈顶结点的右孩子为根结点，继续循环遍历即可。

两种非递归方法实现二叉树中序遍历的代码实现为：

#include <stdio.h>

#include <string.h>

#define TElemType int

int top=-1;//top变量时刻表示栈顶元素所在位置

//构造结点的结构体

typedef struct BiTNode{

        TElemType data;//数据域

        struct BiTNode *lchild,*rchild;//左右孩子指针

}BiTNode,*BiTree;

//初始化树的函数

void CreateBiTree(BiTree *T){

        *T=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->data=1;

        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->data=2;

        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild->data=5;

        (*T)->lchild->rchild->lchild=NULL;

        (*T)->lchild->rchild->rchild=NULL;

        (*T)->rchild->data=3;

        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->lchild->data=6;

        (*T)->rchild->lchild->lchild=NULL;

        (*T)->rchild->lchild->rchild=NULL;

        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->rchild->data=7;

        (*T)->rchild->rchild->lchild=NULL;

        (*T)->rchild->rchild->rchild=NULL;

        (*T)->lchild->lchild->data=4;

        (*T)->lchild->lchild->lchild=NULL;

        (*T)->lchild->lchild->rchild=NULL;

}

//前序和中序遍历使用的进栈函数

void push(BiTNode** a,BiTNode* elem){

        a[++top]=elem;

}

//弹栈函数

void pop( ){

        if (top==-1) {

                return ;

        }

        top--;

}

//模拟操作结点元素的函数，输出结点本身的数值

void displayElem(BiTNode* elem){

        printf("%d ",elem->data);

}

//拿到栈顶元素

BiTNode* getTop(BiTNode**a){

        return a[top];

}

//中序遍历非递归算法

void InOrderTraverse1(BiTree Tree){

        BiTNode* a[20];//定义一个顺序栈

        BiTNode * p;//临时指针

        push(a, Tree);//根结点进栈

        while (top!=-1) {//top!=-1说明栈内不为空，程序继续运行

                while ((p=getTop(a)) &&p){//取栈顶元素，且不能为NULL

                        push(a, p->lchild);//将该结点的左孩子进栈，如果没有左孩子，NULL进栈

                }

                pop();//跳出循环，栈顶元素肯定为NULL，将NULL弹栈

                if (top!=-1) {

                        p=getTop(a);//取栈顶元素

                        pop();//栈顶元素弹栈

                        displayElem(p);

                        push(a, p->rchild);//将p指向的结点的右孩子进栈

                }

        }

}

//中序遍历实现的另一种方法

void InOrderTraverse2(BiTree Tree){

        BiTNode* a[20];//定义一个顺序栈

        BiTNode * p;//临时指针

        p=Tree;

        //当p为NULL或者栈为空时，表明树遍历完成

        while (p || top!=-1) {

                //如果p不为NULL，将其压栈并遍历其左子树

                if (p) {

                        push(a, p);

                        p=p->lchild;

                }

                //如果p==NULL，表明左子树遍历完成，需要遍历上一层结点的右子树

                else{

                        p=getTop(a);

                        pop();

                        displayElem(p);

                        p=p->rchild;

                }

        }

}

int main(){

        BiTree Tree;

        CreateBiTree(&Tree);

        printf("中序遍历算法1: \n");

        InOrderTraverse1(Tree);

        printf("\n中序遍历算法2: \n");

        InOrderTraverse2(Tree);

}

运行结果

中序遍历算法1:
4 2 5 1 6 3 7
中序遍历算法2:
4 2 5 1 6 3 7

八、二叉树后序遍历（递归与非递归）算法C语言实现

二叉树后序遍历的实现思想是：从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素。

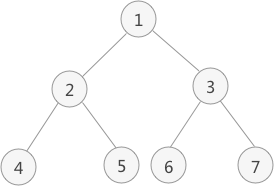
图 1 二叉树

如图 1 中，对此二叉树进行后序遍历的操作过程为：

  • 从根节点 1 开始，遍历该节点的左子树（以节点 2 为根节点）；
  • 遍历节点 2 的左子树（以节点 4 为根节点）；
  • 由于节点 4 既没有左子树，也没有右子树，此时访问该节点中的元素 4，并回退到节点 2 ，遍历节点 2 的右子树（以 5 为根节点）；
  • 由于节点 5 无左右子树，因此可以访问节点 5 ，并且此时节点 2 的左右子树也遍历完成，因此也可以访问节点 2；
  • 此时回退到节点 1 ，开始遍历节点 1 的右子树（以节点 3 为根节点）；
  • 遍历节点 3 的左子树（以节点 6 为根节点）；
  • 由于节点 6 无左右子树，因此访问节点 6，并回退到节点 3，开始遍历节点 3 的右子树（以节点 7 为根节点）；
  • 由于节点 7 无左右子树，因此访问节点 7，并且节点 3 的左右子树也遍历完成，可以访问节点 3；节点 1 的左右子树也遍历完成，可以访问节点 1；
  • 到此，整棵树的遍历结束。

由此，对图 1 中二叉树进行后序遍历的结果为：

4 5 2 6 7 3 1

1、递归实现

后序遍历的递归实现代码为：

#include <stdio.h>

#include <string.h>

#define TElemType int

//构造结点的结构体

typedef struct BiTNode{

        TElemType data;//数据域

        struct BiTNode *lchild,*rchild;//左右孩子指针

}BiTNode,*BiTree;

//初始化树的函数

void CreateBiTree(BiTree *T){

        *T=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->data=1;

        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->data=2;

        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild->data=5;

        (*T)->lchild->rchild->lchild=NULL;

        (*T)->lchild->rchild->rchild=NULL;

        (*T)->rchild->data=3;

        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->lchild->data=6;

        (*T)->rchild->lchild->lchild=NULL;

        (*T)->rchild->lchild->rchild=NULL;

        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->rchild->data=7;

        (*T)->rchild->rchild->lchild=NULL;

        (*T)->rchild->rchild->rchild=NULL;

        (*T)->lchild->lchild->data=4;

        (*T)->lchild->lchild->lchild=NULL;

        (*T)->lchild->lchild->rchild=NULL;

}

//模拟操作结点元素的函数，输出结点本身的数值

void displayElem(BiTNode* elem){

        printf("%d ",elem->data);

}

//后序遍历

void PostOrderTraverse(BiTree T){

        if (T) {

                PostOrderTraverse(T->lchild);//遍历左孩子

                PostOrderTraverse(T->rchild);//遍历右孩子

                displayElem(T);//调用操作结点数据的函数方法

        }

        //如果结点为空，返回上一层

        return;

}

int main() {

        BiTree Tree;

        CreateBiTree(&Tree);

        printf("后序遍历: \n");

        PostOrderTraverse(Tree);

}

运行结果：

后序遍历:
4 5 2 6 7 3 1

2、非递归实现

递归算法底层的实现使用的是栈存储结构，所以可以直接使用栈写出相应的非递归算法。

后序遍历是在遍历完当前结点的左右孩子之后，才调用操作函数，所以需要在操作结点进栈时，为每个结点配备一个标志位。当遍历该结点的左孩子时，设置当前结点的标志位为 0，进栈；当要遍历该结点的右孩子时，设置当前结点的标志位为 1，进栈。

这样，当遍历完成，该结点弹栈时，查看该结点的标志位的值：如果是 0，表示该结点的右孩子还没有遍历；反之如果是 1，说明该结点的左右孩子都遍历完成，可以调用操作函数。

完整实现代码为：

#include <stdio.h>

#include <string.h>

#define TElemType int

int top=-1;//top变量时刻表示栈顶元素所在位置

//构造结点的结构体

typedef struct BiTNode{

TElemType data;//数据域

struct BiTNode *lchild,*rchild;//左右孩子指针

}BiTNode,*BiTree;

//初始化树的函数

void CreateBiTree(BiTree *T){

        *T=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->data=1;

        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->data=2;

        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->rchild->data=5;

        (*T)->lchild->rchild->lchild=NULL;

        (*T)->lchild->rchild->rchild=NULL;

        (*T)->rchild->data=3;

        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->lchild->data=6;

        (*T)->rchild->lchild->lchild=NULL;

        (*T)->rchild->lchild->rchild=NULL;

        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->rchild->rchild->data=7;

        (*T)->rchild->rchild->lchild=NULL;

        (*T)->rchild->rchild->rchild=NULL;

        (*T)->lchild->lchild->data=4;

        (*T)->lchild->lchild->lchild=NULL;

        (*T)->lchild->lchild->rchild=NULL;

}

//弹栈函数 void pop( ){

        if (top==-1) {

                return ;

        }

        top--;

}

//模拟操作结点元素的函数，输出结点本身的数值

void displayElem(BiTNode* elem){

        printf("%d ",elem->data);

}

//后序遍历非递归算法

typedef struct SNode{

        BiTree p;

        int tag;

}SNode;

//后序遍历使用的进栈函数

void postpush(SNode *a,SNode sdata){

        a[++top]=sdata;

}

//后序遍历函数

void PostOrderTraverse(BiTree Tree){

        SNode a[20];//定义一个顺序栈

        BiTNode * p;//临时指针

        int tag;

        SNode sdata;

        p=Tree;

        while (p||top!=-1) {

                while (p) {

                        //为该结点入栈做准备

                        sdata.p=p;

                        sdata.tag=0;//由于遍历是左孩子，设置标志位为0

                        postpush(a, sdata);//压栈

                        p=p->lchild;//以该结点为根结点，遍历左孩子

                }

                sdata=a[top];//取栈顶元素

                pop();//栈顶元素弹栈

                p=sdata.p;

                tag=sdata.tag;

                //如果tag==0，说明该结点还没有遍历它的右孩子

                if (tag==0) {

                        sdata.p=p;

                        sdata.tag=1;

                        postpush(a, sdata);//更改该结点的标志位，重新压栈

                        p=p->rchild;//以该结点的右孩子为根结点，重复循环

                }

                //如果取出来的栈顶元素的tag==1，说明此结点左右子树都遍历完了，可以调用操作函数了

                else{

                        displayElem(p);

                        p=NULL;

                }

        }

}

int main(){

        BiTree Tree;

        CreateBiTree(&Tree);

        printf("后序遍历: \n");

        PostOrderTraverse(Tree);

}

运行结果

后序遍历:
4 5 2 6 7 3 1

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1417657.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

第一节课，用户管理--后端初始化，项目调通。二次翻工

第一节课，用户管理--后端初始化，项目调通。二次翻工

一、代码下载 网址&#xff1a; 用户管理第一节课&#xff0c;阿里生成代码包-CSDN博客 二、项目步骤&#xff0c;参考从 网址&#xff1a; 一、第一节课&#xff0c;用户管理--后端初始化&#xff0c;项目调通-CSDN博客 从这里开始跟随 &#xff08;一&#xff09;、跟随…
阅读更多...
eclipse用gerrit提交失败

eclipse用gerrit提交失败

1.gerrit简介 Gerrit&#xff0c;一种免费、开放源代码的代码审查软件&#xff0c;使用网页界面。利用网页浏览器&#xff0c;同一个团队的软件程序员&#xff0c;可以相互审阅彼此修改后的程序代码&#xff0c;决定是否能够提交&#xff0c;退回或者继续修改。它使用Git作为底…
阅读更多...
精通Python第13篇—数据之光：Pyecharts旭日图的魔法舞台

精通Python第13篇—数据之光：Pyecharts旭日图的魔法舞台

文章目录 引言准备工作绘制基本旭日图调整颜色和样式添加交互功能定制标签和标签格式嵌套层级数据高级样式与自定义进阶主题&#xff1a;动态旭日图数据源扩展&#xff1a;外部JSON文件总结 引言 数据可视化在现代编程中扮演着重要的角色&#xff0c;而Pyecharts是Python中一个…
阅读更多...
【数据分析】Excel中使用VBA进行宏编程

【数据分析】Excel中使用VBA进行宏编程

目录 0 准备工作1 VBA简介1.1 Excel VBA应用程序的构成1.2 事件驱动1.3 宏1.3.1 创建宏1.3.2 宏安全 2 VBA基础2.1 注释2.2 数据类型2.2.1 基本数据类型2.2.2 枚举类型2.2.3 用户自定义数据类型 2.2 变量2.3 常量2.4 运算符2.5 程序结构2.6 过程2.7 函数 3 Excel应用程序开发流…
阅读更多...
配置华为交换机环路检测案例

配置华为交换机环路检测案例

知识改变命运&#xff0c;技术就是要分享&#xff0c;有问题随时联系&#xff0c;免费答疑&#xff0c;欢迎联系&#xff01; 厦门微思网络​​​​​​https://www.xmws.cn 华为认证\华为HCIA-Datacom\华为HCIP-Datacom\华为HCIE-Datacom 思科认证\CCNA\CCNP\CCIE Linux\RHCE…
阅读更多...
给你一颗“定心丸”——记一次由线上事故引发的Log4j2日志异步打印优化分析

给你一颗“定心丸”——记一次由线上事故引发的Log4j2日志异步打印优化分析

一、内容提要 自知是人外有人&#xff0c;天外有天&#xff0c;相信对于Log4j2的异步日志打印早有老师或者同学已是熟稔于心&#xff0c;优化配置更是信手拈来&#xff0c;为了防止我在这里啰里八嗦的班门弄斧&#xff0c;我先将谜底在此公布&#xff1a;_log4j2.asyncQueueFu…
阅读更多...
【ArcGIS微课1000例】0098：查询河流流经过的格网

【ArcGIS微课1000例】0098：查询河流流经过的格网

本实验讲述，ArcGIS中查询河流流经过的格网，如黄河流经过的格网、县城、乡镇、省份等。 文章目录 一、加载数据二、空间查询三、结果导出四、注意事项一、加载数据 加载实验配套数据0098.rar中的河流（黄河）和格网数据，如下图所示： 接下来，将查询河流流经过的格网有哪些并…
阅读更多...
Python进阶(1) | 使用VScode写单元测试

Python进阶(1) | 使用VScode写单元测试

Python进阶(1) | 单元测试 2024.01.28 VSCode: 1.85.1 Linux(ubuntu 22.04) 文章目录 Python进阶(1) | 单元测试1. 目的2. Python Profile3. 单元测试框架3.1 什么是单元测试3.2 选一个单元测试框架3.3 编写 Python 单元测试代码3.4 在 VSCode 里发现单元测试3.5 再写一个单元…
阅读更多...
Linux的优先级说明

Linux的优先级说明

一、背景 在工作中&#xff0c;不少同学对nice&#xff0c;priority&#xff0c;schedue策略&#xff0c;实时优先级&#xff0c;普通进程优先级的概念混淆&#xff0c;导致最后的代码可能引入bug&#xff0c;本文将统一进行说明&#xff0c;部分内容参考网络大佬的文章 &…
阅读更多...
美化背景（拼图小游戏）

美化背景（拼图小游戏）

package Puzzlegame.com.wxj.ui;import javax.swing.*; import javax.swing.border.BevelBorder; import java.util.Random;public class GameJframe extends JFrame { //游戏主界面 //创建一个二维数组//目的&#xff1a;管理数据//加载图片的时候&#xff0c;会根据二维数组中…
阅读更多...
STM32读取MPU6050数据并通过角度值控制舵机运动（STM32、GY-521 MPU6050、SG90舵机、MG946舵机）

STM32读取MPU6050数据并通过角度值控制舵机运动（STM32、GY-521 MPU6050、SG90舵机、MG946舵机）

通过STM32F103C8T6读取MPU6050数据控制舵机运动&#xff08;STM32、GY-521 MPU6050、SG90舵机、MG946舵机&#xff09; 最终现象一、MPU6050数据读取二、舵机控制原理①什么是PWM&#xff1f;②STM32F103C8T6如何生成PWM&#xff1f;③控制舵机需要什么样的PWM波&#xff1f; 三…
阅读更多...
看图说话：Git图谱解读

看图说话：Git图谱解读

很多新加入公司的同学在使用Git各类客户端管理代码的过程中对于Git图谱解读不太理解&#xff0c;我们常用的Git客户端是SourceTree&#xff0c;配合P4Merge进行冲突解决基本可以满足日常工作大部分需要。不同的Git客户端工具对图谱展示会有些许差异&#xff0c;以下是SourceTre…
阅读更多...
jenkins对接K8S

jenkins对接K8S

创建连接K8S的凭据 查看需要使用到的命名空间 [rootk8s ~]# kubectl get ns |grep arts-system arts-system Active 16d创建service accounts [rootk8s ~]# kubectl create sa jenkins-k8s -n arts-system serviceaccount/jenkins-k8s created [rootk8s ~]# kubectl…
阅读更多...
使用vscode查bug

使用vscode查bug

具体操作 修改CMakeList.txt # set(CMAKE_BUILD_TYPE "Release")//注释Release模式 set(CMAKE_BUILD_TYPE "Debug")//设置为Debug模式 # set(CMAKE_CXX_FLAGS_RELEASE "-O3 -Wall -g")//注释*这行代码是用来设置 CMake 构建系统中 Release 模式…
阅读更多...
Go Zero微服务个人探究之路（十）实战走通微服务前台请求调用的一套流程model-＞rpc微服务-＞apiHTTP调用

Go Zero微服务个人探究之路（十）实战走通微服务前台请求调用的一套流程model-＞rpc微服务-＞apiHTTP调用

前言 Go语言凭借低占用&#xff0c;高并发等优秀特性成为后台编程语言的新星&#xff0c;GoZero框架由七牛云技术副总裁团队编写&#xff0c;目前已经成为Go微服务框架里star数量最多的框架 本文记录讲述笔者一步步走通前台向后台发出请求&#xff0c;后台api调用rpc服务的相…
阅读更多...
verilog编程之乘法器的实现

verilog编程之乘法器的实现

知识储备 首先来回顾一下乘法是如何在计算机中实现的。 假设现在有两个32位带符号定点整数x和y&#xff0c;我们现在要让x和y相乘&#xff0c;然后把乘积存放在z中&#xff0c;大家知道&#xff0c;两个32位数相乘&#xff0c;结果不会超过64位&#xff0c;因此z的长度应该为64…
阅读更多...
总结6（循环（for））

总结6（循环（for））

循环 定义&#xff1a; 某些代码会被重复执行 分类&#xff1a; for 1.格式 for(1; 2; 3) 语句A; 2.执行的流程&#xff08;1,2,A,3 2,A,3 2,A,3..........&#xff09; 单个for循环的使用 多个for循环的嵌套使用 1). for&#xff08;1; 2; 3&#xff09; for&#xff0…
阅读更多...
用通俗易懂的方式讲解：一种全新的大模型检索增强生成方法

用通俗易懂的方式讲解：一种全新的大模型检索增强生成方法

如何使大型语言模型更加事实、正确和可靠&#xff1f; 检索增强生成&#xff08;RAG&#xff09;是一种有效的方法&#xff0c;可以缓解大型语言模型的基本局限性&#xff0c;如幻觉和缺乏最新知识。 然而&#xff0c;如果您曾尝试过RAG&#xff0c;您会同意我所说的RAG易于原…
阅读更多...
【每日一题】4.LeetCode——环形链表

【每日一题】4.LeetCode——环形链表

&#x1f4da;博客主页&#xff1a;爱敲代码的小杨. ✨专栏&#xff1a;《Java SE语法》 ❤️感谢大家点赞&#x1f44d;&#x1f3fb;收藏⭐评论✍&#x1f3fb;&#xff0c;您的三连就是我持续更新的动力❤️ &#x1f64f;小杨水平有限&#xff0c;欢迎各位大佬指点&…
阅读更多...
RK3568平台开发系列讲解（Linux系统篇）互斥锁使用

RK3568平台开发系列讲解（Linux系统篇）互斥锁使用

🚀返回专栏总目录 文章目录 一、互斥锁API二、使用互斥锁的步骤三、互斥锁使用规则四、使用案例沉淀、分享、成长，让自己和他人都能有所收获！😄 一、互斥锁API 在Linux中，你可以使用互斥锁（Mutex）来实现多线程或多进程之间的互斥访问。互斥锁用于确保在同一时间只有一…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023