二刷代码随想录|Java版|回溯算法1|回溯基础理论+组合问题

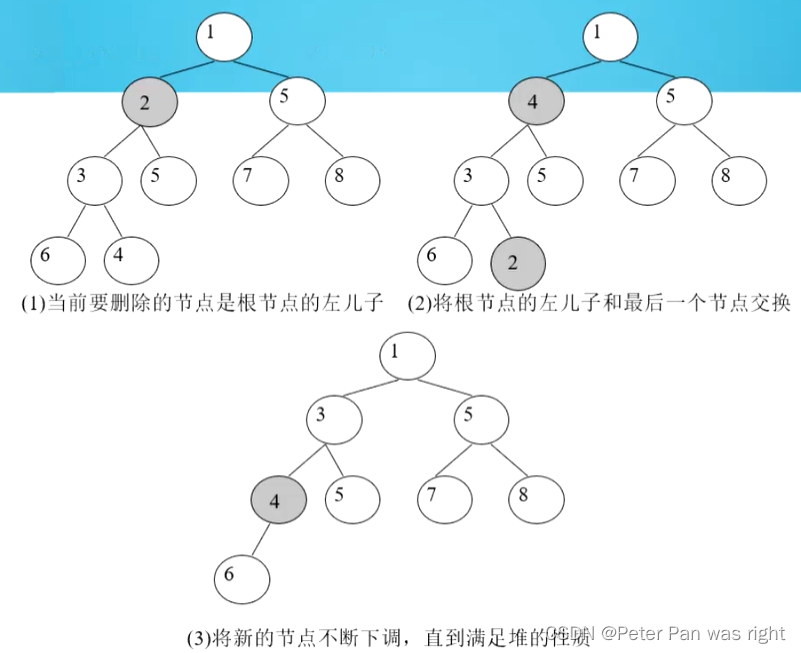
理论

写链表之类的真的很痛苦，赶紧跳到回溯！这次我想结合算法设计这本书，把java版写出来。放在第三部分吧。希望能够在研一完成这项工作！
从一刷总结以下的几个要点：

回溯方法模板性非常强！！可以解决绝大部分的问题。（代码随想录的模板非常够用啦）！
回溯树很重要，要画得出来！（集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。）以下是来自代码随想录的图！
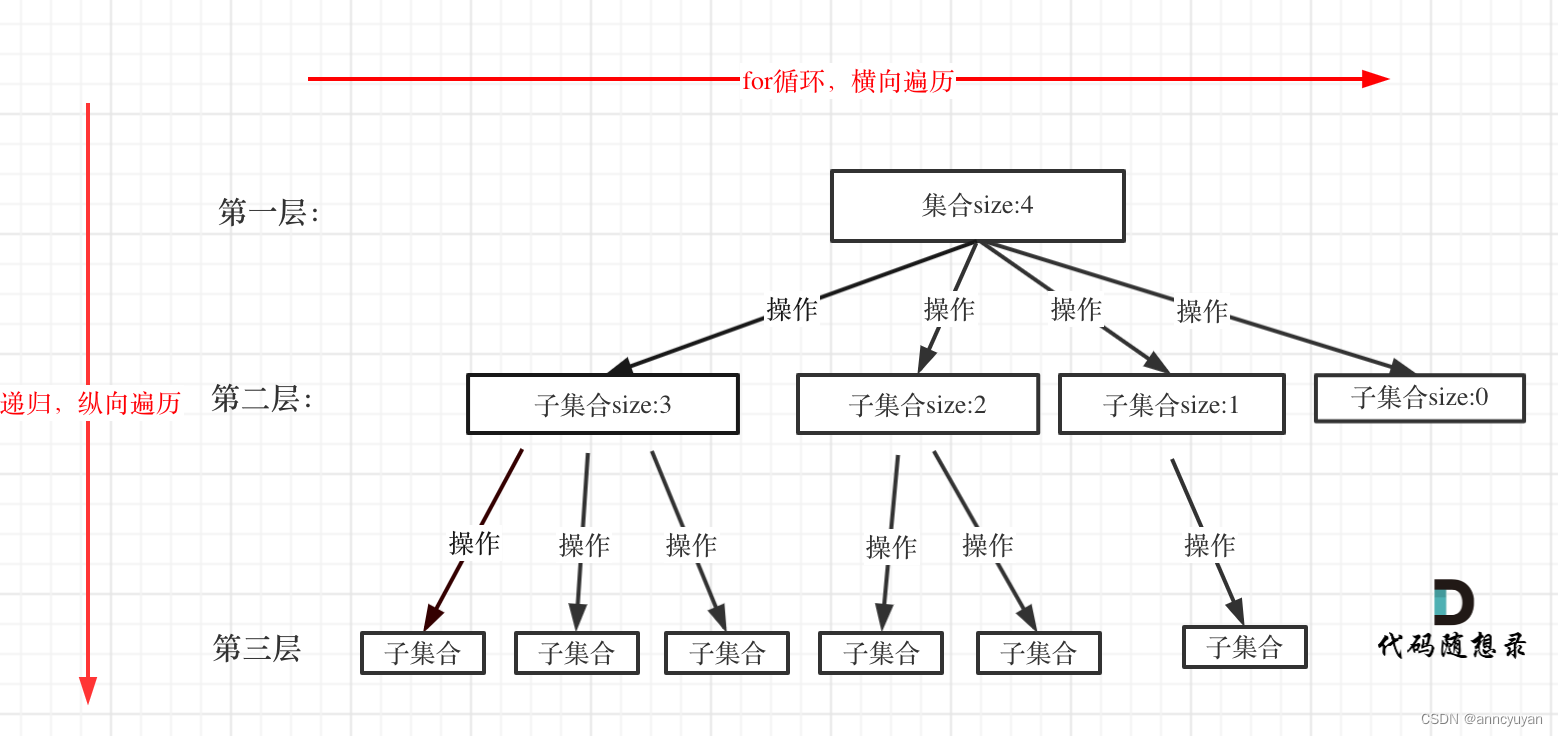
剪枝提高效率。
会涉及排序和组合（组合是不强调元素顺序的，排列是强调元素顺序。）。
会涉及到重复元素：层和树枝。

理论基础：设置递归函数实现穷举！
模版：常用的参数有（结束条件+解空间），startidx，used；全局的有path和res；函数内的有uset。

void Backtracing(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        Backtracing(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

1.1 组合：N个数里面按一定规则找出k个数的集合（要用used）

1.2 分割：一个字符串按一定规则有几种切割方式（回文，个数要求，子串？）

1.3 子集：一个N个数的集合里有多少符合条件的子集（组合的子问题）

1.4 排列：N个数按一定规则全排列，有几种排列方式

1.5 棋盘问题：N皇后，解数独等等

1.6 其他

习题

2.1 组合问题

用到的全局变量：这要求熟练掌握ArrayList和List的相关操作，add(元素)，remove(索引)，size()。

    List<Integer> path  = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

再次注意，组合问题要有startidx！
关于StringBuilder的操作

\\String：length(), charAt
\\数组String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
StringBuilder path = new StringBuilder();\\初始化
path.append(str.charAt(i));\\增加元素
path.deleteCharAt(path.length() - 1);\\删除元素
ans.add(path.toString());\\转换为String

2.1.1 77. 组合

题目要求在1-n内找到所有可能的k个数的组合。
需要记一下一下代码的时间复杂度，O(n*2^n)，目前还不知道怎么算。
代码随想录还给出了剪枝操作，讨论了n和k的关系，对于单次搜索的解空间大小，就是剩下的元素就算全部都枚举也不满足组合的个数要求要求，那么就结束。

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

class Solution {
    List<Integer> path  = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    public void Backtracing(int k, int startIdx, int n) {
        if(path.size()==k){
            ans.add(new ArrayList<>(path));//注意拷贝
            return;
        }
        //组合是无顺序的，需要startidx
        for(int i=startIdx; i<=n; i++){
            path.add(i);
            Backtracing(k, i+1, n);
            path.remove(path.size()-1);
        }
    }
    public List<List<Integer>> combine(int n, int k) {
        path.clear();
        ans.clear();
        Backtracing(k, 1, n);
        return ans;
    }
}

2.1.2 17. 电话号码的字母组合

这题主要就是2-9个按钮，每个按钮有固定的字母，求给定的一串数字，能打出的所有字母组合。
这样数的深度就是数字的长度，每层的解空间就是数字对应的按钮的字母。
难点在字符串的操作。
Java要用到StringBuilder，因为path如果是String的类无法更改字符。

class Solution {
    String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    StringBuilder path = new StringBuilder();
    List<String> ans = new ArrayList<>();
    public void BackTracing(int depth, String digits){
        if(depth==digits.length()){
            ans.add(path.toString());
            return;
        }
        String str = numString[digits.charAt(depth)-'0'];
        int width = str.length();
        for(int i=0; i<width; i++){
            path.append(str.charAt(i));
            BackTracing(depth+1, digits);
            path.deleteCharAt(path.length() - 1);
        }
    }
    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return ans;
        }
        BackTracing(0, digits);
        return ans;     
    }
}

2.1.3 216. 组合总和 III

这题的题目要求是1-9个数字，要求枚举的组合满足：和为n，个数为k，无重复元素。（一般来说，要求越多越好剪枝，和就是一个天然的剪枝条件。）
增加全局变量sum。当然也可以作为一个函数参数。

class Solution {
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    List<Integer> path  = new ArrayList<Integer>();
    int sum=0;
    public void Backtracing(int k, int startIdx, int n) {
        if(path.size()==k&&sum==n){
            ans.add(new ArrayList<>(path));//注意拷贝
            return;
        }
        //组合是无顺序的，需要startidx
        for(int i=startIdx; i <= 9 - (k - path.size()) + 1; i++){
            if(sum+i>n){
                return;
            }
            path.add(i);
            sum += i;
            Backtracing(k, i+1, n);
            path.remove(path.size()-1);
            sum -= i;
        }
        
    }
    public List<List<Integer>> combinationSum3(int k, int n) {
        path.clear();
        ans.clear();
        Backtracing(k, 1, n);
        return ans;
    }
}

2.1.4 39. 组合总和

本题要求给的candidates，找到和为target的组合，candidates 中的同一个数字可以无限制重复被选取。
深度由target控制（剪枝也是，排序，剪枝），宽度是candidate的元素个数。所以我认为不用startIdx了。
但出现这种情况：

其实是要的，startIdx保证重复选取当前元素，而不重复选取之前的元素，从而避免上述问题。

// 来自代码随想录
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates); // 先进行排序
        backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
        return res;
    }

    public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {
        // 找到了数字和为 target 的组合
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = idx; i < candidates.length; i++) {
            // 如果 sum + candidates[i] > target 就终止遍历
            if (sum + candidates[i] > target) break;
            path.add(candidates[i]);
            backtracking(res, path, candidates, target, sum + candidates[i], i);
            path.remove(path.size() - 1); // 回溯，移除路径 path 最后一个元素
        }
    }
}