给定 2n
个整数 a1,a2,…,an
和 m1,m2,…,mn
，求一个最小的非负整数 x
，满足 ∀i∈[1,n],x≡mi(mod ai)
。

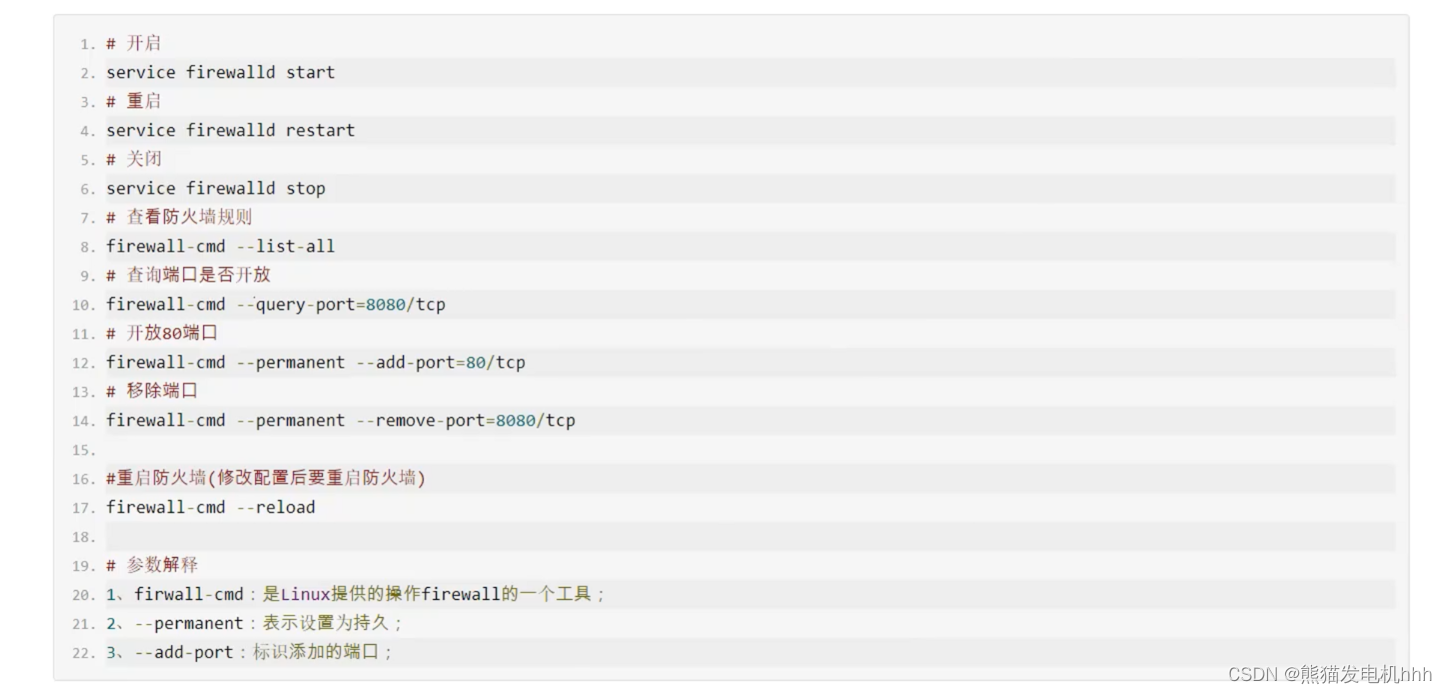
输入格式
第 1
行包含整数 n
。

第 2…n+1
行：每 i+1
行包含两个整数 ai
和 mi
，数之间用空格隔开。

输出格式
输出最小非负整数 x
，如果 x
不存在，则输出 −1
。

数据范围
1≤ai≤231−1
,
0≤mi<ai

1≤n≤25

所有 mi
的最小公倍数在 64
位有符号整数范围内。

输入样例：
2
8 7
11 9
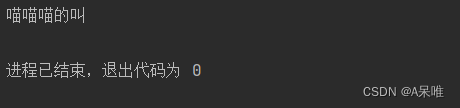
输出样例：
31

#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
int n;

LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main ()
{
    cin >> n;
    bool flag = true;
    LL a1, m1;
    cin >> a1 >> m1;
    for(int i = 0; i < n - 1; i ++ )
    {
        LL a2, m2;
        cin >> a2 >> m2;
        //先用扩展欧几里得求出k1和k2
        LL k1, k2;
        LL d = exgcd(a1, a2, k1, k2);
        if((m2 - m1) % d)
        {
            flag = false;
            break;
        }
        
        k1 *= (m2 - m1) / d;
        LL t = a2 / d;
        k1 = (k1 % t + t) % t;
        
        m1 = a1 * k1 + m1;
        a1 = abs(a1 / d * a2);
    }
    if(flag)
    {
        cout << (m1 % a1 + a1) % a1;
    }
    else
        cout << "-1" << endl;
    
    return 0;
}