原题链接:https://atcoder.jp/contests/abc338/tasks/abc338_d
Time Limit: 2 sec / Memory Limit: 1024 MB
Score: 425 points
问题陈述
AtCoder 群岛由 N 座岛屿组成,这些岛屿由 N 座桥梁连接。这些岛屿的编号从1到N,i(1≤i≤N−1)桥双向连接i和i+1岛,而N桥双向连接N和1岛。除了过桥之外,没有其他方式可以在岛屿之间旅行。
在这些岛屿上,经常会有从X1岛出发,依次游览X2,X3,…,XM岛的旅行团。游览过程中可能会经过正在游览的岛屿以外的其他岛屿,游览过程中经过桥梁的总次数定义为游览的长度*。
更确切地说,游是满足以下所有条件的l+1岛屿a0,a1,…,al序列,其长度定义为l:
- 对于所有j (0≤j≤l−1),岛屿aj和aj+1都由一座桥直接连接。
- 有一些 0=y1<y2<⋯<yM=l,对于所有 k (1≤k≤M),ayk=Xk。
由于财政困难,这些岛屿将关闭一座桥,以减少维护费用。求在最佳情况下选择关闭的桥时,可能的最小游程长度。
限制因素
- 3≤N≤2×1e5
- 2≤M≤2×1e5
- 1≤Xk≤N
- Xk
Xk+1 (1≤k≤M−1)
- 所有输入值均为整数。
输入输出描述
Sample Input 1Copy
3 3 1 3 2
Sample Output 1Copy
2
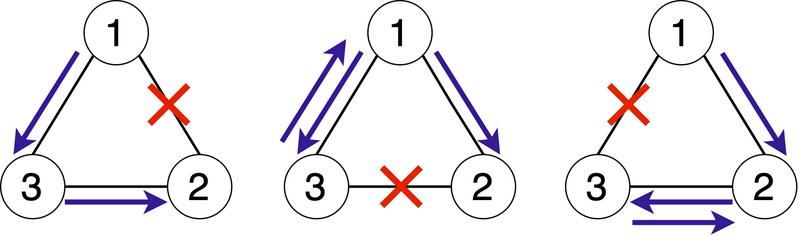
- 如果第一座桥关闭:以岛屿 (a0,a1,a2)=(1,3,2) 为序列,可以依次游览岛屿 1,3,2,可以进行长度为 2 的游览。没有更短的游程。
- 如果第二座桥关闭:根据岛屿(a0,a1,a2,a3)=(1,3,1,2)的顺序,可以依次游览岛屿1,3,2,可以进行长度为3的游览。没有更短的游程。
- 如果第三座桥关闭:按照岛屿(a0,a1,a2,a3)=(1,2,3,2)的顺序,可以依次游览岛屿1,3,2,可以进行长度为3的游览。没有更短的游程。
因此,在最佳选择关闭桥梁的情况下,可能的最小游程长度为 2。
下图从左到右分别显示了关闭桥梁 1,2,3 时的情况。带数字的圆圈代表岛屿,连接圆圈的线代表桥梁,蓝色箭头代表最短旅游路线。
Sample Input 2Copy
4 5 2 4 2 4 2
Sample Output 2Copy
8
同一岛屿可能在 X1,X2,…,XM 中出现多次。
Sample Input 3Copy
163054 10 62874 19143 77750 111403 29327 56303 6659 18896 64175 26369
Sample Output 3Copy
390009
解题思路:
先画个图来描述一下:
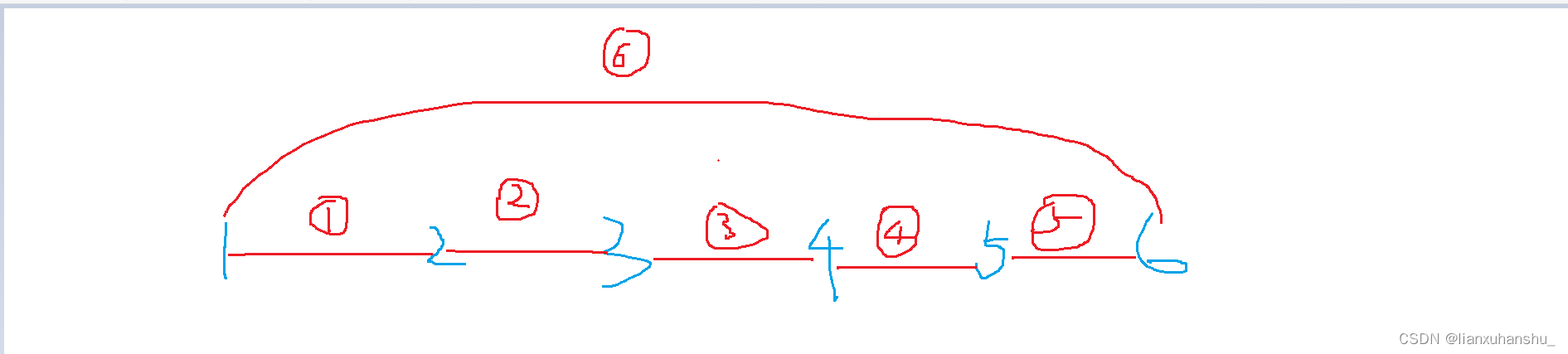
如上图所示例子,对于任意俩个a-b,从a到b和从b到a走过的路径一定是一样的,例如[2,4],从2走到4和从4走到2走的路径的长度一定是一样的,我们不妨让x=min(a,b],y=max(a,b),对于任意一条路径a<->b<->c<->d,任意俩个点可以看作一个区间,较小的那个数为左端点,较大的那个数为右端点,我们定义俩个vector数组l,r,r[i]存储右端点为i的所有区间的左端点,l[i]存储左端点为i的所有区间的右端点,然后枚举删每一条边, 然后看当前删除的边会对哪些区间的计算造成影响,首先考虑删除n号结点到1号结点之间的边,如上图所示就是删除6号边,那么此时任意区间的计算方式都是右端点减去左端点,此时计算这种删边方式走过的路径的长度,然后考虑删除i号点和i+1号点之间的i号边,然后考虑此时会对原来的区间造成哪些影响。
- 首先对于左端点位于i号结点的区间,那么这个区间的右端点肯定位于i号点右边,由于i号边被删除了,那么这个区间的贡献计算方式就不是右端点-左端点了,应该是先右端点走到n号点,n号点再走到1号点,然后1号点再走到左端点,所以把原来的右端点减去左端点的贡献减去,把新的贡献加上。
- 然后对于右端点位于i号结点的区间,那么这个区间的左端点肯定位于i号点左边,由于i号边被删除了,那么这个区间的计算方式就不是先右端点走到n号点,n号点在走到1号点,然后1号点再走到左端点了,而是直接从左端点走到右端点,所以把原来的右端点->n->1->左端点的贡献减去,加上新的贡献右端点-左端点。
这样枚举删每一条边了,根据造成的影响修改贡献,然后对于所有删边情况的总贡献求一个最小值即可。
时间复杂度:枚举删除每条边时间复杂度为O(n),然后每个区间只会被使用俩次,当遇到左端点的时候使用一次,遇到右端点的时候使用一次,时间复杂度为O(m),最终时间复杂度为O(n+m)。
空间复杂度:定义了俩个vector数组l,r,l[i]表示左端点为i的所有区间的右端点,r[i]表示右端点为i的所有区间的左端点,每个区间左端点右端点各存储一次,所以空间复杂度为O(n+m)。
cpp代码如下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10;
int n, m;
int a[N];
vector<int> r[N], l[N]; // l[i]表示左端点为i的所有区间的右端点,r[i]表示右端点为i的所有区间的左端点
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)
scanf("%d", &a[i]);
LL ans = 0;
for (int i = 2; i <= m; i++)
{
int x = a[i - 1], y = a[i];
if (x > y)
swap(x, y); // 让x表示左端点,y表示右端点
ans += y - x; // 开始删n号边,所有区间贡献的计算方式都是右端点-左端点
r[y].push_back(x); // 存储右端点是y的所有区间
l[x].push_back(y); // 存储左端点是x的所有区间
}
LL sum = ans;
for (int i = 1; i <= n; i++) // 枚举删每一条边
{
for (auto t : r[i])
{ // 对于右端点为i的所有区间根据删除的边修改贡献
sum += i - t;
sum -= (n - i + t);
}
for (auto t : l[i])
{ // 对于左端点为i的所有区间根据删除的边修改贡献
sum -= t - i;
sum += (n - t + i);
}
ans = min(ans, sum); // 更新答案
}
cout << ans << endl;
return 0;
}