-
通信原理第10页最后一段:
概率论告诉我们,事件的不确定程度可以用其出现的概率来描述。因此,消息中包含的信息量与消息发生的概率密切相关。消息出现的概率越小,则消息中包含的信息量就越大。 -
这句话怎么理解呢?
-
比如,一个方框代表一条消息,假设内部每个小球的出现概率相同
(1)第一个方框每种颜色的小球出现的概率是1/6,共有6个小球
(2)第二个方框每种颜色的小球出现的概率1/n(n→ ∞ \infty ∞),共有n个小球
即:概率越小,能包含的小球就越多,该结论仅解释概率与信息量的关系

-
通信原理第11页开头:
I I I(信息量)与 P ( x ) P(x) P(x)(消息发生概率)之间的关系应当反映如下规律:
(1)消息中所含的信息量是该消息出现的概率的函数,即
I = I [ P ( x ) ] I=I[P(x)] I=I[P(x)]
(2) P ( x ) P(x) P(x)越小, I I I越大;反之, I I I越小;且当 P ( x ) = 1 P(x)=1 P(x)=1时, I = 0 I=0 I=0; P ( x ) = 0 P(x)=0 P(x)=0时, I = ∞ I=\infty I=∞
(3)若干个互相独立事件构成的消息,所含信息量等于各独立事件信息量之和,也就是说,信息具有相加性,即
I [ P ( x 1 ) P ( x 2 ) ⋯ ] = I [ P ( x 1 ) ] + I [ P ( x 2 ) ] + ⋯ I[P(x_1)P(x_2)\cdots]=I[P(x_1)]+I[P(x_2)]+\cdots I[P(x1)P(x2)⋯]=I[P(x1)]+I[P(x2)]+⋯
不难看出,若 I I I与 P ( x ) P(x) P(x)之间的关系式为
I = log a 1 P ( x ) = − log a P ( x ) I = \log_a\frac{1}{P(x)}=-\log_aP(x) I=logaP(x)1=−logaP(x) -
满足上述三个条件的简单函数,仅 log \log log函数,以 y = log 2 a y=\log_2a y=log2a函数为例,假设 a = 1 P ( x ) a=\frac{1}{P(x)} a=P(x)1
当 P ( x ) P(x) P(x)概率增大, a a a就越小,y就越大
当 P ( x ) P(x) P(x)概率减小, a a a就越大,y就越小
当 P ( x ) = 1 P(x)=1 P(x)=1, a = 1 a=1 a=1,则 y = 0 y=0 y=0
当 P ( x ) → 0 P(x)→0 P(x)→0, a → ∞ a→\infty a→∞,则 y → ∞ y→\infty y→∞
符合上述三条规律

-
通信原理第11页中间:
通常广泛使用的单位为比特,这时有
I = log 2 1 P ( x ) = − log 2 P ( x ) ( b ) I=\log_2\frac{1}{P(x)}=-\log_2P(x)\qquad(b) I=log2P(x)1=−log2P(x)(b)
这个公式暂时先死记,二进制传输系统中度量信息量的公式就是这小子了
-为什么用比特, log \log log函数的底数就是2呢?最后解答 -
通信原理第11页【例1-1】:
这里就不贴原文了,以下内容,详细解释信息量是什么东西,个人觉得还是从多进制开始涉入才理解深刻 -
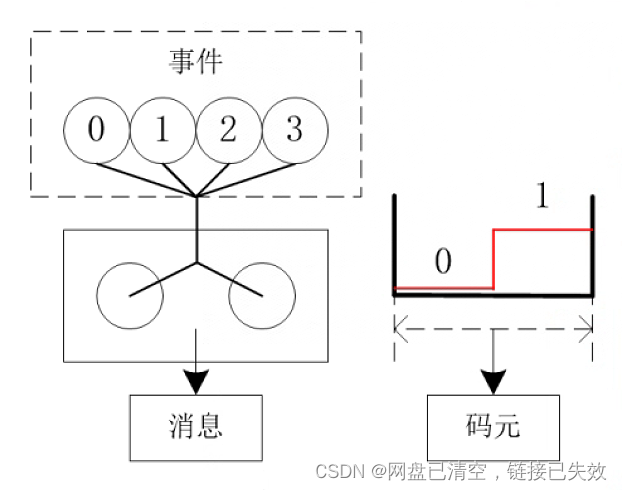
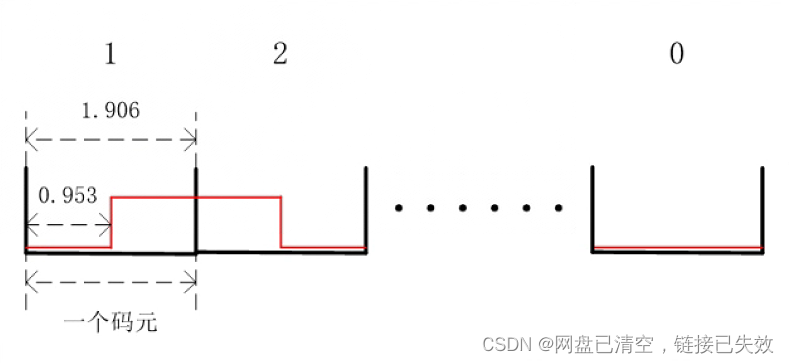
图中一个方框就代表一个码元,一条消息有n个码元,而这一个码元可能会发生4种事件,即4个值,二进制传输系统中,最小传输单元仅用高低电平表示0或1,这里方框内的圆圈就是最小传输单元,只能表示0或者1
那么一个码元需要表示4个值,就需要两个最小传输单元 -
视角转到电平信号,假设一条消息只有一个码元,而这一个码元需要表示为4个值,就需要两个bit,而这两个bit就是信息量,也就是一个码元内,需要多少个bit来表示出所有的值,而信息量的单元就是比特
-
再比如,一个码元需要表示0至7的整数,每个整数等概出现,就需要3bit来表示,那么它的信息量就是3bit
-
前面都是再以2的幂来举例的,这次来个非2的幂的数
比如说,一个码元需要表示0-9的整数,每个整数等概出现,即 P ( x ) = 1 10 P(x)=\frac{1}{10} P(x)=101,根据公式(1.4-2)得
I = − log 2 P ( x ) = − log 2 1 10 ≈ 3.321928 ( b i t ) I=-\log_2P(x)=-\log_2\frac{1}{10}\approx3.321928(bit) I=−log2P(x)=−log2101≈3.321928(bit)
也就是说一个码元需要约3.321928个bit才能表示0-9的整数 -
特别的,当一个码元仅需要表示两个数值0或1时,一个码元就只需要一个bit就可以表示2个数值了,这种情况下,一个码元就是一个bit,4进制一个码元有2bit,8进制一个码元有3bit,10进制一个码元约有3.321928个bit…
-
通信原理第12页开头:
-
上述是在每个事件等概出现的情况下,探讨的,下面来讨论各事件非等概的情况下,怎么计算信息量(一个码元需要多少个bit才能表示所有数值)
设离散信源是一个由 M M M个符号组成的集合,其中每个符号 x i ( i = 1 , 2 , 3 , . . . , M ) x_i(i=1,2,3,...,M) xi(i=1,2,3,...,M)按照一定的概率 P ( x i ) P(x_i) P(xi)独立出现,即
[ x 1 , x 2 , ⋯ , x M P ( x 1 ) , P ( x 2 ) , ⋯ , P ( x M ) ] , 且 ∑ i = 1 M P ( x i ) = 1 \begin{bmatrix} x_1, & x_2, &\cdots, & x_M \\ P(x_1), &P(x_2), &\cdots, & P(x_M) \end{bmatrix} ,且\sum_{i=1}^{M}P(x_i)=1 [x1,P(x1),x2,P(x2),⋯,⋯,xMP(xM)],且i=1∑MP(xi)=1
则 x 1 , x 2 , ⋯ , x M x_1,x_2,\cdots,x_M x1,x2,⋯,xM所包含的信息量分别为
− log 2 P ( x 1 ) , − log 2 P ( x 2 ) , ⋯ , − log 2 P ( x M ) -\log_2P(x_1),-\log_2P(x_2),\cdots,-\log_2P(x_M) −log2P(x1),−log2P(x2),⋯,−log2P(xM)
于是,每个符号所含信息量的统计平均值,即平均信息量为
H ( x ) = P ( x 1 ) [ − log 2 P ( x 1 ) ] + P ( x 2 ) [ − log 2 P ( x 2 ) ] + ⋯ + P ( x M ) [ − log 2 P ( x M ) ] = − ∑ i = 1 M P ( x i ) [ log 2 P ( x i ) ] \begin{aligned} H(x)&=P(x_1)[-\log_2P(x_1)]+P(x_2)[-\log_2P(x_2)]+\cdots+P(x_M)[-\log_2P(x_M)]\\ &=-\sum_{i=1}^MP(x_i)[\log_2P(x_i)] \end{aligned} H(x)=P(x1)[−log2P(x1)]+P(x2)[−log2P(x2)]+⋯+P(xM)[−log2P(xM)]=−i=1∑MP(xi)[log2P(xi)] -
这里先以等概举例,比如4进制,0-3的每个数值等概出现,即1/4,那么平均信息量就等于
H ( x ) = − ∑ i = 1 M P ( x i ) [ log 2 P ( x i ) ] = 1 4 ( − log 2 1 4 ) + 1 4 ( − log 2 1 4 ) + 1 4 ( − log 2 1 4 ) + 1 4 ( − log 2 1 4 ) = 2 ( b i t ) \begin{aligned} H(x)&=-\sum_{i=1}^MP(x_i)[\log_2P(x_i)]\\ &=\frac{1}{4}(-\log_2\frac{1}{4})+\frac{1}{4}(-\log_2\frac{1}{4})+\frac{1}{4}(-\log_2\frac{1}{4})+\frac{1}{4}(-\log_2\frac{1}{4})\\ &=2(bit) \end{aligned} H(x)=−i=1∑MP(xi)[log2P(xi)]=41(−log241)+41(−log241)+41(−log241)+41(−log241)=2(bit)
是不是跟上面等概求信息量的结果相同,这就对咯,当 P ( x i ) = 1 / M P(x_i)=1/M P(xi)=1/M(每个符号等概率独立出现)时,式(1.4-6)即成为式(1.4-4),此时信源的熵有最大值,而熵是描述体系混乱程度的度量 -
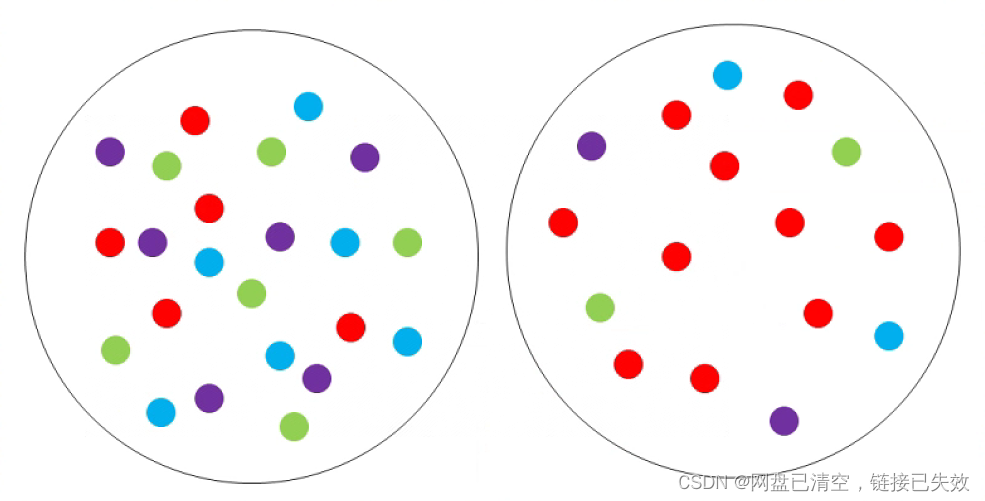
模拟4进制,共4种颜色
第一个圆,每个颜色等概出现,肉眼可见杂乱,此时熵最大
第二个圆,红色概率最大,其它的最低,肉眼可见整个体系趋向于红色,熵比较小
-
通信原理第12页【例1-2】:
一离散信源由0,1,2,3共4个符号组成,它们出现的概率分别为3/8,1/4,1/4,1/8,且每个符号的出现都是独立的。试求某条消息201020130213001203210100321010023102002010312032100120210的信息量
H ( x ) = − ∑ i = 1 M P ( x i ) [ log 2 P ( x i ) ] = 3 8 ( − log 2 3 8 ) + 1 4 ( − log 2 1 4 ) + 1 4 ( − log 2 1 4 ) + 1 8 ( − log 2 1 8 ) = 1.906 ( b i t ) \begin{aligned} H(x)&=-\sum_{i=1}^MP(x_i)[\log_2P(x_i)]\\ &=\frac{3}{8}(-\log_2\frac{3}{8})+\frac{1}{4}(-\log_2\frac{1}{4})+\frac{1}{4}(-\log_2\frac{1}{4})+\frac{1}{8}(-\log_2\frac{1}{8})\\ &=1.906(bit) \end{aligned} H(x)=−i=1∑MP(xi)[log2P(xi)]=83(−log283)+41(−log241)+41(−log241)+81(−log281)=1.906(bit)
-
即,一个码元只需要1.906个bit就能表示这4个符号,这条消息有57个码元,则总信息量为
I = 57 × 1.906 = 108.64 ( b i t ) I=57×1.906=108.64(bit) I=57×1.906=108.64(bit)
-
通信原理第13页中间:
对于数字通信系统,其频谱利用率定义在单位带宽(每赫)内的传输速率,即
η = R B B ( B a u d / H z ) \eta=\frac{R_B}{B}\qquad(Baud/Hz) η=BRB(Baud/Hz)
或
η b = R b B ( b / ( s ⋅ H z ) ) \eta_b=\frac{R_b}{B}\qquad(b/(s·Hz)) ηb=BRb(b/(s⋅Hz))
其中 R B R_B RB为码元传输速率,简称传码率。它被定义为单位时间(每秒)传输的码元的数目,单位为波特(Baud),因此,又称 R B R_B RB为波特率
设每个码元的长度为 T B ( s ) T_B(s) TB(s),则有
R B = 1 T B ( B a u d ) R_B=\frac{1}{T_B}\qquad(Baud) RB=TB1(Baud)
其中 R b R_b Rb为信息传输速率,简称传信率,又称比特率。它定义为单位时间内传输的平均信息量,单位为比特/秒(b/s) -
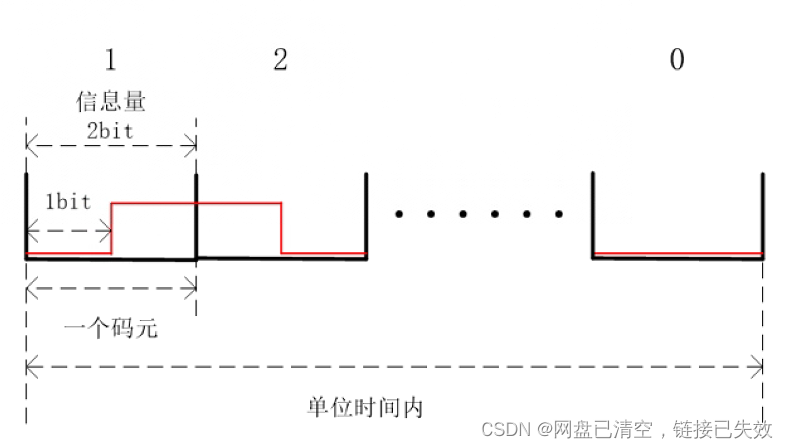
以4进制为例,单位时间内传输 m m m个码元,而一个码元有2bit信息量,那么单位时间传输 2 m 2m 2m个bit
特别的,2进制,此时波特率和比特率数值上相等
-
通信原理第13页末尾:
因为一个 M M M进制码元携带 log 2 M \log_2M log2M比特的信息量,所以码元速率和信息速率有以下确定的关系,即
R b = R B log 2 M ( b / s ) R_b=R_B\log_2M\qquad(b/s) Rb=RBlog2M(b/s)
其中 log 2 M \log_2M log2M只针对每个符号出现概率相同的情况下计算,因为概率相同的情况下,平均信息量就等于单个符号的信息量
若每个符号出现的概率不同,则 log 2 M \log_2M log2M需要替换成平均信息量来计算了,如下
R b = − R B ∑ i = 1 M P ( x i ) [ log 2 P ( x i ) ] R_b=-R_B\sum_{i=1}^MP(x_i)[\log_2P(x_i)] Rb=−RBi=1∑MP(xi)[log2P(xi)] -
回到中间那个问题:为什么比特, log \log log函数的底数就是2呢?
因为数字系统传输只能表示0或1,即一个信息只能表示2个状态或数值,则 log \log log函数的底数为2,信息量的单位为比特(bit)
若一个信息能表示 e e e个状态或数值,则 log \log log函数的底数为 e e e,信息量的单位为奈特(nat)
若一个信息能表示 10 10 10个状态或数值,则 log \log log函数的底数为 10 10 10,信息量的单位为哈特莱(Hartley)

它们的信息量都为1,但是单位不同 -
以哈特莱为例,共10个事件,每个事件等概出现,则 P ( x ) = 1 / 10 P(x)=1/10 P(x)=1/10,带入公式中
I = log 10 1 P ( x ) = log 10 1 1 / 10 = 1 ( H a r t l e y ) I=\log_{10}\frac{1}{P(x)}=\log_{10}\frac{1}{1/10}=1\qquad(Hartley) I=log10P(x)1=log101/101=1(Hartley)
也就是说一个码元内的信息量就是 1 哈特莱
一张图文深入了解信息量概念
news2026/2/15 16:36:17
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1416411.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
小红构造数组-牛客周赛 Round 29(DFS方法)
题目很直白,方法就是暴力即可。
虽然说数据范围显得很大,但是在长整型范围内,一个数字的素因子数量最多不超64,而如果是不相同的素因子,虽然没有计算过,但是如果是12个不同的素因子应该会超过数据范围了。…
消息中间件之八股面试回答篇:三、RabbitMQ如何解决消息堆积问题(100万条消息堆积)+RabbitMQ高可用性和强一致性机制+回答模板
RabbitMQ中的消息堆积问题
当生产者发送消息的速度超过了消费者处理消息的速度,就会导致队列中的消息堆积,直到队列存储消息达到上限。之后发送的消息就会成为死信,可能会被丢弃,这就是消息堆积问题。
解决消息堆积有三种种思路…
c++阶梯之引用与内联函数
1. 引用
1.1 引用概念 引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内存空间,它和它引用的变量共用同一块内存空间。 语法
类型& 引用变量名(对象名) 引用实体;
示例
很显然,在下面这…
21.Arrays类
Arrays类 1. 概述2. 常见方法3. sort 方法的自定义排序4. 代码示例5. 输出结果6. 注意事项 具体信息请查看 API 帮助文档 1. 概述
Arrays类是Java中的一个工具类,位于java.util包中。
它提供了一组静态方法,用于操作数组。通过Arrays类,我们…
springboot136人口老龄化社区服务与管理平台
简介 【毕设源码推荐 javaweb 项目】基于springbootvue 的 适用于计算机类毕业设计,课程设计参考与学习用途。仅供学习参考, 不得用于商业或者非法用途,否则,一切后果请用户自负。 看运行截图看 第五章 第四章
获取资料方式 **项…
web前端---------盒子模型2
一------内边距
padding 属性用来设置元素的内边距长度,元素在默认情况下没有内边距,其值为none。
(1)当 padding 属性中仅含一个值时,该长度应用在上、下、左、右四个区域。
(2)当 padding …
Java二分查找-图文
一、二分查找概念 二分查找也叫折半查找,是在一组有序(升序/降序)的数据中查找一个元素,它是一种效率较高的查找方。
二、二分查找原理 1.二分查找的数组必须是有序数值型数组。 2.将想要查找的目标元素与查找范围内的中间元素进行比较,如果…
文件包含漏洞长度截断
长度截断 文件漏洞的利用方式什么是长度截断通过实操理解00截断对版本要求更高一点,而长度截断则是利用了windows的系统漏洞,就是windows文件名(就是文件名后缀之后)之后如果有空格,或者是点都会被忽略掉,也…
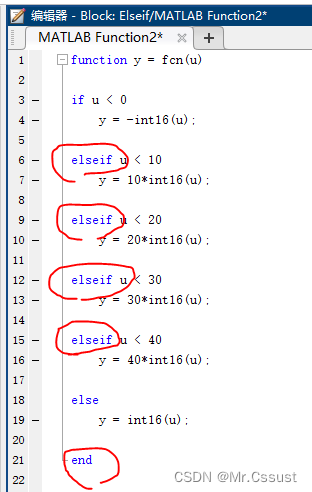
研发日记,Matlab/Simulink避坑指南(八)——else if分支结构Bug
文章目录
前言
背景介绍
问题描述
分析排查
解决方案
总结归纳 前言 见《研发日记,Matlab/Simulink避坑指南(三)——向上取整Bug》 见《研发日记,Matlab/Simulink避坑指南(四)——transpose()转置函数Bug》 见《研发日记,Matlab/Simuli…
Spring Cloud + Vue前后端分离-第13章 网站开发
源代码在GitHub - 629y/course: Spring Cloud Vue前后端分离-在线课程
Spring Cloud Vue前后端分离-第13章 网站开发
13-1 网站模块的搭建
新建web模板
1.网站开发,增加web模块,使用命令:vue create web
vue版本4.2.3
大家拿到一个v…
【Web】小白也能做的RWCTF体验赛baby题部分wp
遇到不会的题,怎么办!有的师傅告诉你完了,废了,寄了!只有Z3告诉你,稳辣!稳辣!都稳辣!
这种CVE复现的题型,不可能要求选手从0到1进行0day挖掘,其实…
如何快速上手一个vue框架
安装nvm
下载nvm-setup.zip: https://github.com/coreybutler/nvm-windows/releases 解压安装nvm: 创建两个文件夹,一个是nvm的安装位置,另一个是node.js的下载位置。不需要配置环境变量和修改setting文件了 检查nvm是否安装成功…
Redis客户端之Redisson(三)Redisson分布式锁
一、背景:
高效的分布式锁设计应该包含以下几个要点:
1、互斥:
在分布式高并发的条件下,我们最需要保证,同一时刻只能有一个线程获得锁,这是最基本的一点
2、防止死锁:
在分布式高并发的条…
【vue3源码】vue源码探索之旅:项目介绍
简言
记录下我眼中的vue源码项目。 gitHubvue3项目仓库
项目要求: vue版本 3.4.15nodeV18.12.0以上使用pnpm包管理器vitest测试框架Vue3
vue3是渐进式JavaScript框架,易学易用,性能出色,适用场景丰富的 Web 前端框架。 Vue 是一个框架,也是一个生态。其功能覆盖了大部分…
VBA技术资料MF111:将表对象转换为正常范围
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…
【Linux C | 进程】Linux 进程间通信的10种方式(1)
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…
python14-Python的字符串之原始字符串
由于字符串中的反斜线都有特殊的作用。
因此当字符串中包含反斜线时,就需要对其进行转义。
比如写一条Windows的路径:D:\pythonStudy\demo,如果在Python 程序中直接这样写肯定是不行的,需要写成:D:\\pythonStudy\\demo,这很烦人.
此时可借助于原始字符串来解决这个问题。…
LeNet跟LeNet5详解
1 LeNet结构 主要是为了手写数字识别
具体结构讲解:从图中例子可得
1 先传入一个灰度图像尺寸为1x28x28,通道数为1,尺寸为28x28的灰度图像
2 第一层5x5卷积,经过公式 输入图像尺寸-卷积核尺寸2padding/步长1,&#…
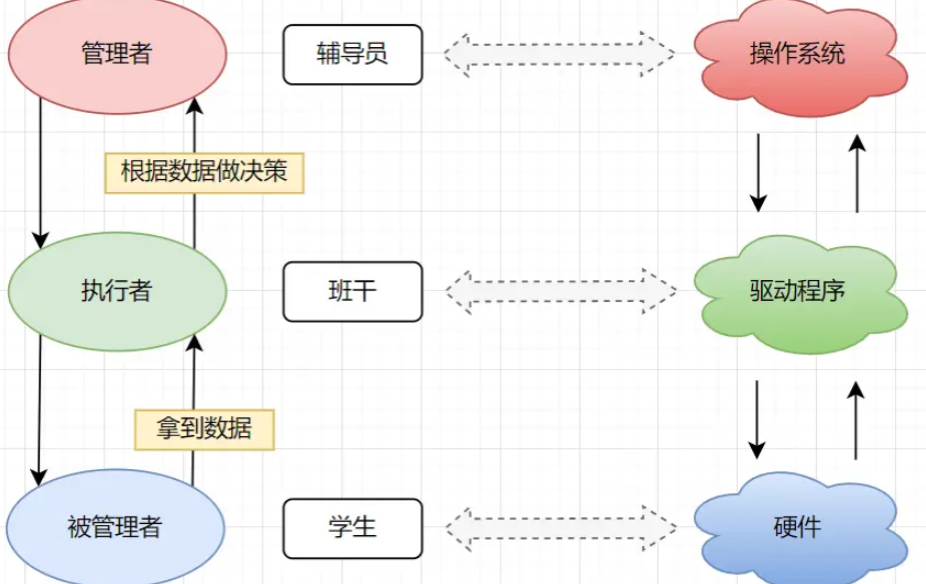
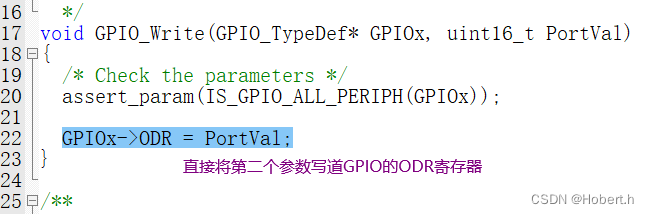
32GPIO输入LED闪烁蜂鸣器
一.GPIO简介 所有的GPIO都挂载到APB2上,每个GPIO有16个引脚
内核可以通过APB2对寄存器进行读写,寄存器都是32位的,但每个引脚端口只有16位
驱动器用于增加信号的驱动能力
二.具体…