一、前言
判断推理这一题型主要具体分为四种题型:
1.图形推理
2.类比推理
3.定义判断
4.逻辑判断
每种题型做题方法又不一样。
才本文采用总分的形式结构。
每一小标题的下面紧接着就是总结。
二、图形推理常见的命题形式
图形推理常见的命题形式:
1.组图规律
2.分组分类
3.空间重构
(1)组图规律
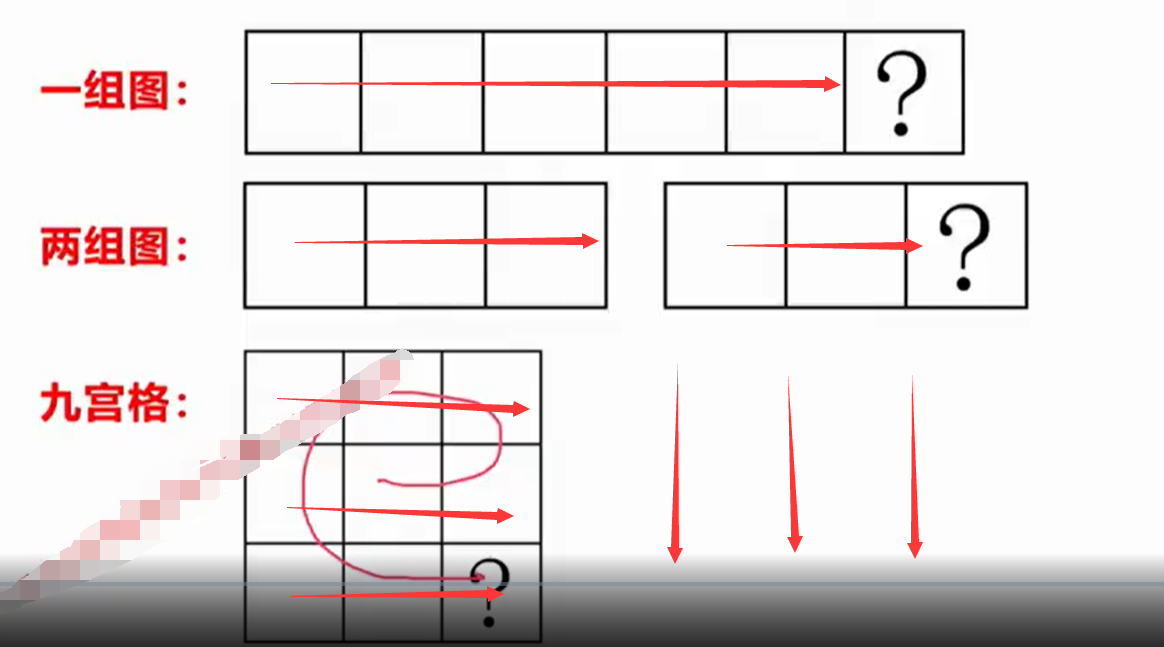
一组图的一般是从左往右找规律确定最后的图像。
两组图的一般是从左面一组中规律,在右面一组中应用规律。
九宫格的一般分为两种情况:
横着或者竖着为一组,然后第一组找规律,第二组验证规律,第三组应用规律。
当然也有些比较恶心的题会斜着或者z字型或者s型的,但是很少。
(2)分组分类
分组分类:每道题会给出6个图形,并且图形进行了编号,要求分为两组,每组各自具有共同的规律。
(3)空间重构
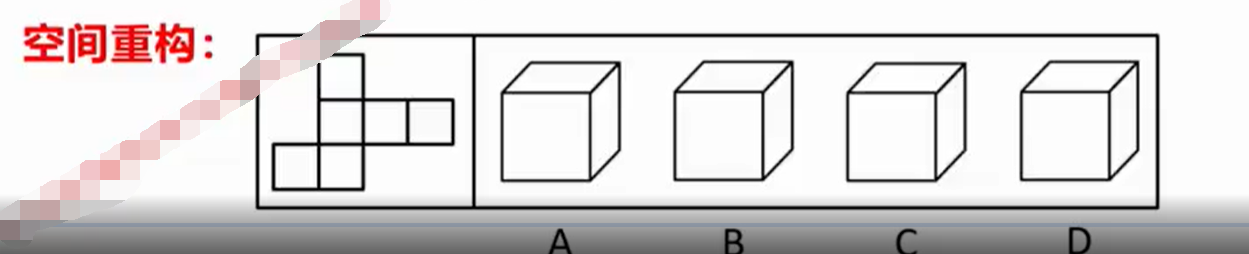
类似数学上立体几何的题。
比如,给出一个图形的展开图让你选出原图形,或者给出原图形让你选择展开图。
(4)空间类
比如:截面图,三视图,立体拼合,这些也可以看做空间重构的进阶。
三、图形推理常考规律
1.位置规律
2.样式规律
3.属性规律
4.特殊规律
5.数量规律
6.空间重构
如何快速的定位某道题的规律?——看图形特征
(1)位置规律
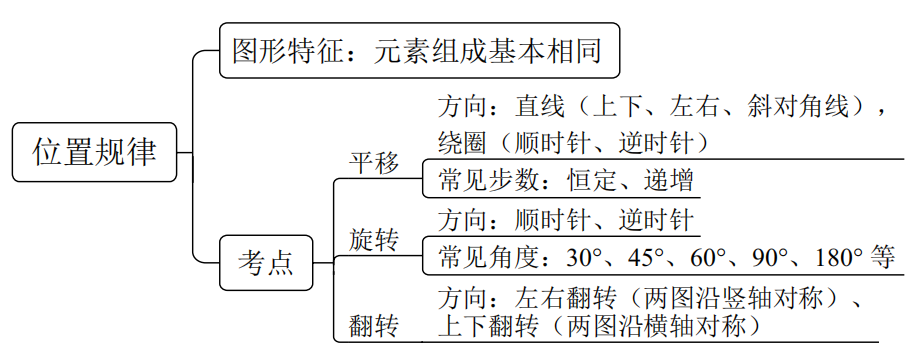
①平移

例题:
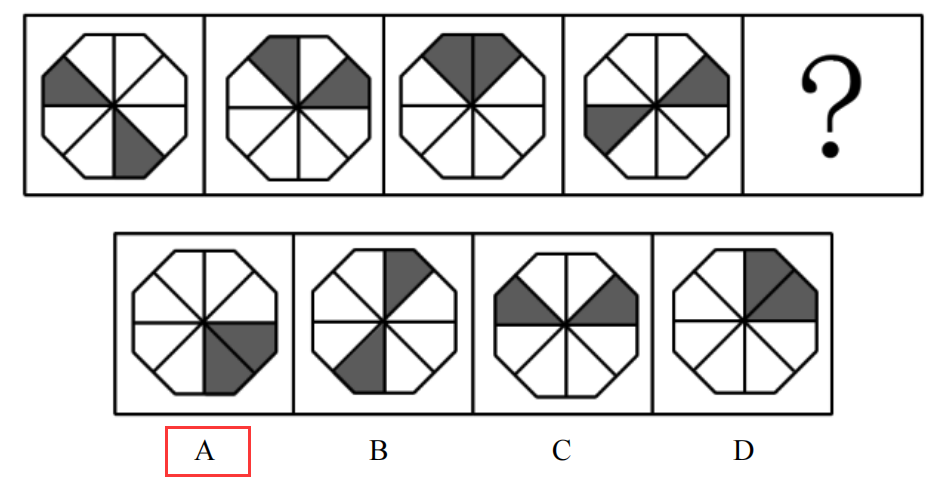
注意:
当多个相同元素平移时,我们就近假设。
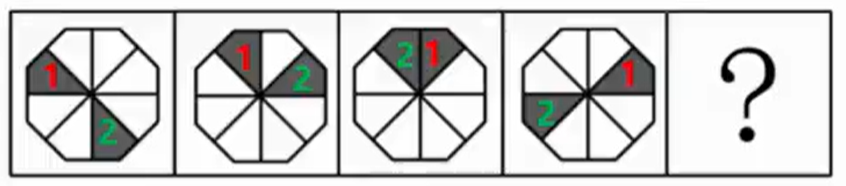
两个相同元素离得最近的视为一个元素。
可以标号方便平移
标号为1的图形顺时针每次平移一格,
标号为2的图形逆时针每次平移两格。
有朋友有疑问,这道题能不能看两个图形之间的空格差距,
从左到右,按照2,1,0,
然后3,接着递减的话就是2,然后选择C
这里就凸显出为什么要先确定题目是考什么,明确图形特征的重要性了。
首先,看空格差距这个本身就不是规律,
这是一组图形,而不是两组图形,规律是一致的,递增也好,递减也罢,
中间数字不能忽然断开啊2,1,0,3,2,放在一起就不成规律。
另外空格差距也可以看成4,5,6,3,4这样看岂不是又要选择A?本身就不成规律,自然不对了。
所以我们先确定图形特征,明白考什么。
然后在从考点里面匹配题目,
自然会节省很多时间,也不容易错。
补充:
多宫格方向判定
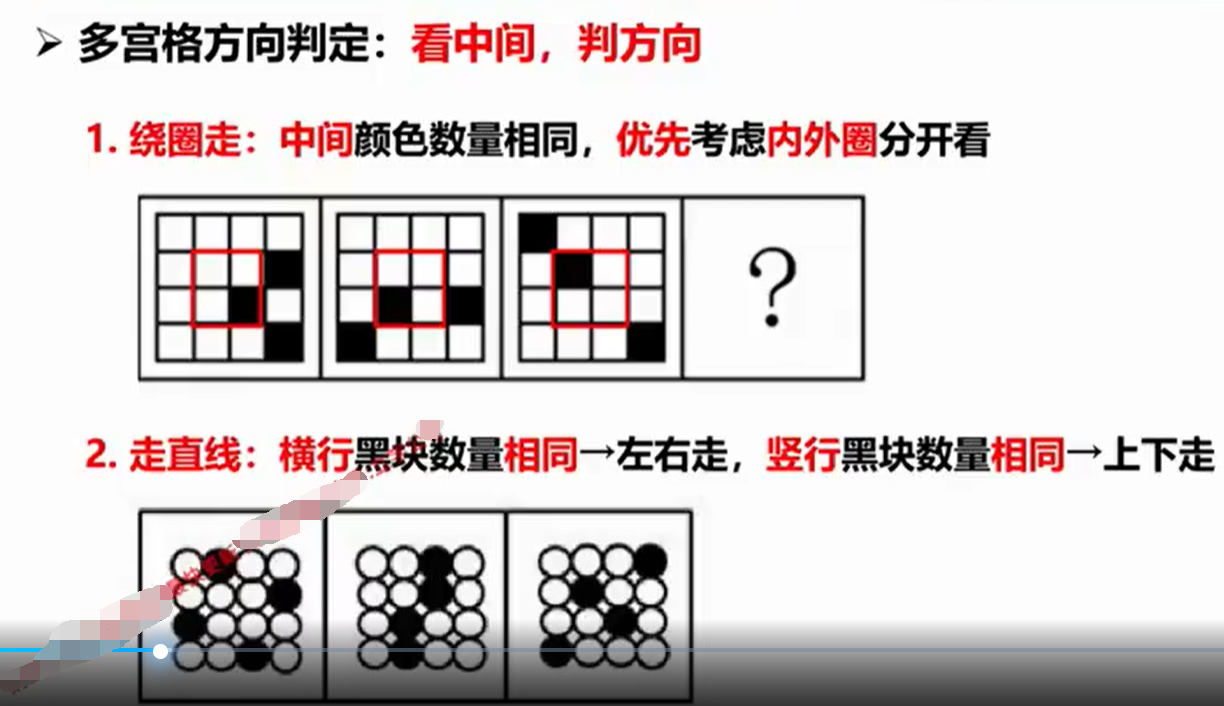
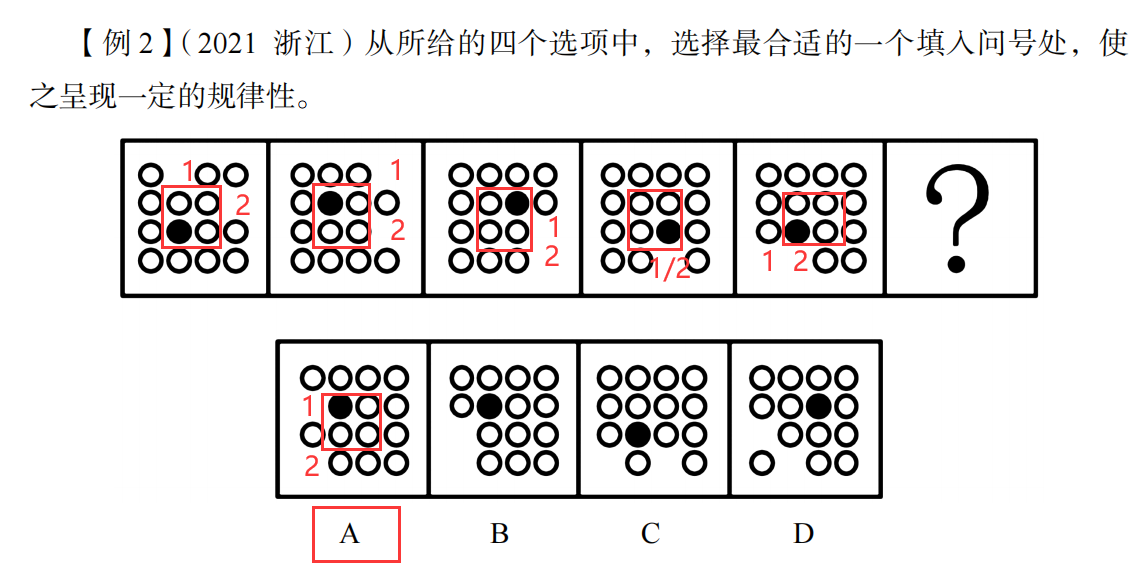
标号为1的图形每次顺时针走两格
标号为2的图形每次顺时针走一格
为什么在第二组图中不是1和2的位置对调呢?
不是说就近假设吗?
因为虽然看起来2更近,但是这样的话,下一组图里面,1移动的格数太多了,
所以我们不就近假设2
另外如果按照第二组图2,1位置对调的话,后面也会发现是不符合规律的。
这属于做题经验,做得多了自然就会选择最有利的方式了。
走重合判定

可能会出现第一组图是两个黑球,然后第二组图是一个黑球。
但是不会出现第一组是一个黑球,第二组是两个黑球的情况。
因为有争议,所以不会这样出题。
这道例题是经典的走重合和多宫格方向的综合应用。
再看一道例题:
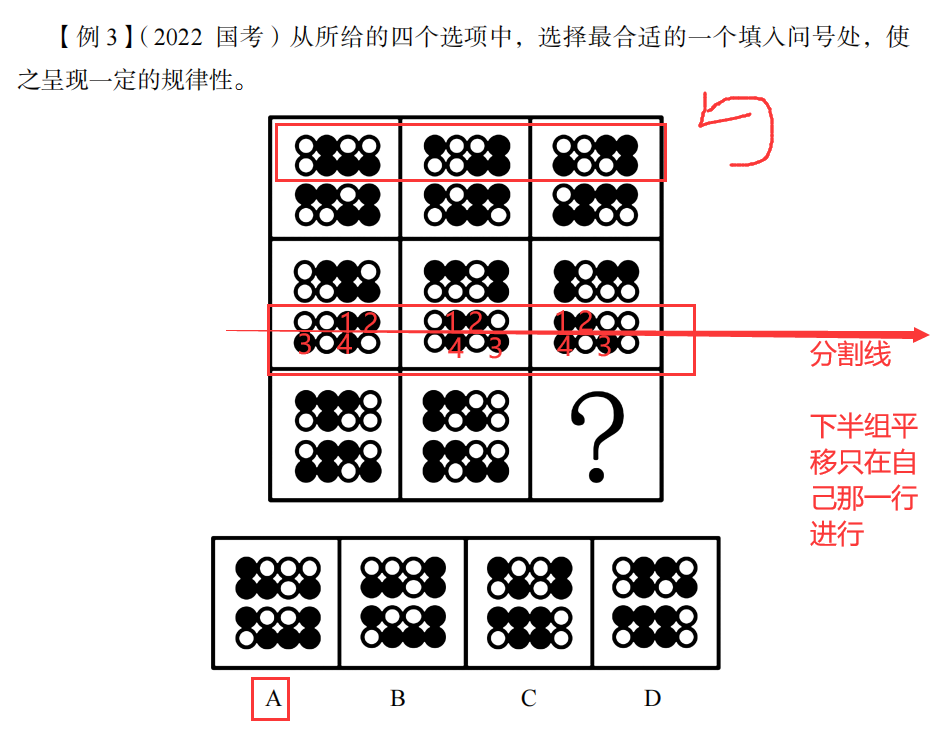
首先,图形特征是:组成元素完全相同
然后分开看,一个格里面看成上下两部分。
上半部分是每次逆时针走一格
下半部分是每次向左平移一格
注意:
小球向右平移,会有两种情况:
①从左往右平移,平移到头之后,再从起始开头点从左往右平移。
②从左往右平移,平移到头之后,被弹回来,开始从右往左平移
做题优先考虑第一种情况,因为出的题比较多。
实在不行再考虑第二种情况,出题比较少。
①从左往右平移,平移到头之后,再从起始开头点从左往右平移。

即1,2,3,1,2,3,1,2,3
②从左往右平移,平移到头之后,被弹回来,开始从右往左平移

另外,考试大多数都是考的黑球的规律,白球也有,但是很少见。
②旋转、翻转

例题:
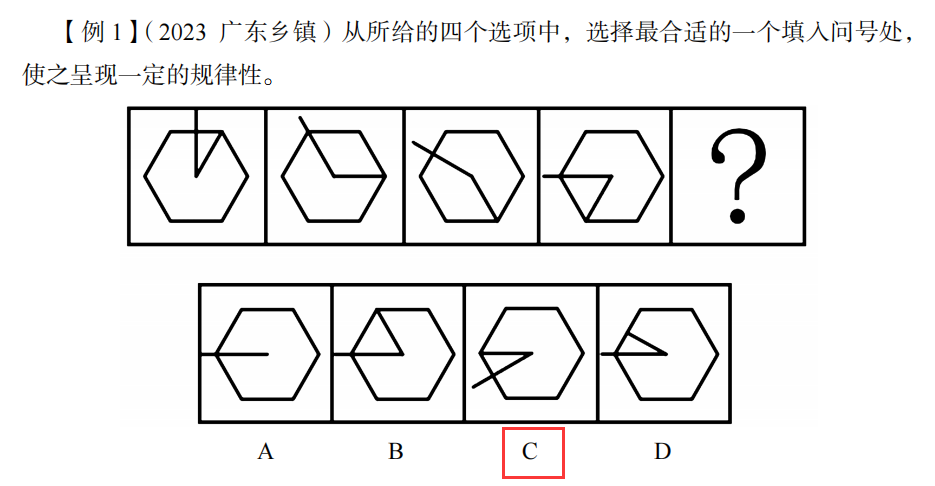
长线每次逆时针转动30度
短线每次顺时针转动60度
例:
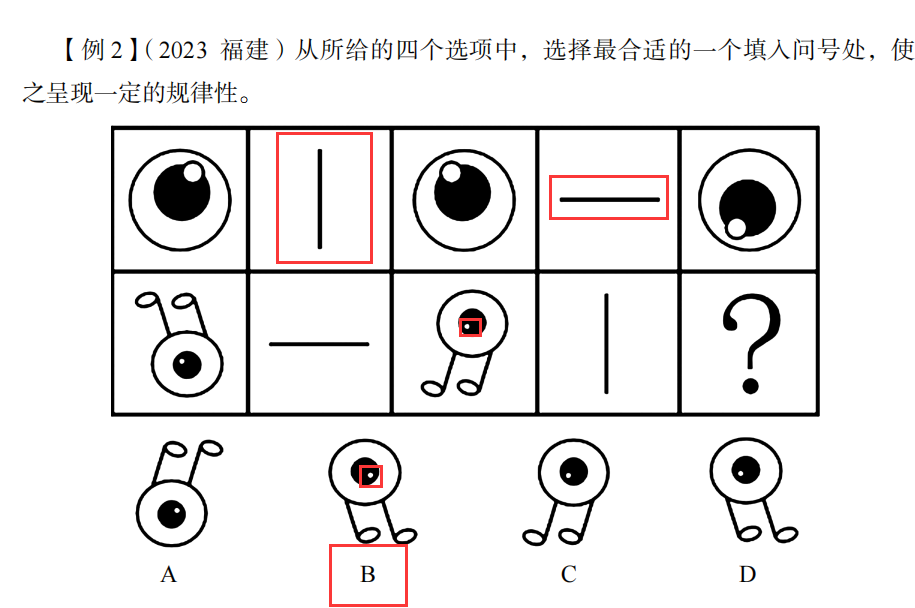
第一幅图和第三幅图是关于第二幅图对称的。
也就是说相邻的图是以中间的图为对称轴得到的。
注意小白点。
重难点
两组图或九宫格,考旋转或翻转——找对称
(比如,第一幅图和第三幅图,对称,至于第二幅图是如何变到第三幅图的可以不去管他)
(2)样式规律
①遍历

考法:
1.形状遍历
2.颜色遍历
3.位置遍历
例题:
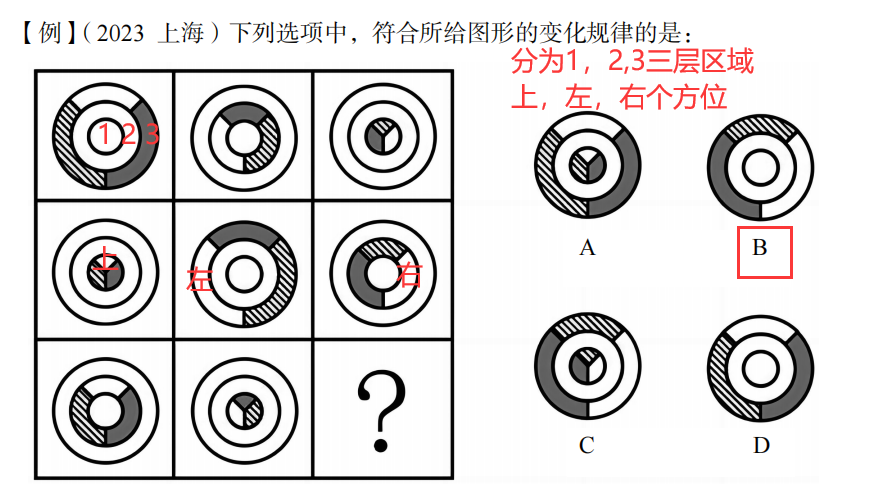
题干每一行图形长得很像,但不完全一样,即元素组成相似,考虑样式规律。
每幅图均有3个区域,且每一行三幅图每个区域分别有颜色。
第一行:图1只有最外圈有颜色,图2只有中间一圈有颜色,图3只有最里圈有颜色。
第二行:颜色依次在最里面、最外边、中间层。
第三行:颜色依次在中间层、最里面、缺少最外面。
A、C项最外层、最里面都有颜色,均排除。
第一行:白色在上面、左面、右面
第二行:白色在上面、左面、右面
第三行:白色在上面、左面
所以最后一幅图应该是白色在右面。
排除D选择B
当然竖着看也可以,并且对于这道题来说的话,竖着看解题更快。这里主要讲解了横着看的,因为大多数题目还是考的横着看的。
②加减同异

例题:
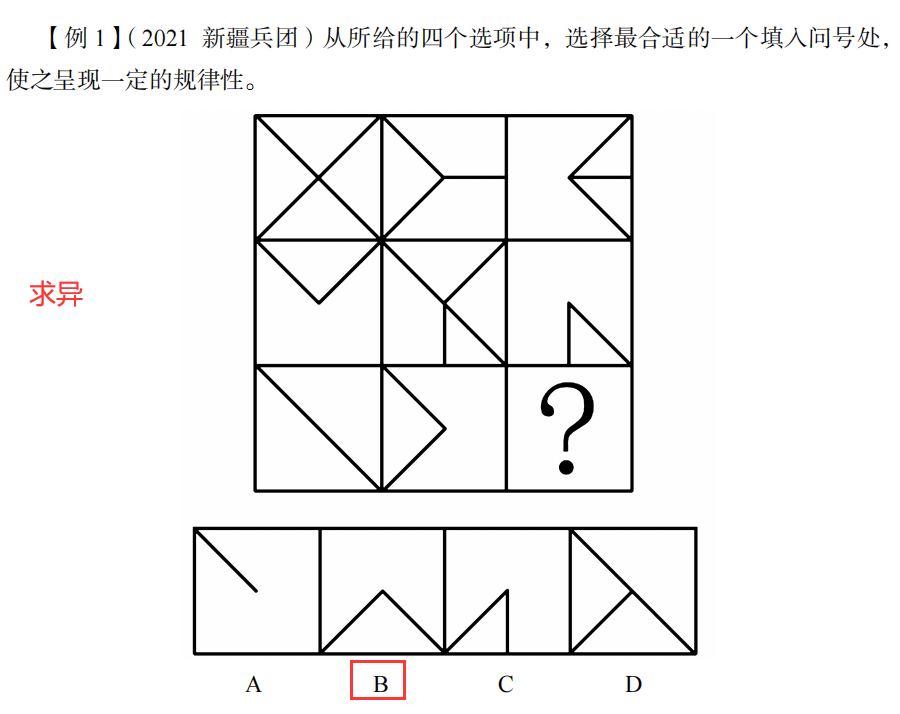
九宫格,每一行,求异,去掉相同的线条,留下不同的线条。
补充:
加减同异难点——结合位置规律
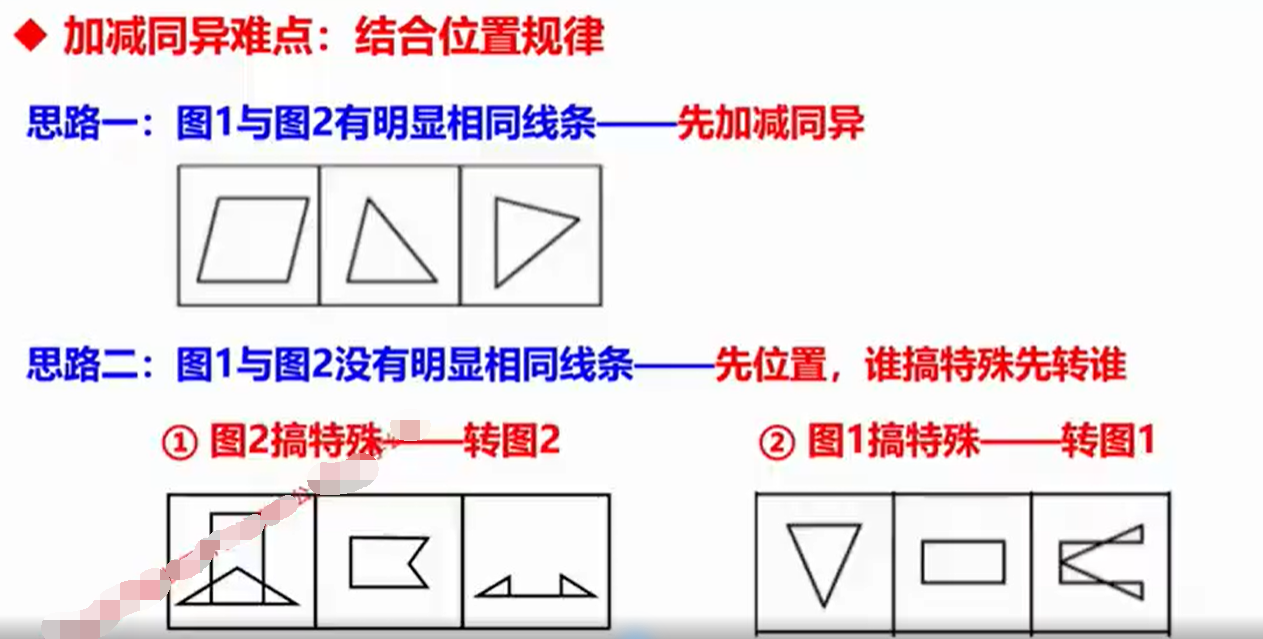
关于思路二,谁特殊怎么看?
比如①,一组三个图,图一和图三的相同线条最多,所以图二是特殊的,转图二。
②,一组三个图,图二和图三的相同线条是最多的,所以图一是特殊的,转图一。
看谁特殊,是于图三相比的。
例题;
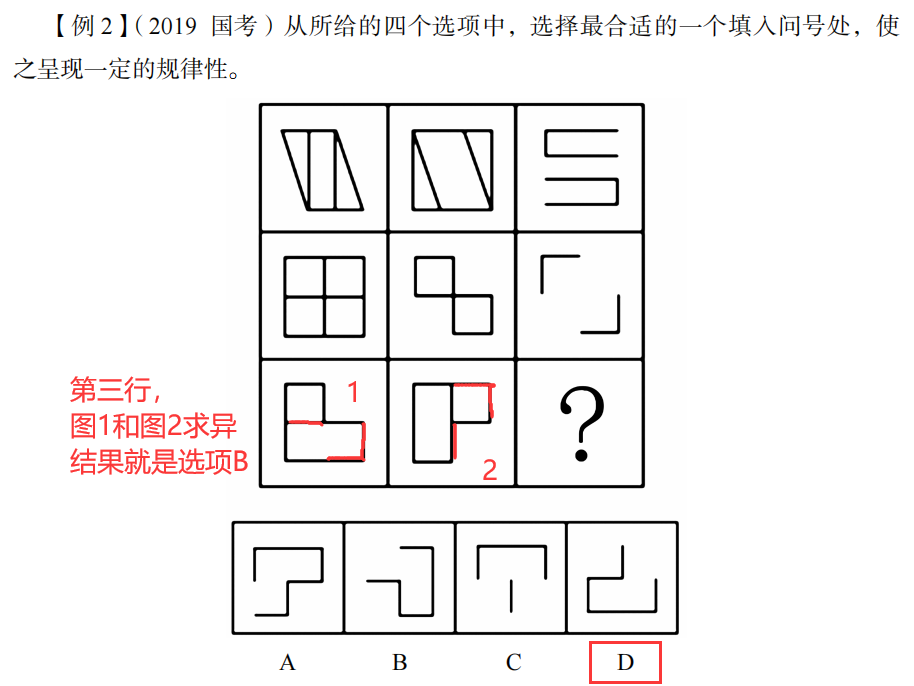
规律:
前两个图求异,求以后的结果图顺时针或者逆时针选旋转90度,得到第三个图。
分析选项,选择D
③黑白运算

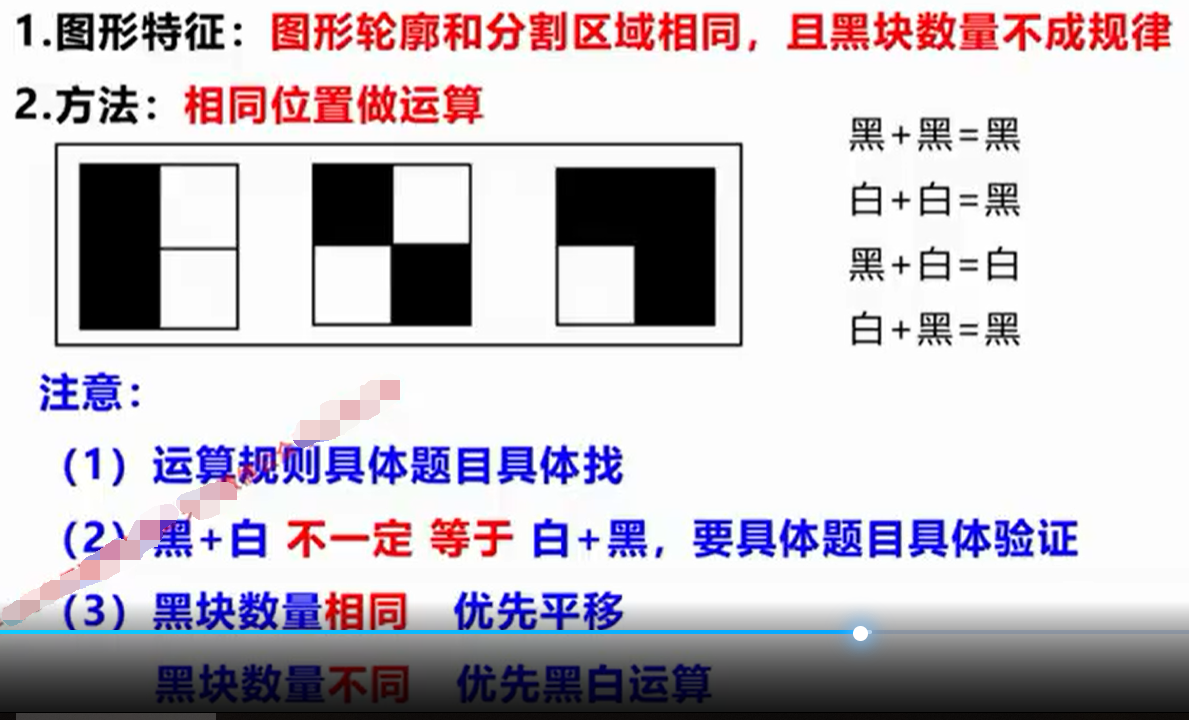 第一组图得出规律,第二组图验证规律,第三组图应用规律。
第一组图得出规律,第二组图验证规律,第三组图应用规律。
技巧:优先找大面积相同的色块进行运算,可以帮助快速解题。
什么叫做图形区域相同?
比如:

图一的区域是矩形,图2的区域是椭圆,二者的图形区域不同。
什么叫做分个区域相同?
比如:
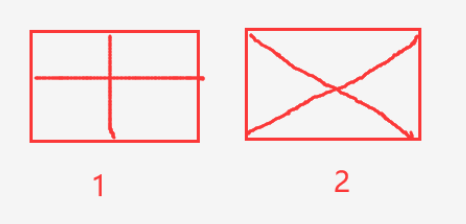
图1和图2的图形区域相同,但是分割区域不同。一个是“十字分隔”,一个是“X分隔”。
例题:

从第一组图可以得出规律:
黑+黑=白
黑+白=白
白+白=黑
白+黑=白
直接秒选A
(3)属性规律
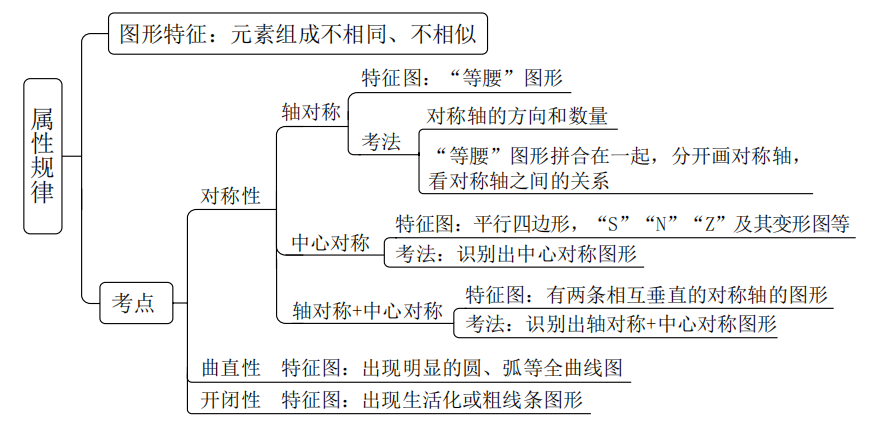
①对称性

考法:
1.区分 轴对称/中心对称/轴+中心图形,对其进行分类
2.对称轴的方向与数量
牢记“对称轴数量”的题目特征——等边三角形(三足鼎立)
3.多个等腰图形拼接,分开画轴,考查轴与轴的位置关系
4.对称轴与图形线、点、面(经过几片区域)的关系
思路:每幅图均只有一条对称轴且方向选不出答案时,考虑此法。
养成好习惯,发现轴对称图形立刻画出对称轴。
注意!!!
不能把轴对称图形和非轴对称图形分为两类去做题。
轴对称图形非轴对称图形两大类包含太广,根本就没有规律。
所以不能这样去做题。
例题:
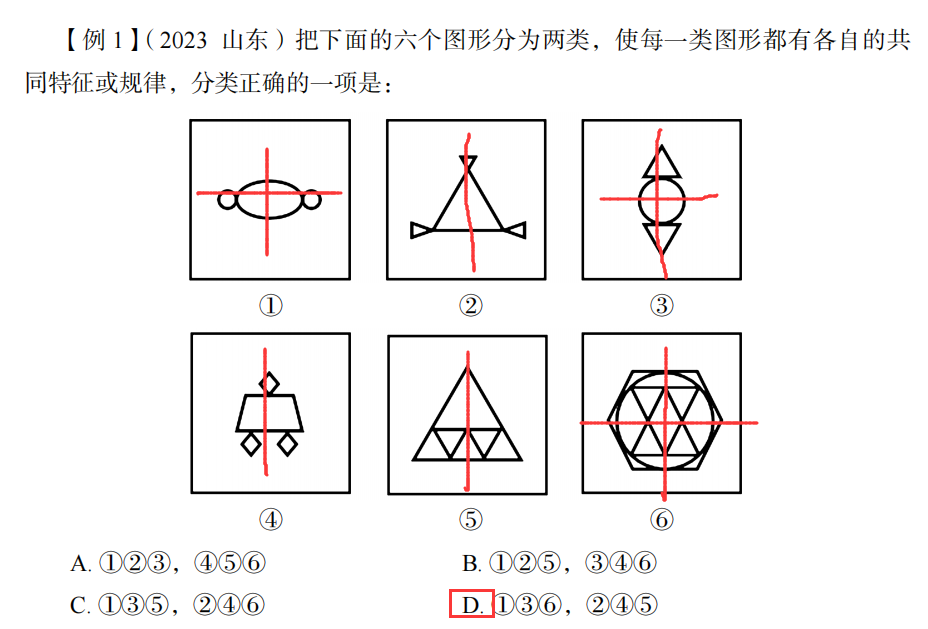
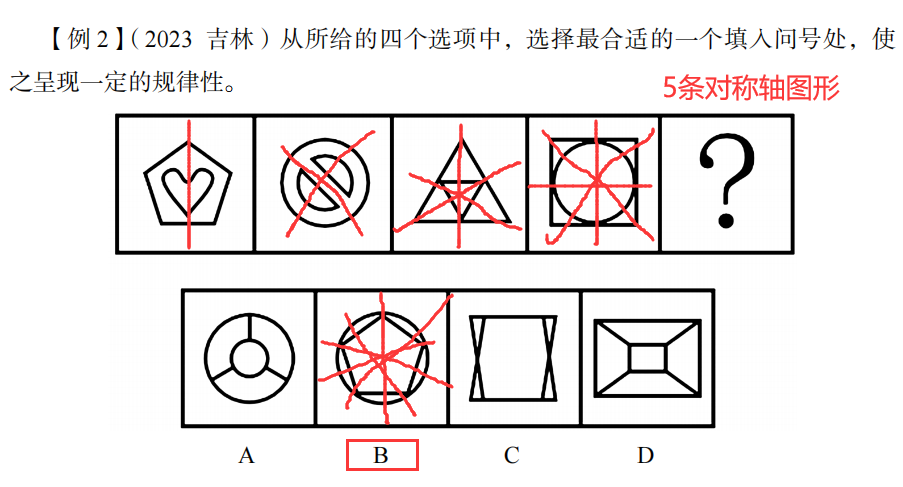
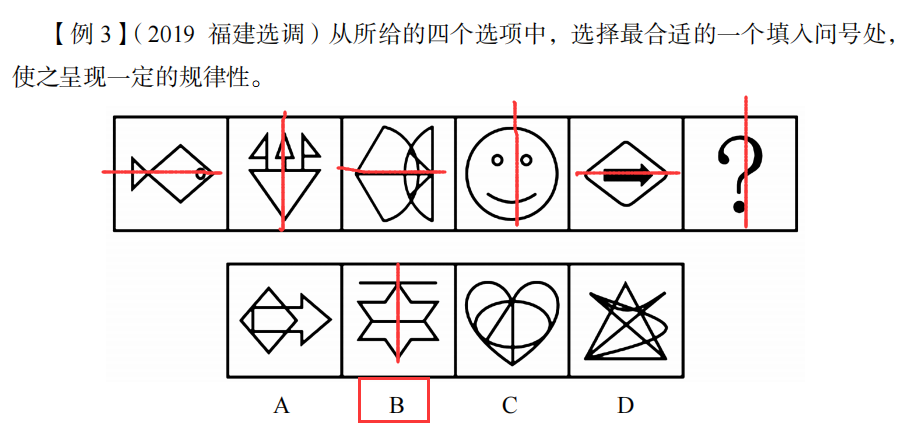
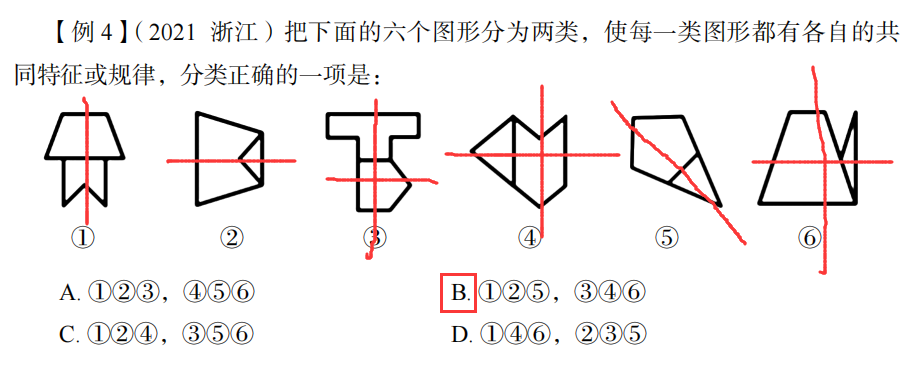
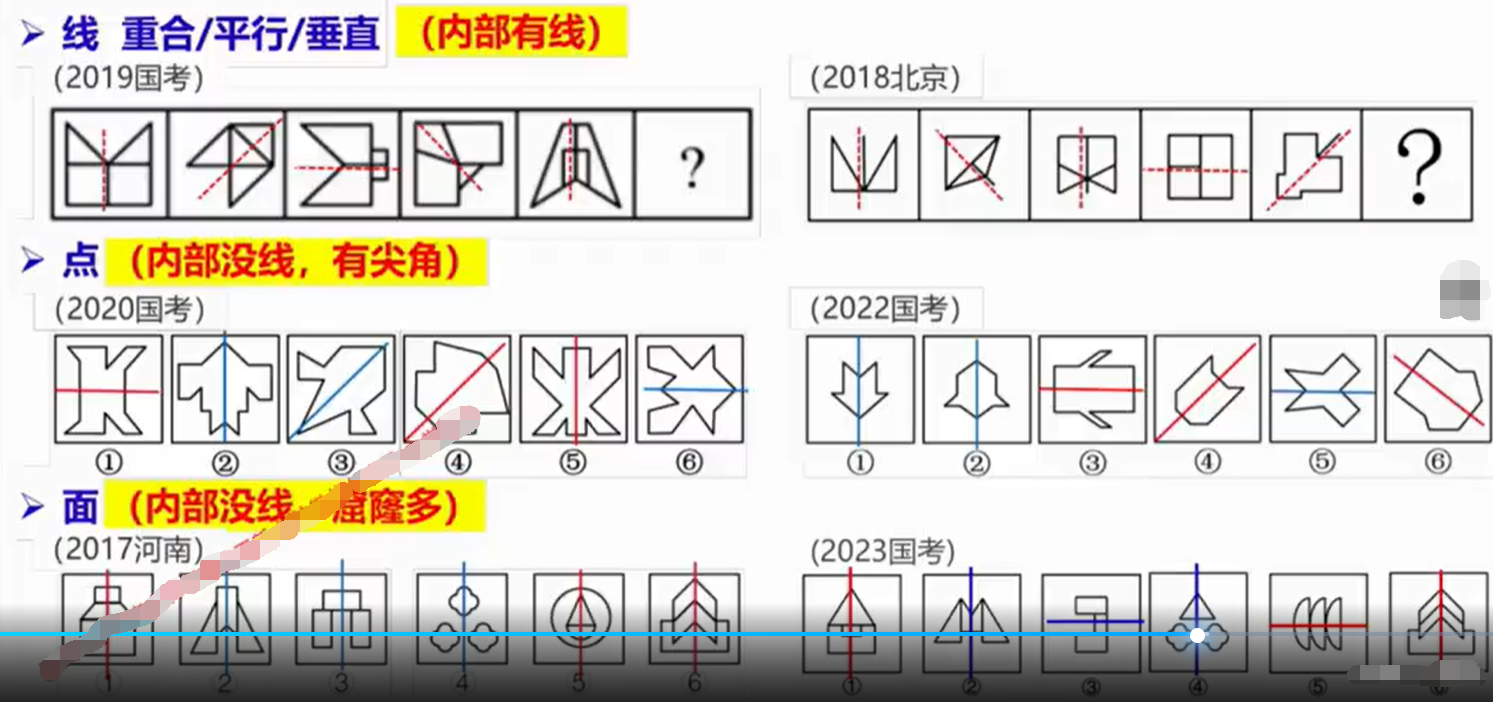
①②⑤图形的组成图形的对称轴重合
③④⑥图形的组成图形的对称轴垂直
例题;
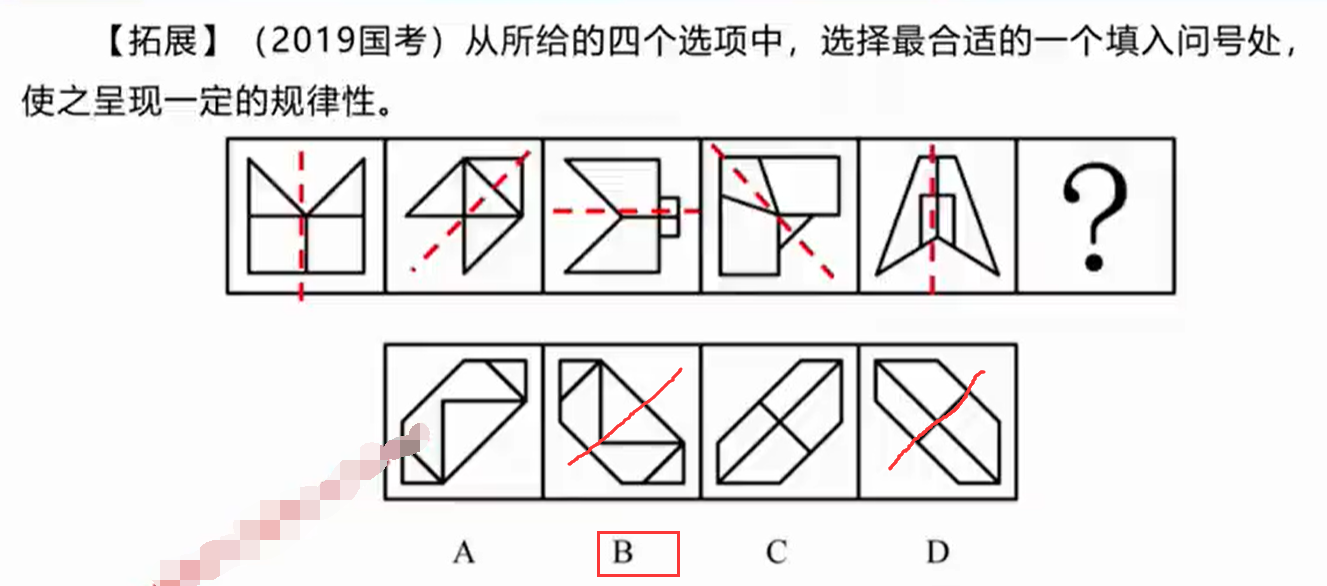
图1,3,5的对称轴都和图形的一条线重合,
图2,4的对称轴不和图形的线重合。
所以图6的对称轴也不应该和图形的线重合。排除D
选择B
补充
对称轴与图形线、点、面(经过几片区域)的关系
思路:每幅图均只有一条对称轴且方向选不出答案时,考虑此法。
注意:
1.过了几个交点指的是对称轴过原图形中的交点(原图形两条或者以上线段相交的交点),而不是对称轴与原图形有几个交点。
2.对称轴过了几个面,可以理解为过了几片区域(因为严格来说平面图形只有一个面的)
比如:
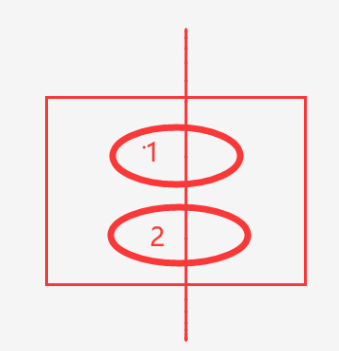
上图中对称轴过了两个面(方格是给的,不要考虑在内)。
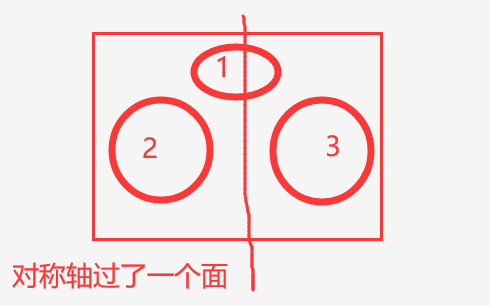
上图中对称轴过了一个面。
②曲直性

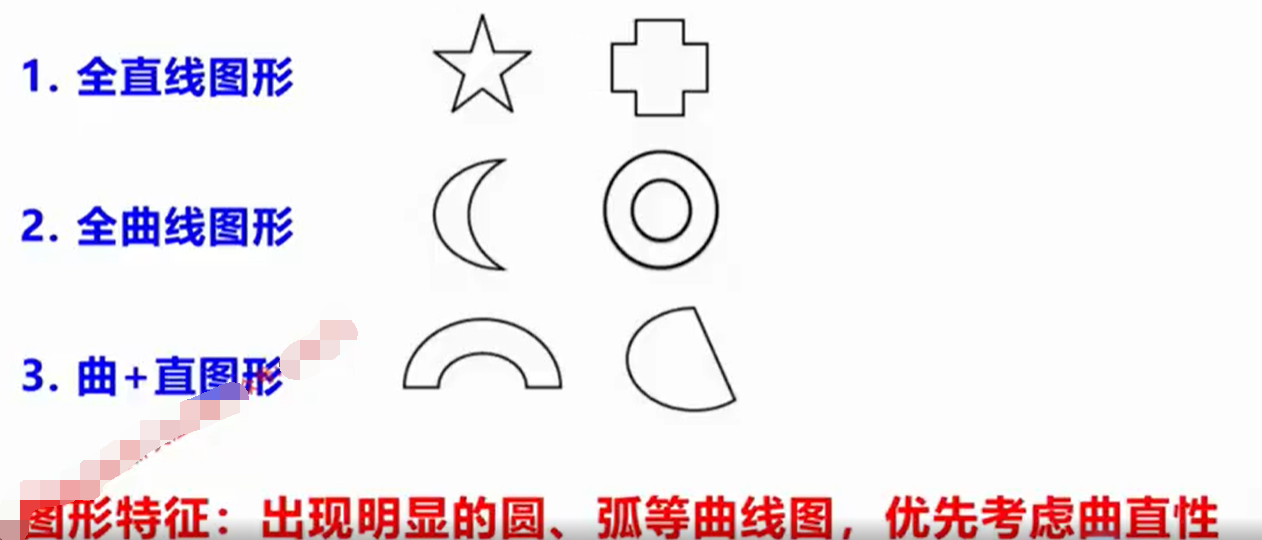
例题:
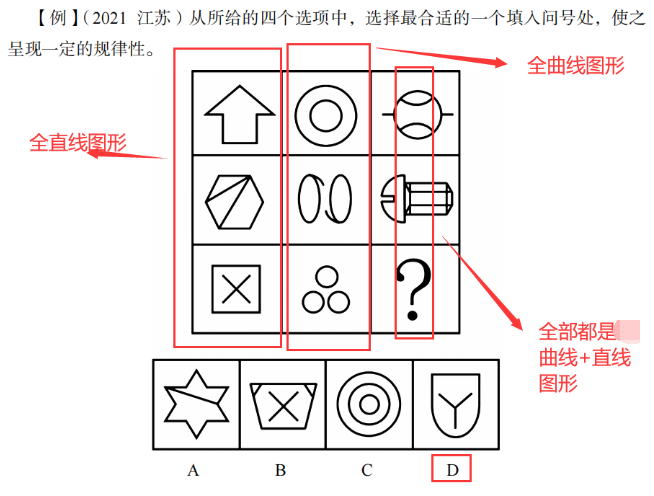
③开闭性


什么叫做生活化或者粗线条图形?
比如上图中的手,是生活中的图标,这种的就叫做生活化图形,
它同时也是一个粗线条图形。
手上面的那个四方块就属于粗线条图形,上图那个未封闭的圆属于细线条图形
例题;
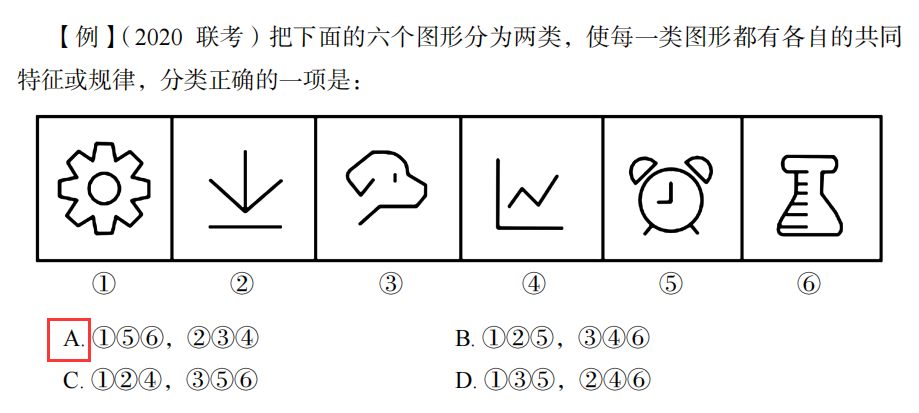
注意:
这道题其实是有争议的,闹钟那个图形实际是半开半闭图形。
但是没办法,只能这样选择,有封闭就行。
(4)特殊规律
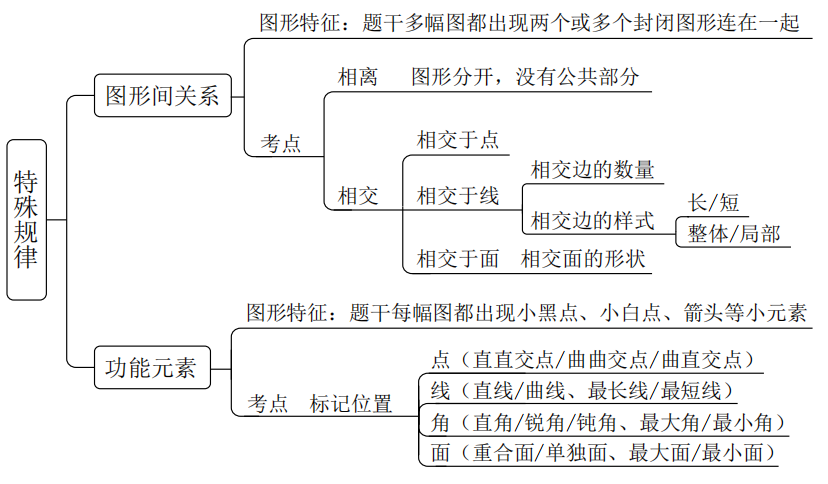
①图形间关系

注意:

例题:
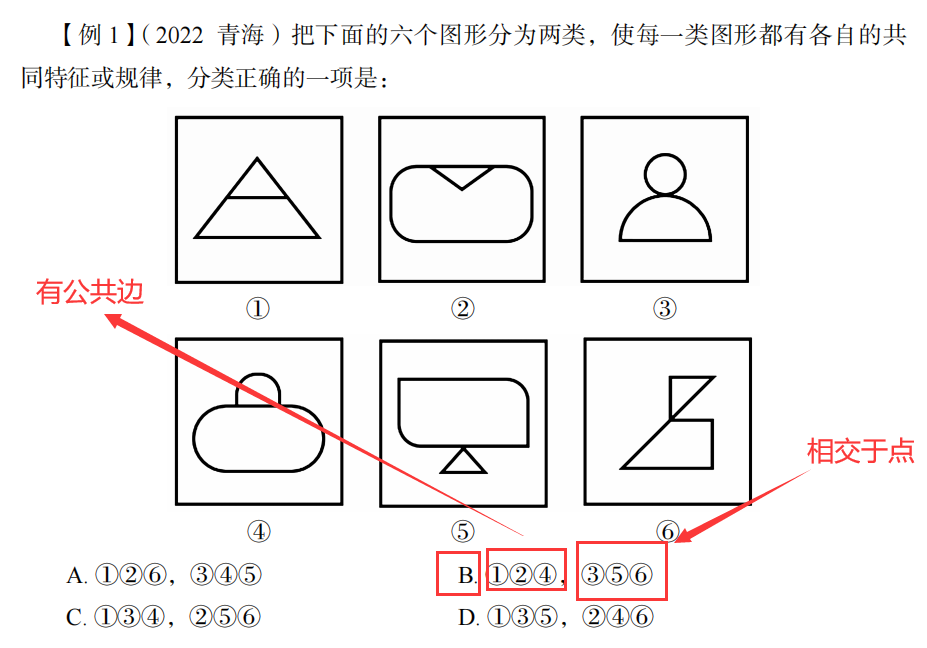
补充:
相交于线的细化考法
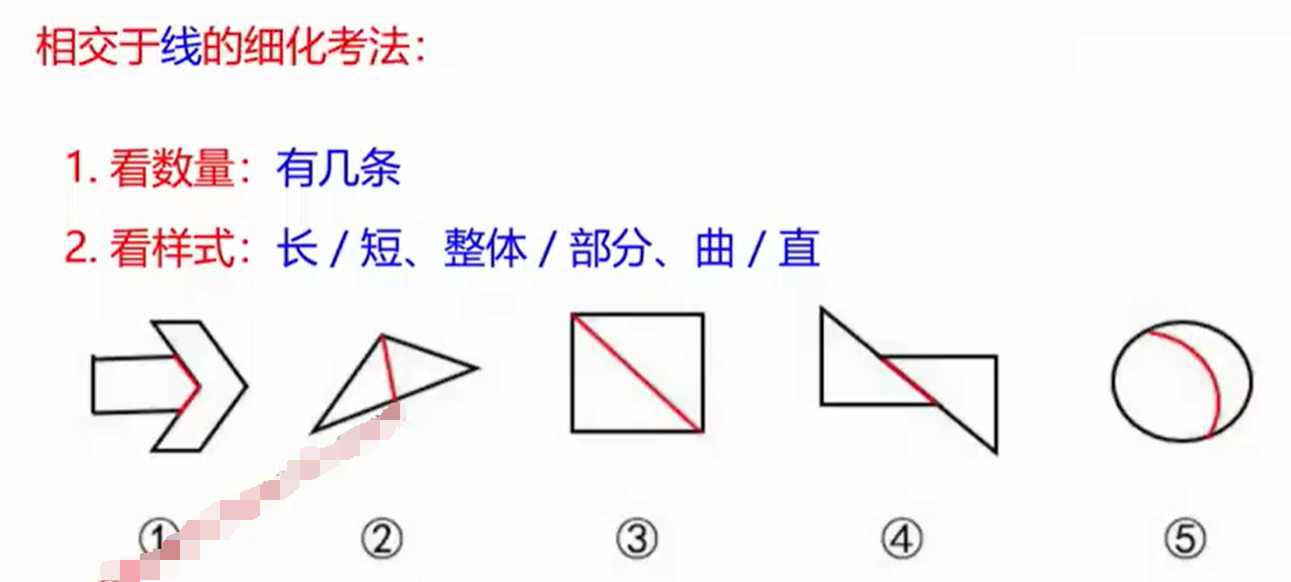
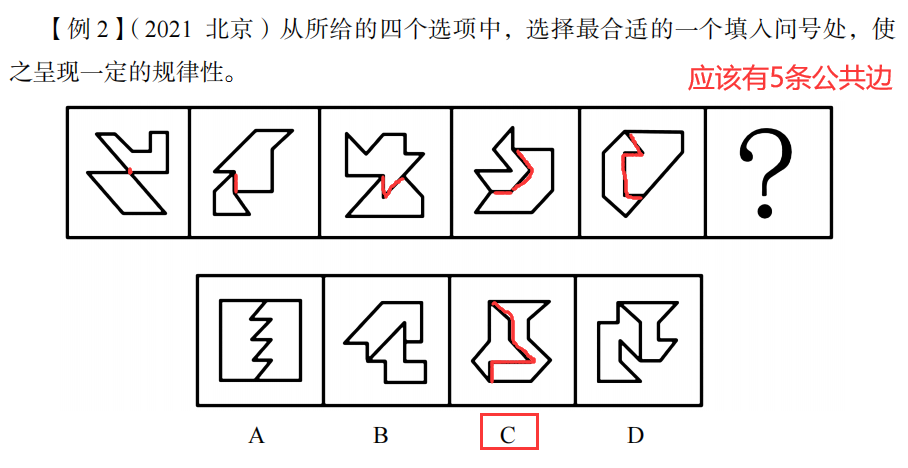
例题:
相交于面的细化考法
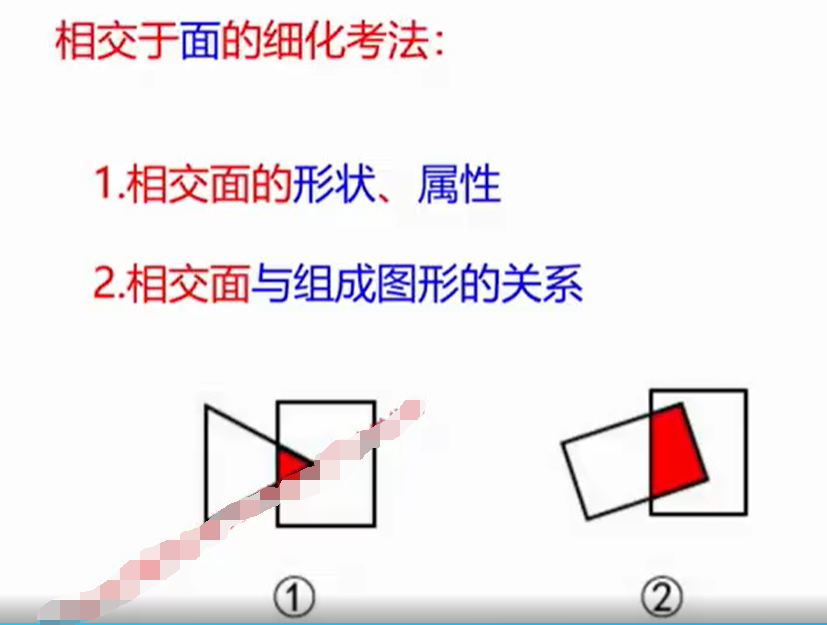
1.相交面的形状和属性
比如:
形状:图①相交面是一个三边形,图②相交面是一个四边形
属性:图①相交面是一个轴对称图形
2.相交面与组成图形的关系
图①相交面是一个三角形。和其中一个原图形相似。
例题;
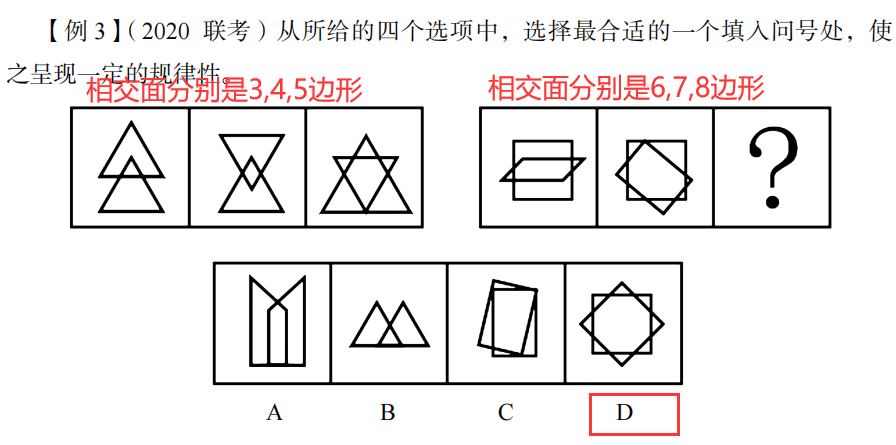
②功能元素(标记作用)

例题;
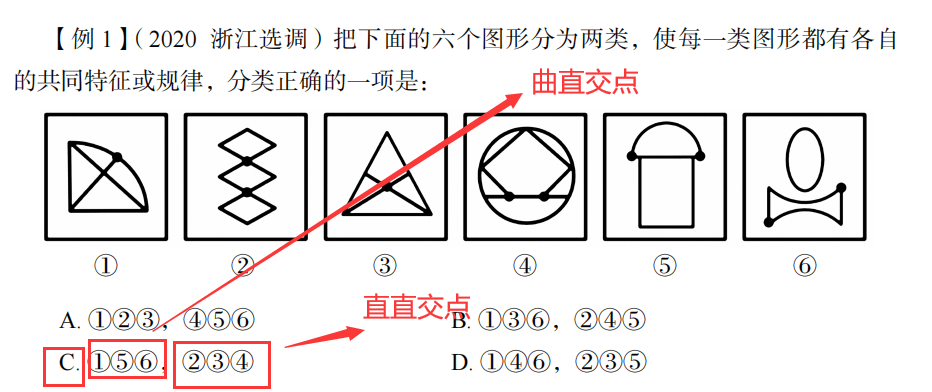
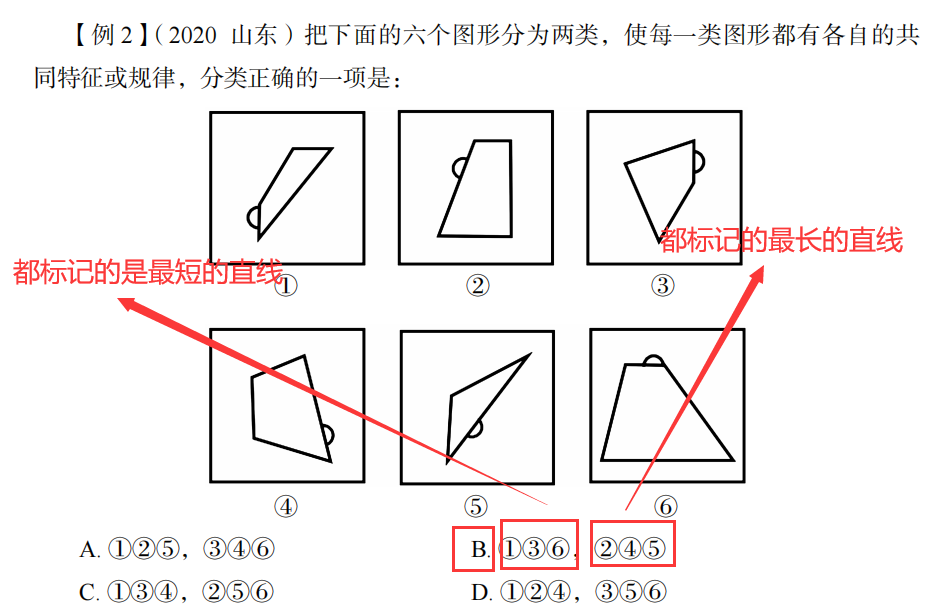
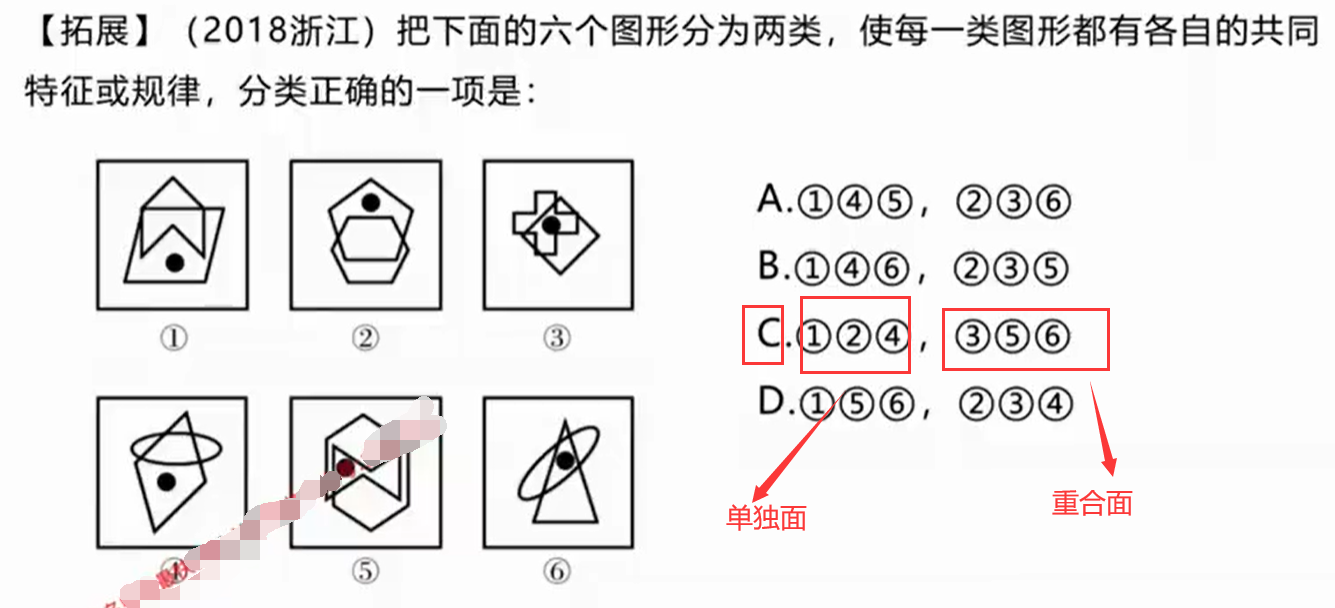
(5)数量规律
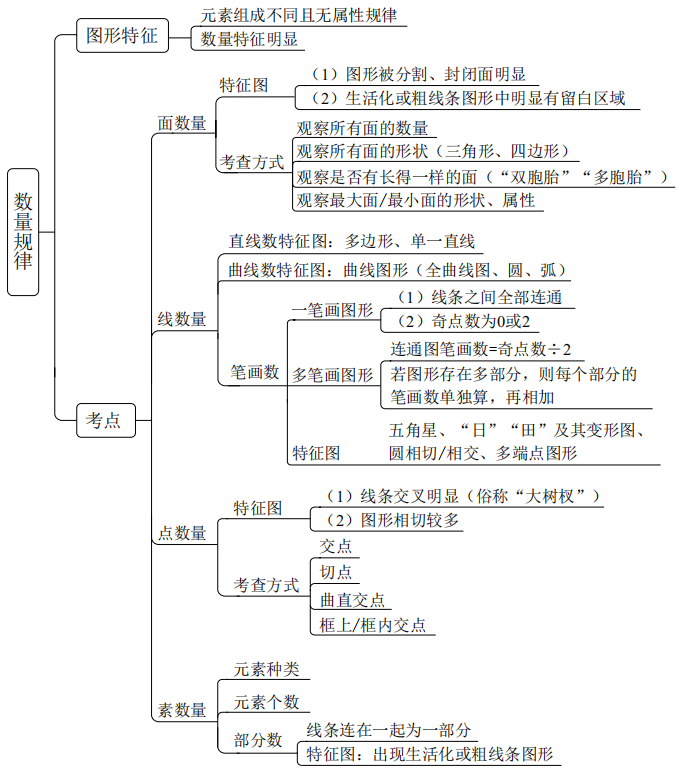
角很少考,这里就先不讲了。
①面数量

什么是面呢?
白色的封闭区域叫做面。
注意,面是白的,黑色的不是面!
什么时候数面?
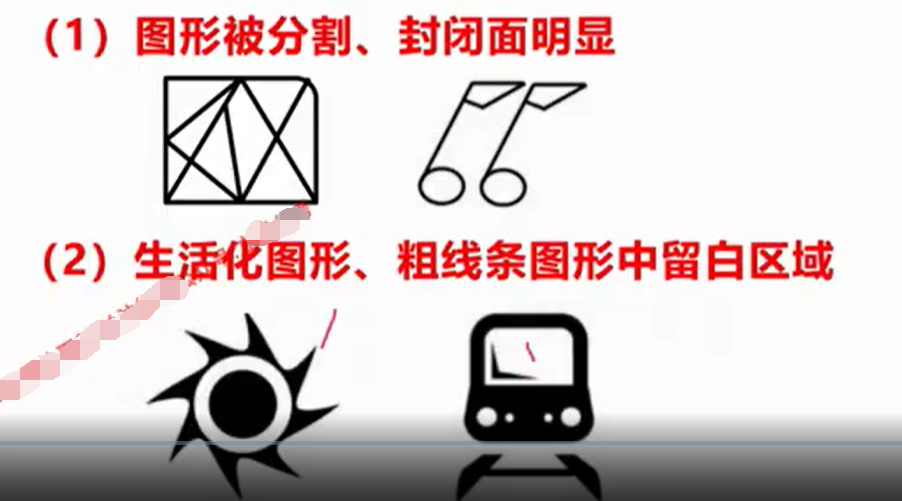
例题;
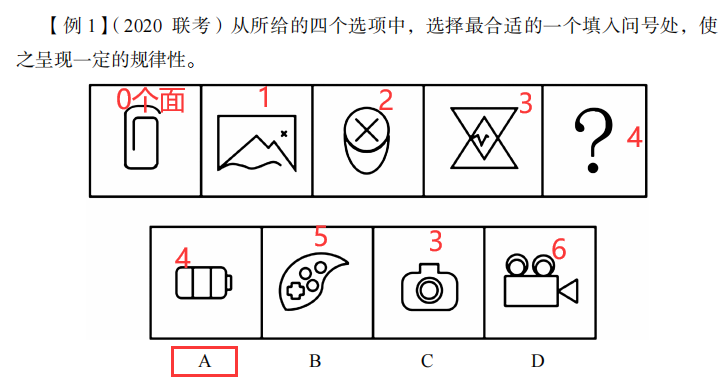
补充:
面的细化考法:
什么时候想细化?
出现数面特征图,整体数面选不出答案的时候。
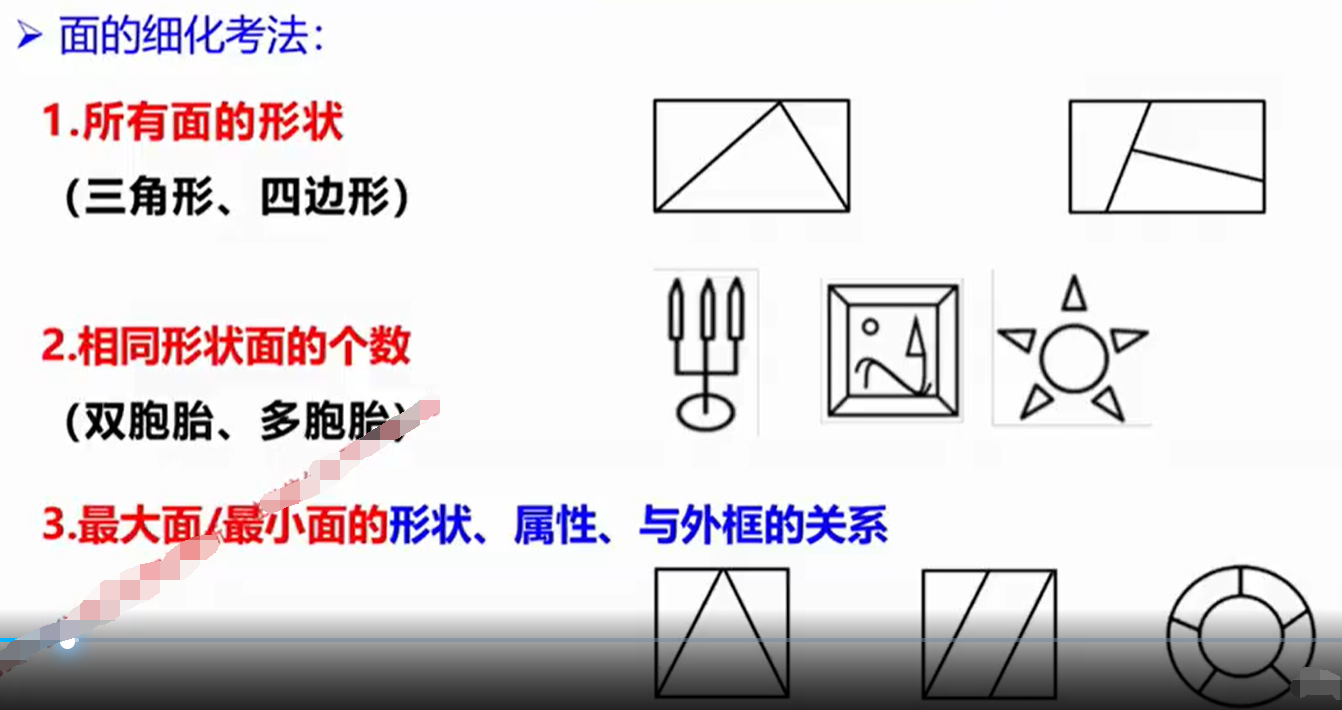
例题:
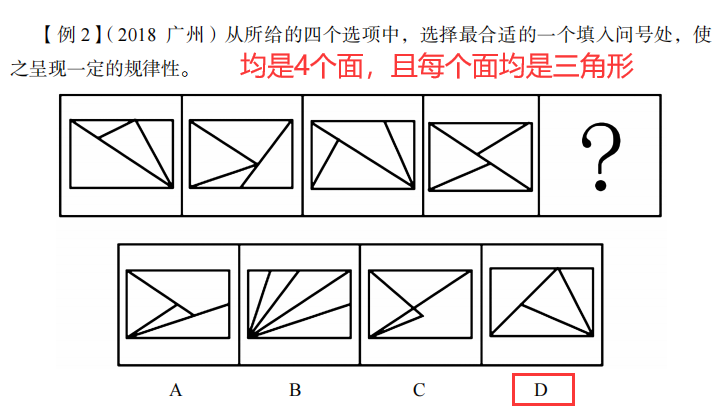
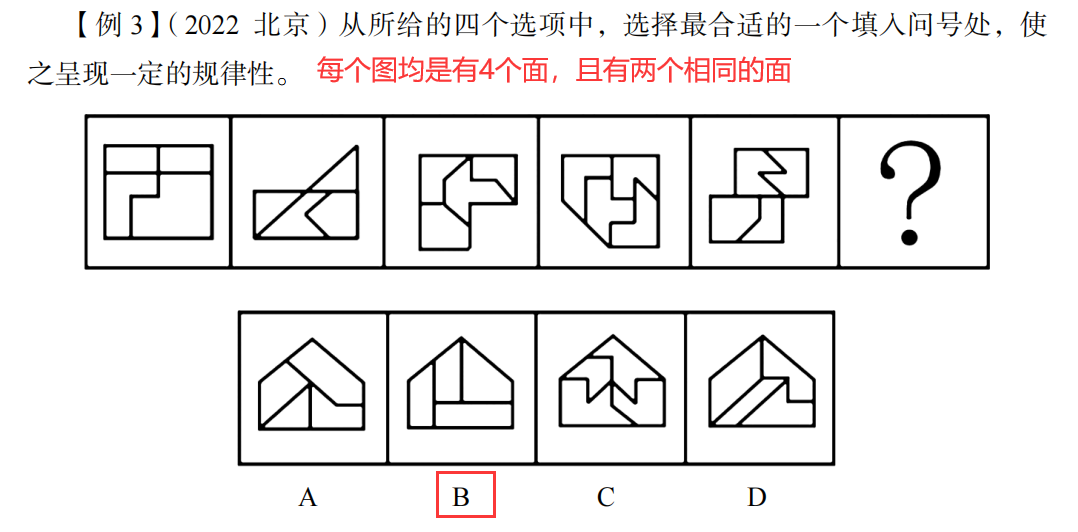
注意:
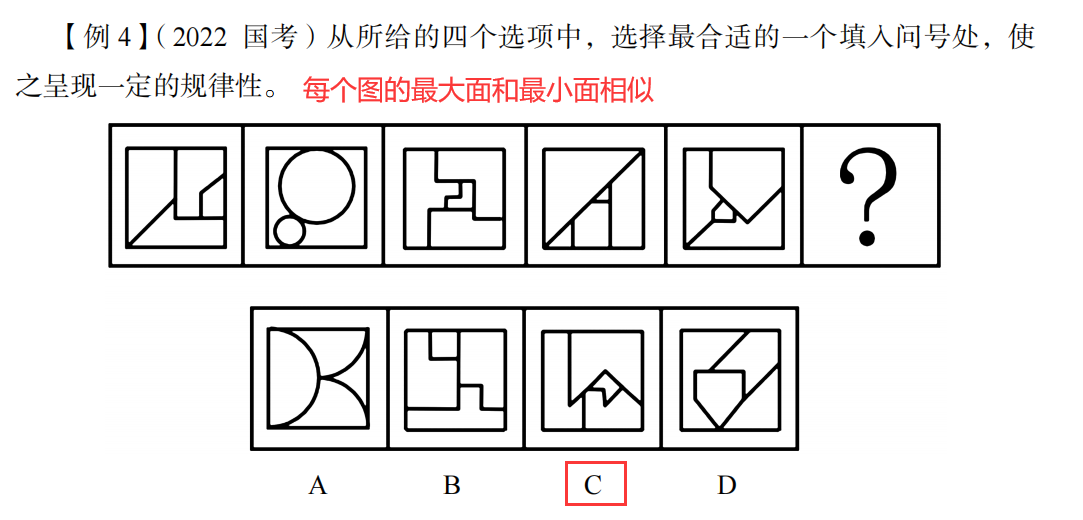
当某一个面“特别大”时,考虑最大面和最小面。
例题;
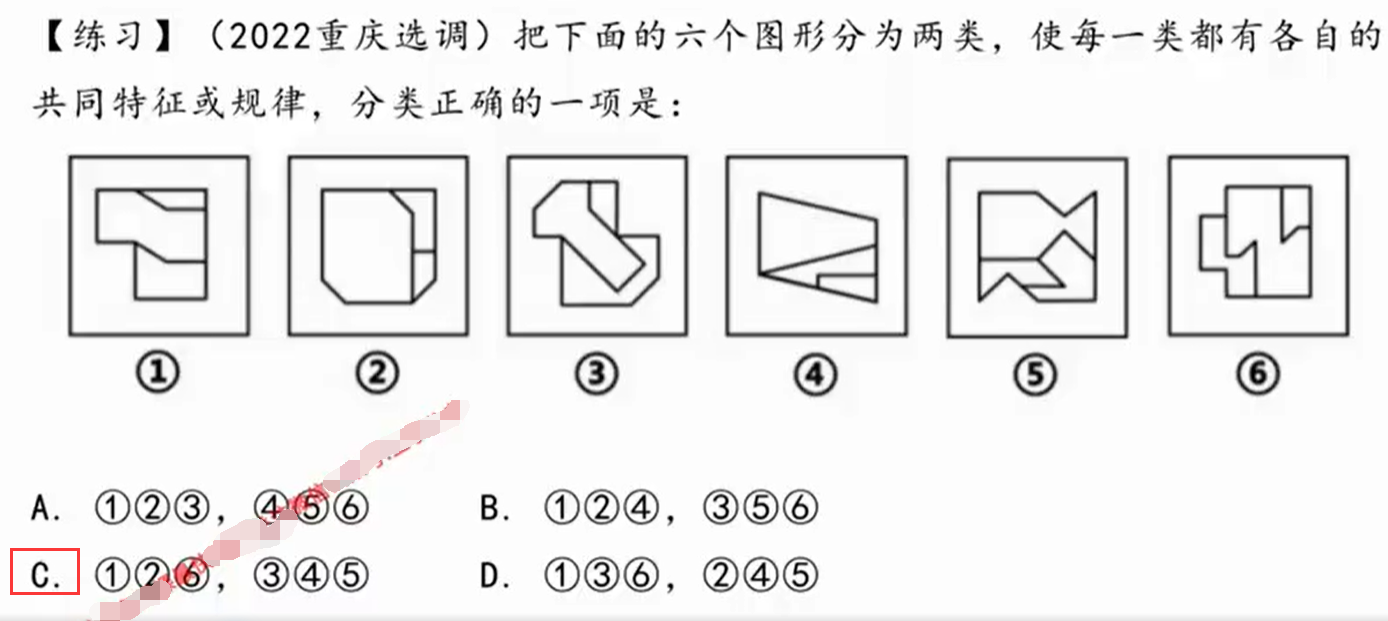
最大面:
①②⑥是中心对称图形
③④⑤是轴对称图形
②线数量

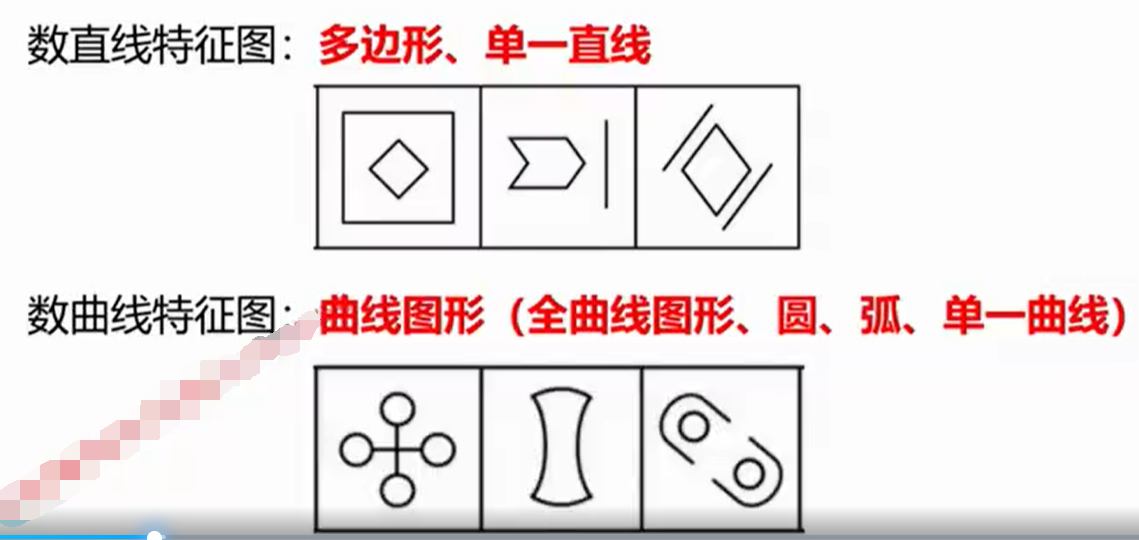
怎样算一根线?
平滑的、没有折点的叫一根线。
注意:直线不等于线段,计算的是直线的数量。
例题;
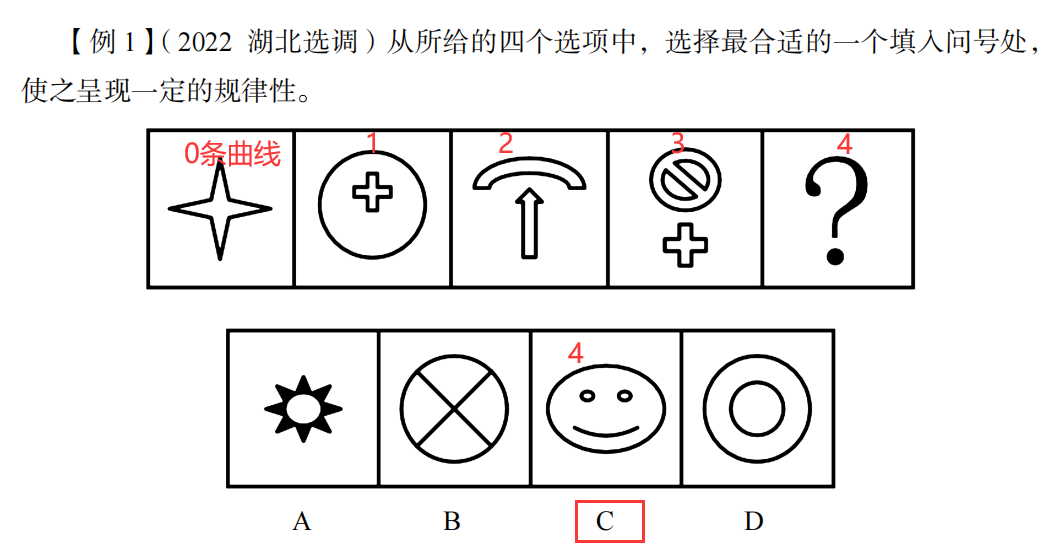
另外:
关于A,A图形没有曲线。那个看起来是白色的圆的是由八个小图形的一部分弧组成的。
比如,一个月亮,有两条曲线。
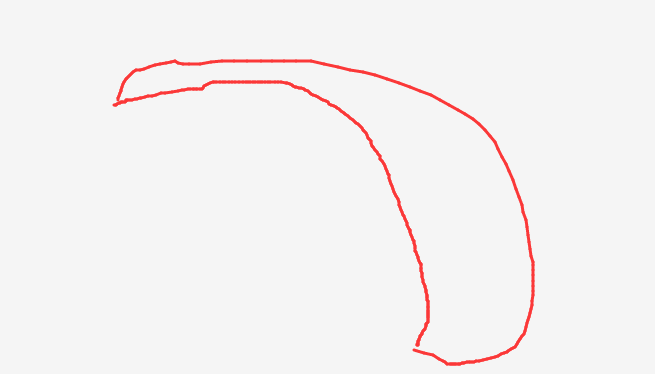
但是,如果他是涂黑的月亮,那就没有曲线。
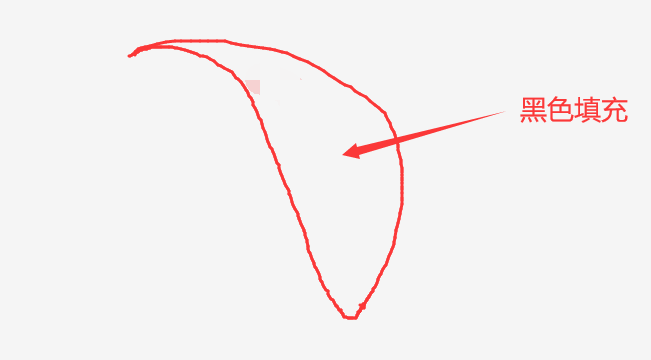
切记!!!
任何图形被涂黑之后,曲线和直线数量都为0
例题:
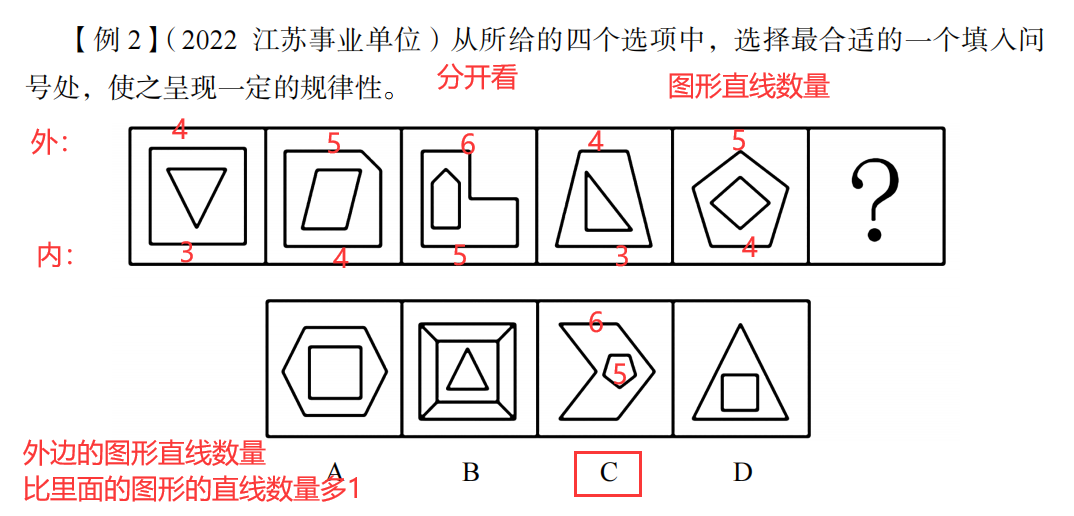
**注意:**不能按照7.9.11,7,9,11去做题,这种周期规律不算是规律。
一组图形的,只有两种方式,横着顺着规律,或者是间隔成规律,没有周期规律。
例题;
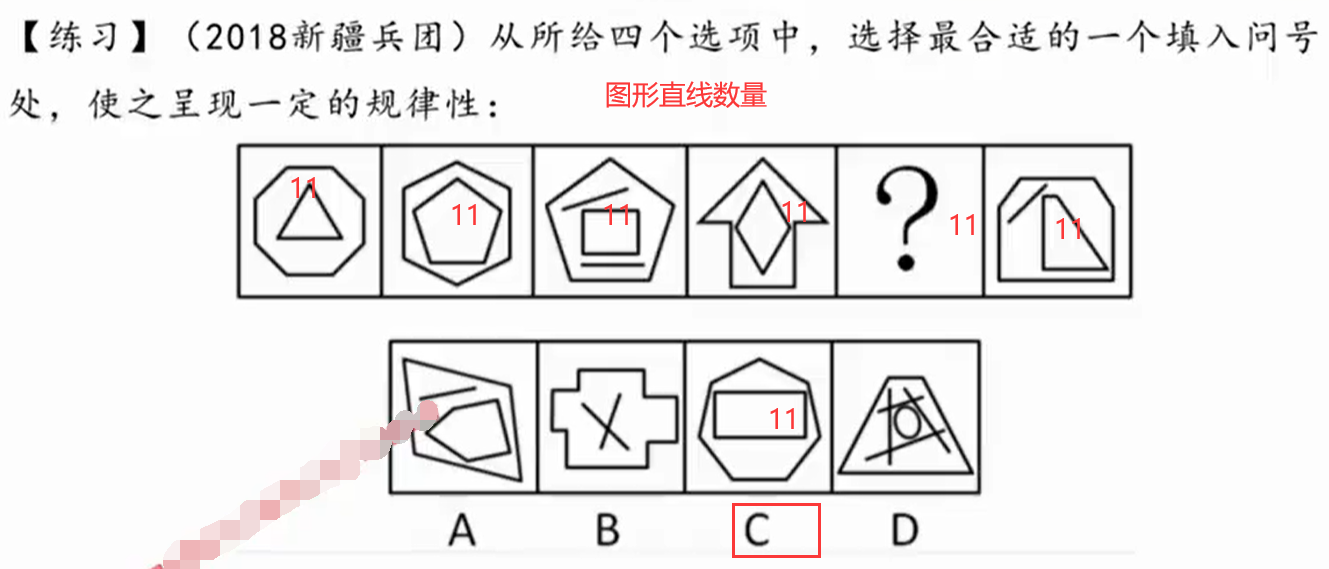
补充:
笔画数
一笔画图形概念:
在不能重复的情况下,能够一笔画成的图形。

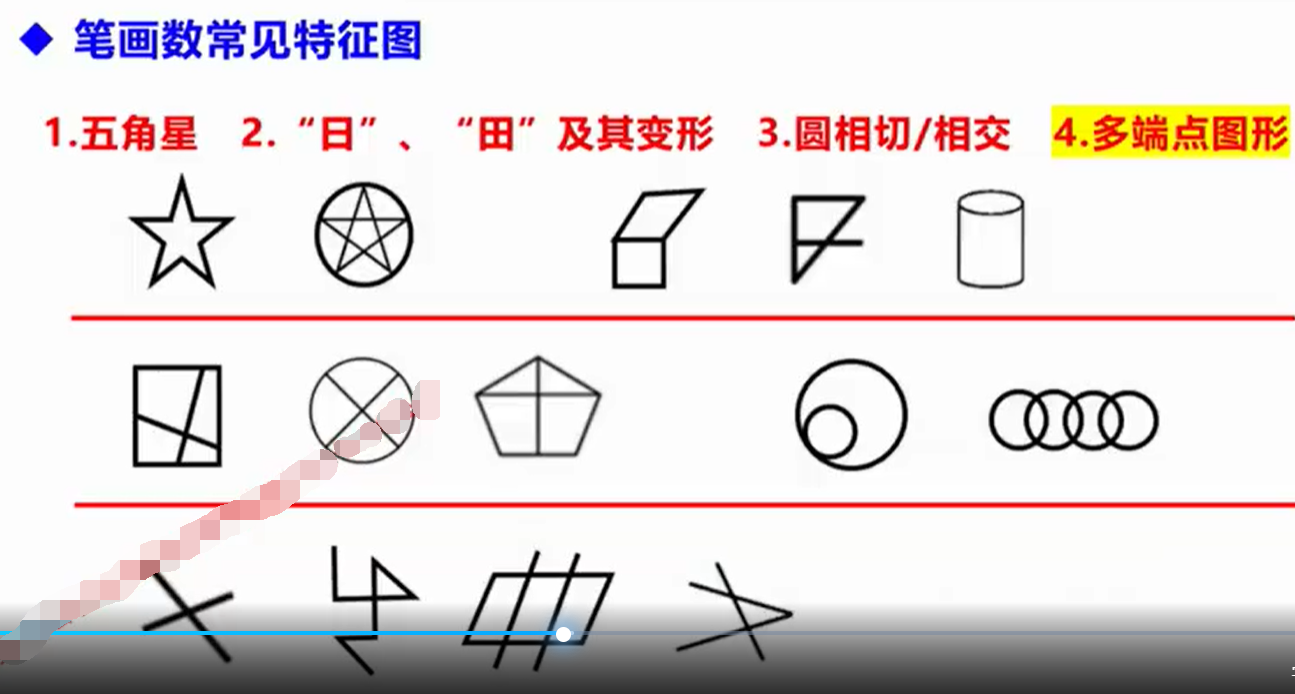
例题;
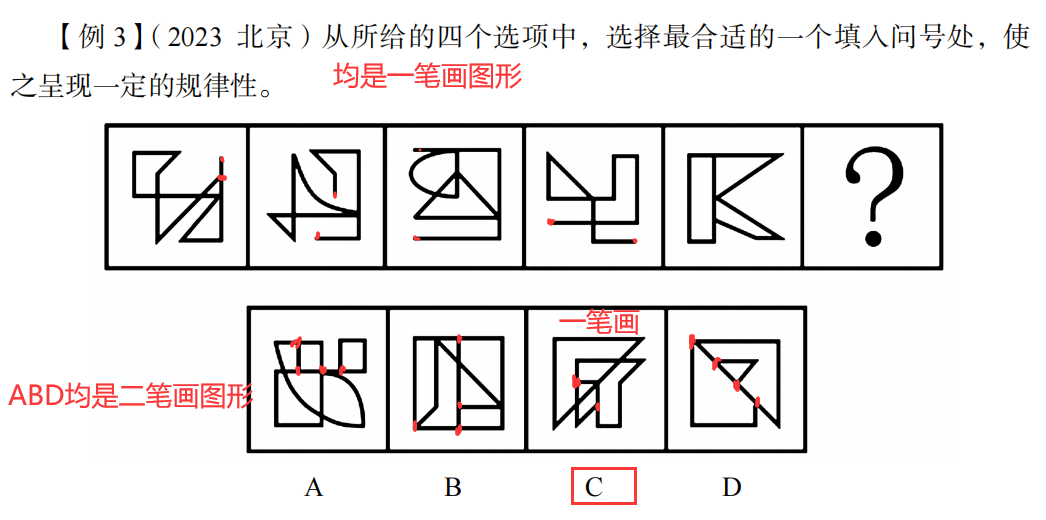
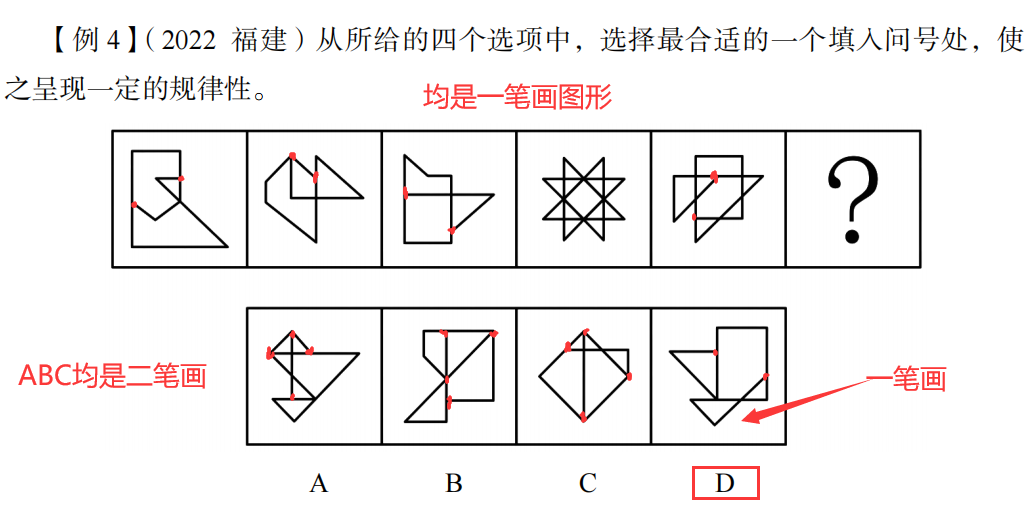
做题技巧:
1.先标出端点——端点必是奇点
2.找“丁”字路口,必是奇点。
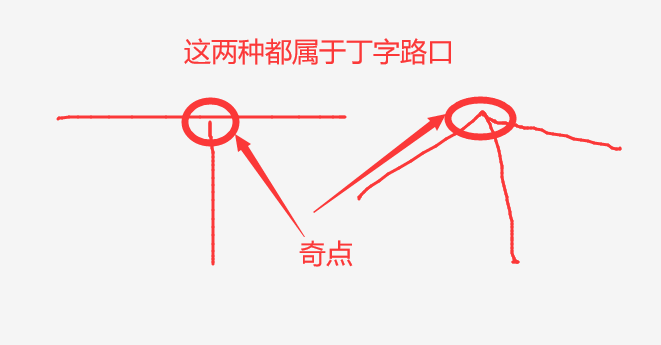

③点数量

什么是“点”?
指线与线的交点,端点不是交点。
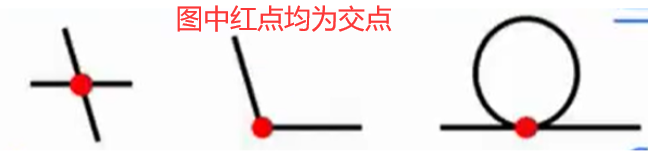
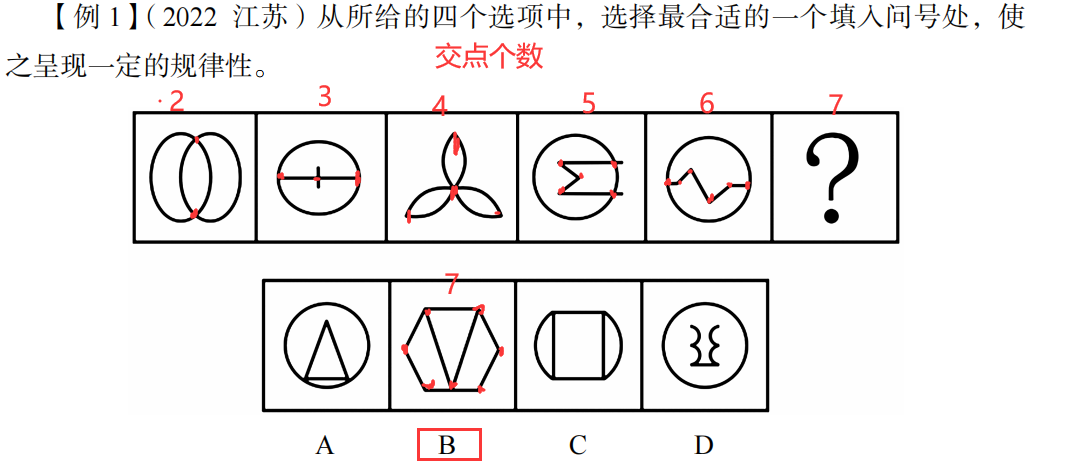
元素组成不同,什么时候数点?
(1)线条之间交叉明显(大树权)
(2)图形相切较多
例题:
补充:
点的细化考法:
1.切点
2.框内外交点
什么时候数切点?
绝大部分图形均出现相切的时候。
例题;
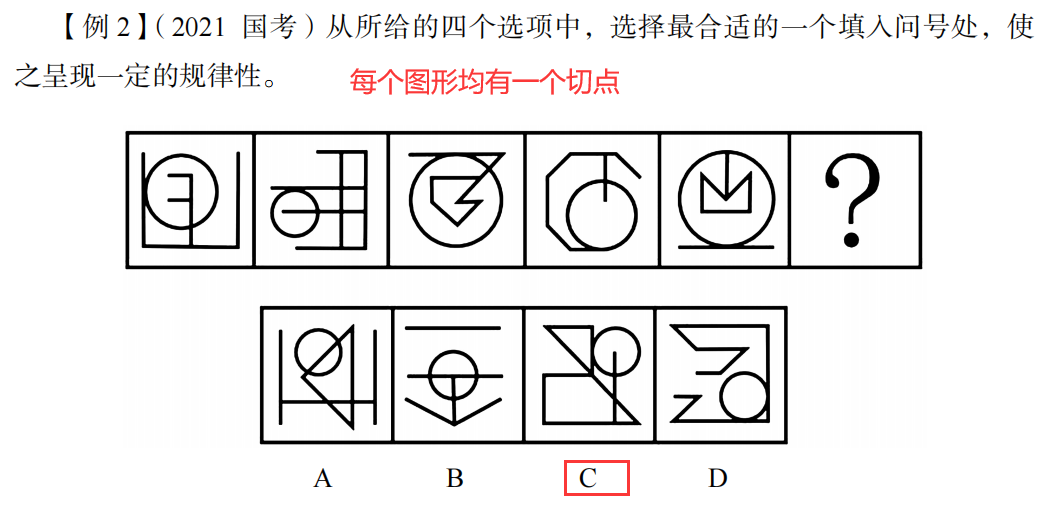
什么时候数框内外交点?
所有图形均出现相同外框时.
例题:
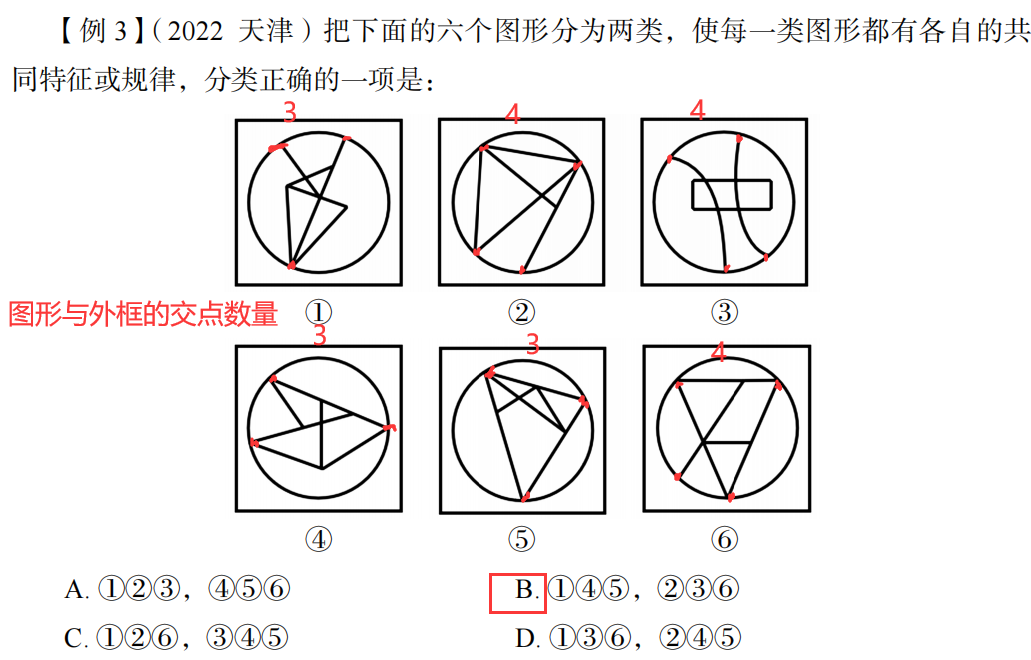
例题;
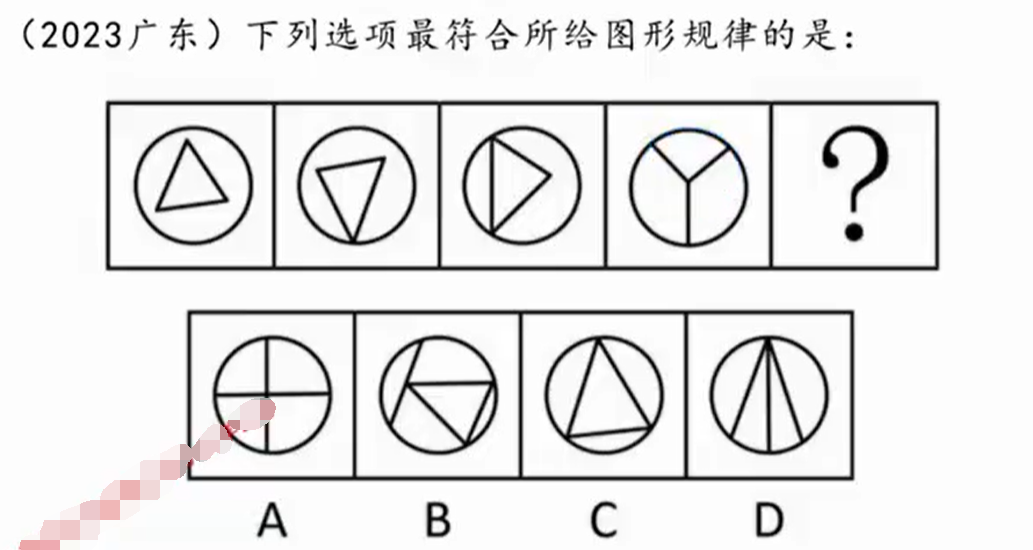
首先看与外框交点,分别是0,1,2,3,问号处为4
再看里面的直线数量,全部都是三条直线
选择D
④素数量



例题:
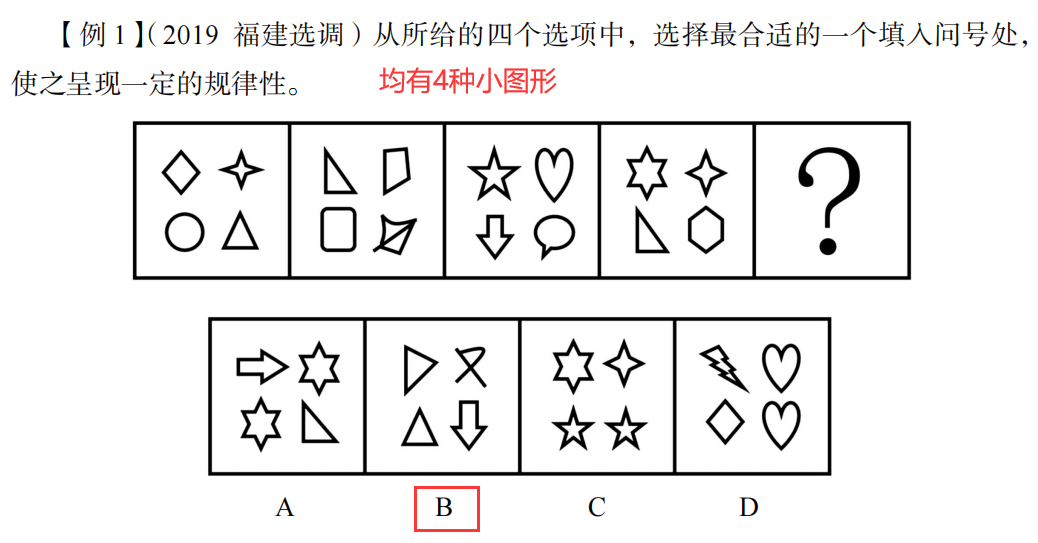

例题;
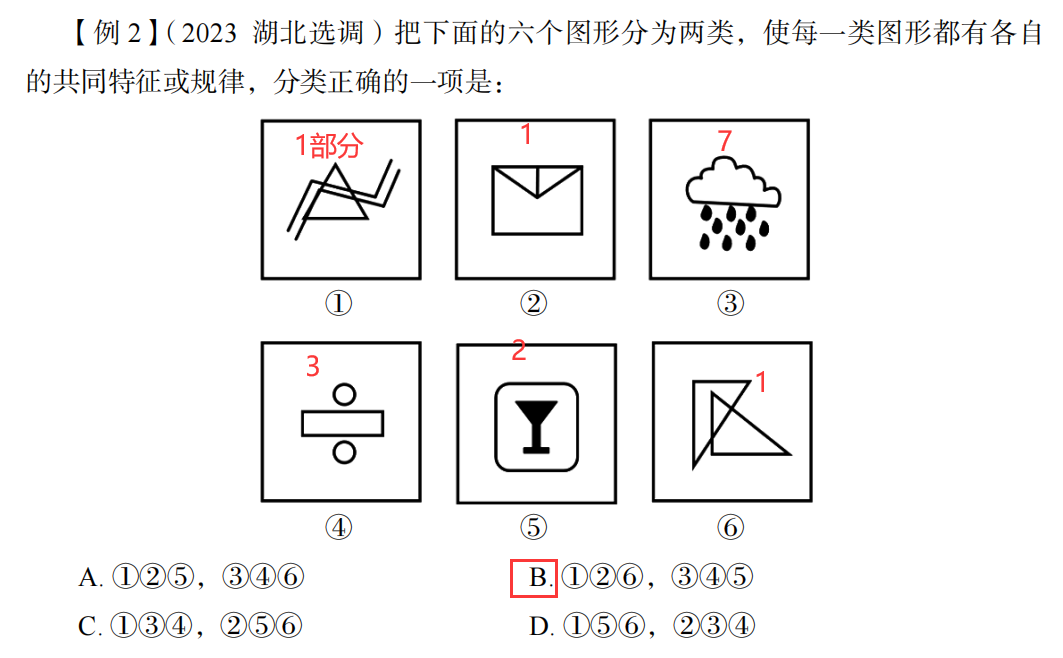
当然这道题也可以用曲线直线来做。
注意:
分类可以是一部分和多部分(常考,别犟,记住就行)
但是不能对称和非对称

(6)空间重构



①相对面
注意:
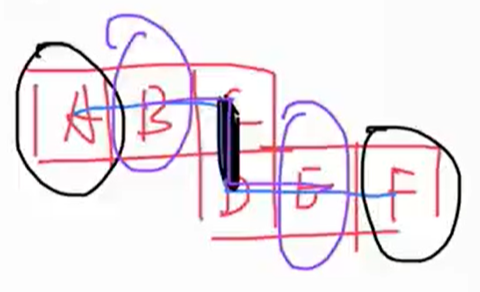
上图中有以A和F为端点的Z字形,但是A和F不是相对面。
B和E才是相对面(B和E在以B和E为端点的Z字形中)。
即Z字形两端且紧靠着“Z”字形中间那条线的才是相对面。
相对面总结
1.什么是相对面?
相对的面。
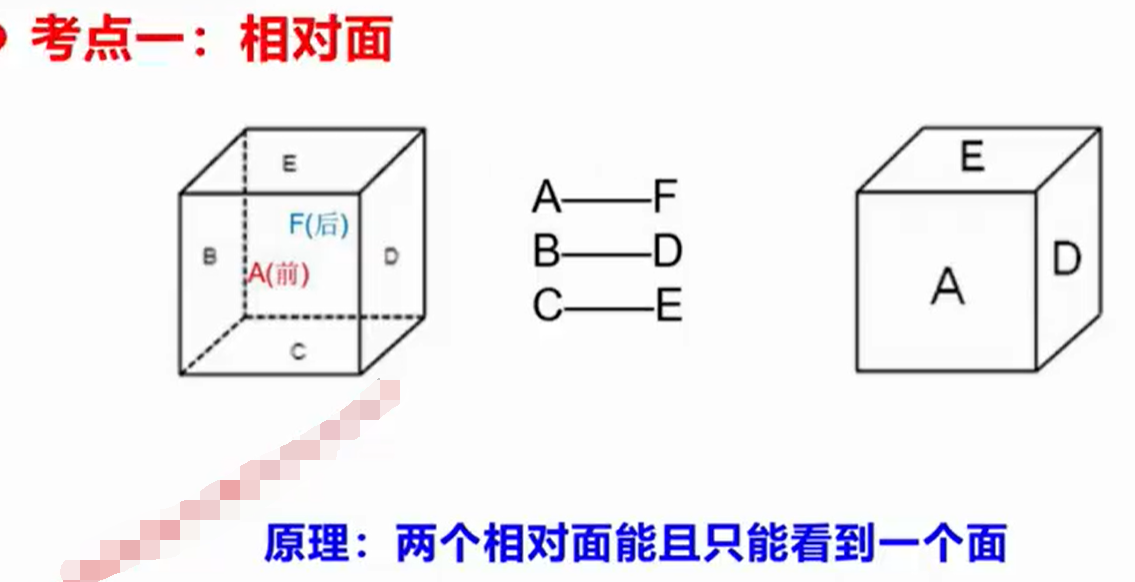
2.相对面的原理:
两个相对面同时能且只能看到一个面。
3.如何判断相对面?
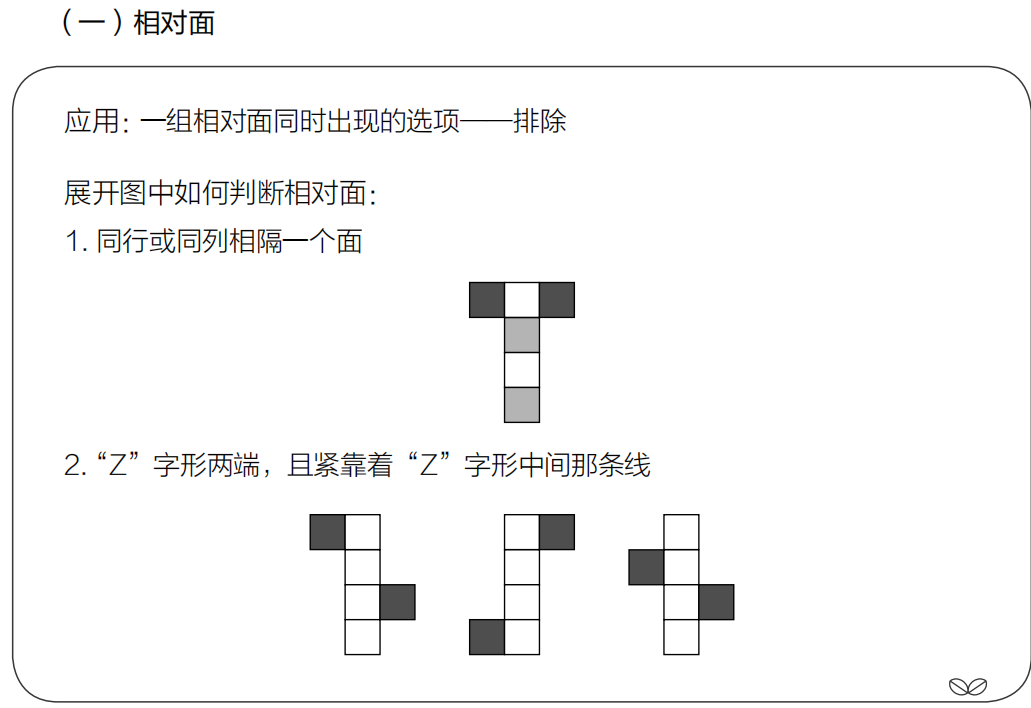
1.同行或同列相隔一个面的两个面互为相对面。
2.Z字形两端且紧靠着“Z”字形中间那条线的两个面互为相对面。
例题;
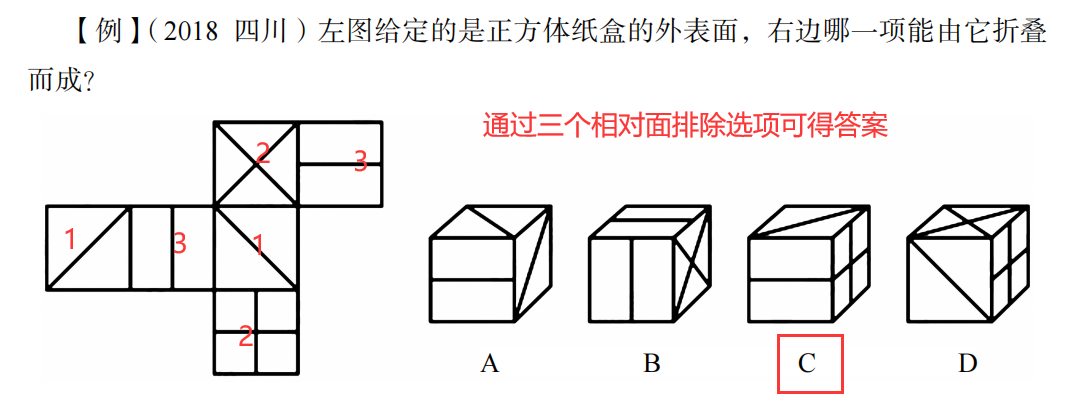
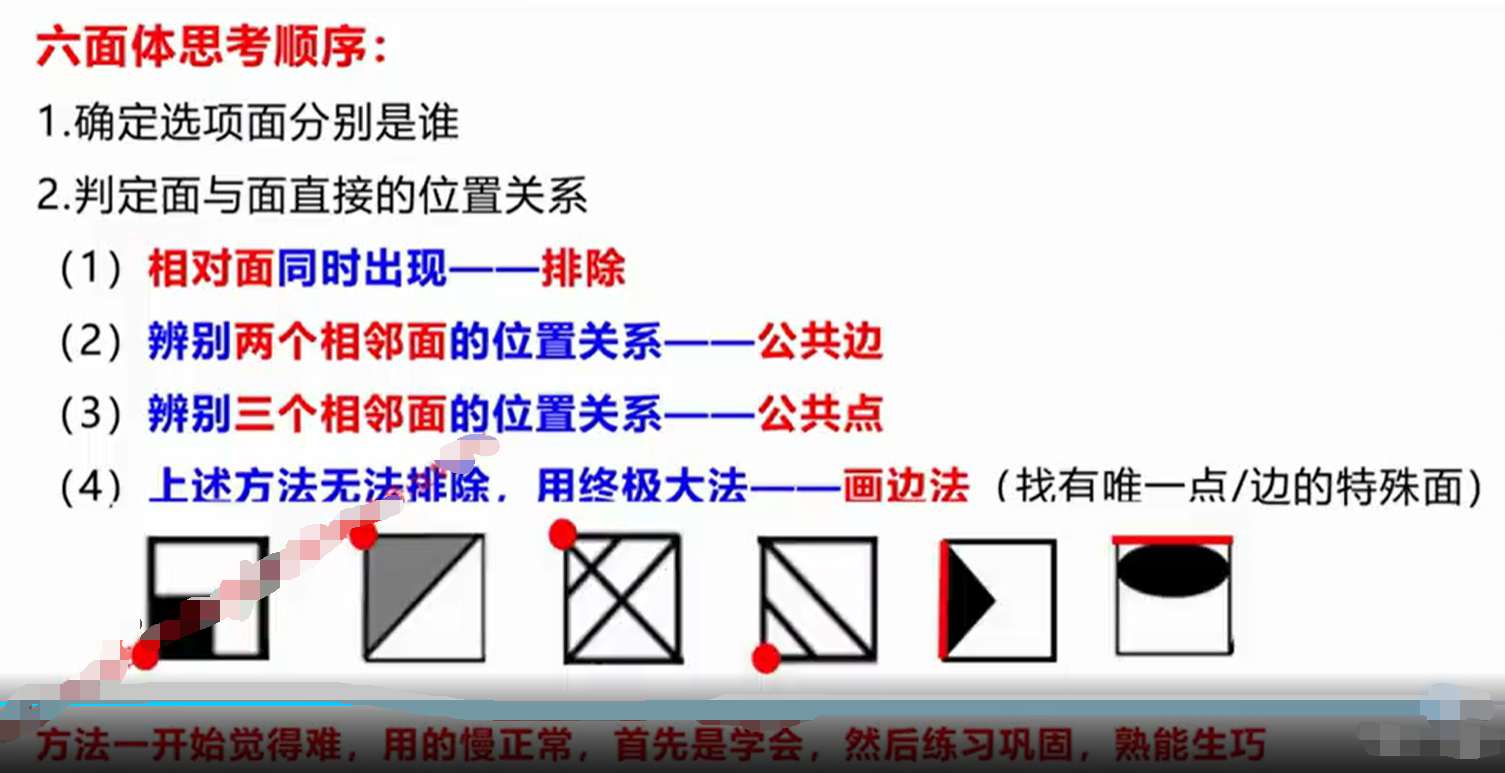
②相邻面
三个考点;
1.公共边。
2.公共点。
3.画边法。
1.公共边:

如何确定公共边?
1.平面图中直接相邻的两个面的公共边
2.平面图中构成直角的两个边是同一条边
3.如果一行/列有4个面,则两头的两条边是同一条边
如下图,同种颜色的是公共边:
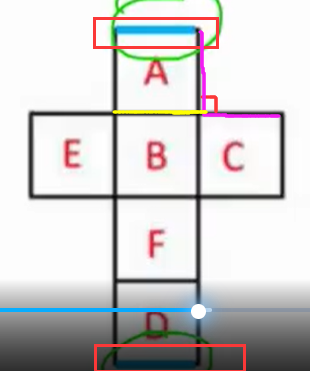
例题:
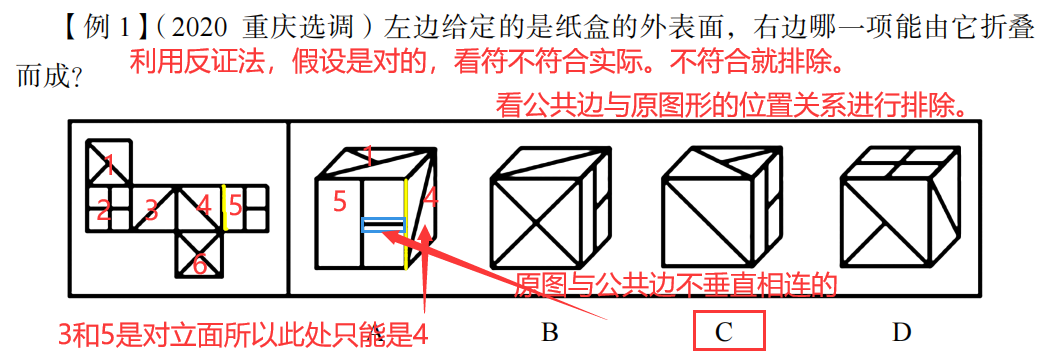
2.公共点:
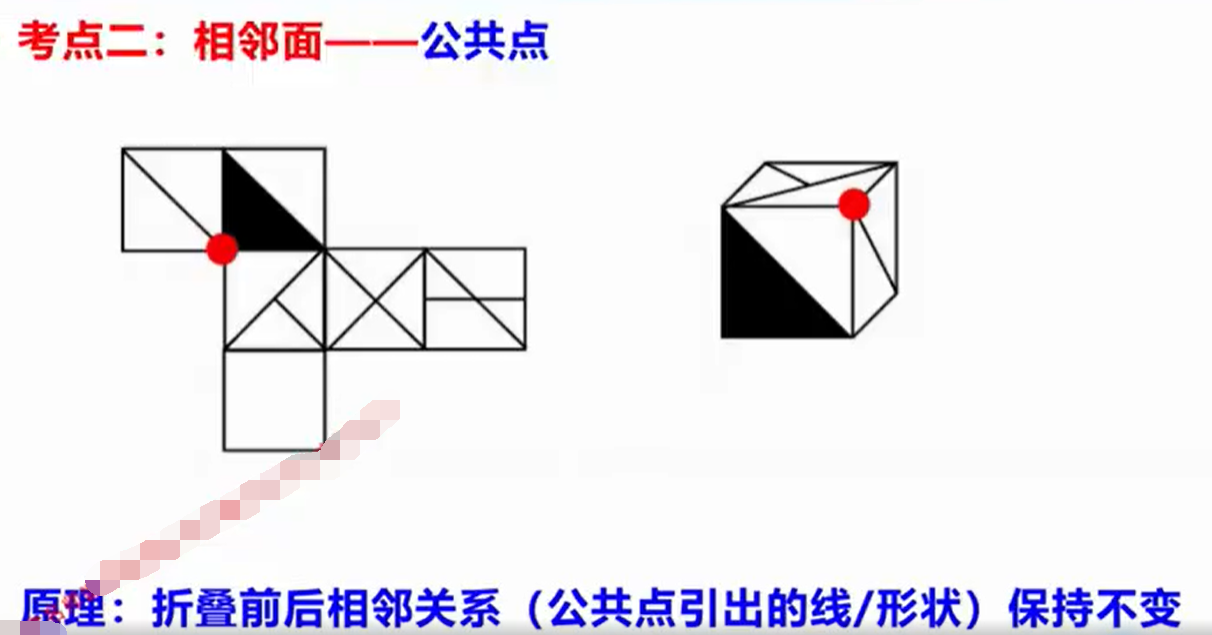
和公共边的思路是一样的,找到公共的点(三个面)然后看相对关系。
例题:
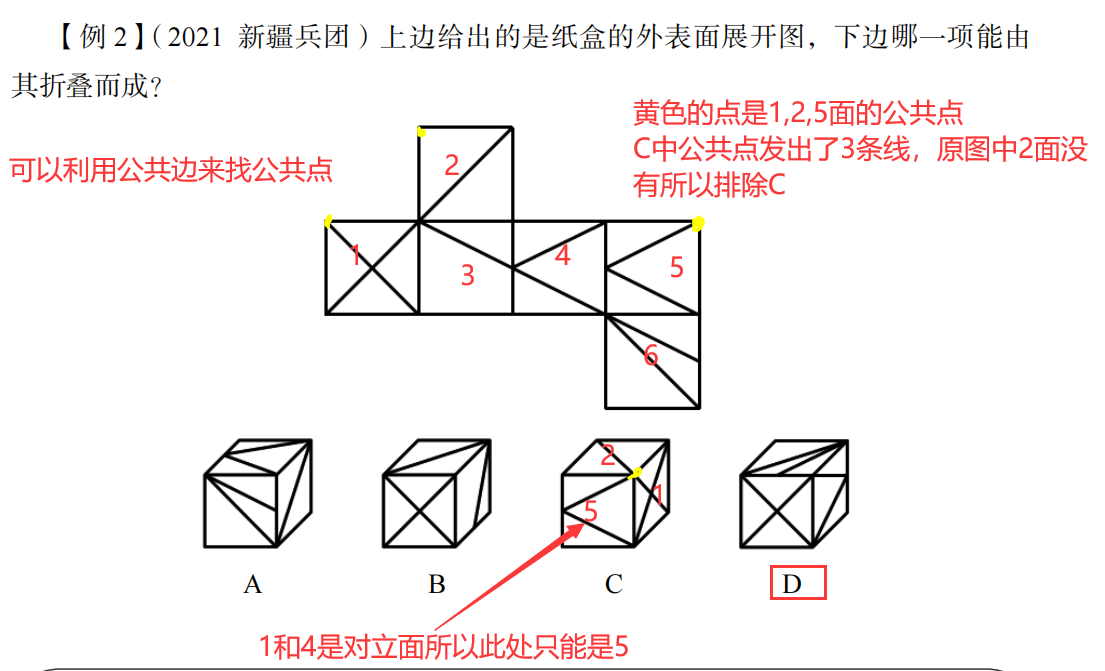
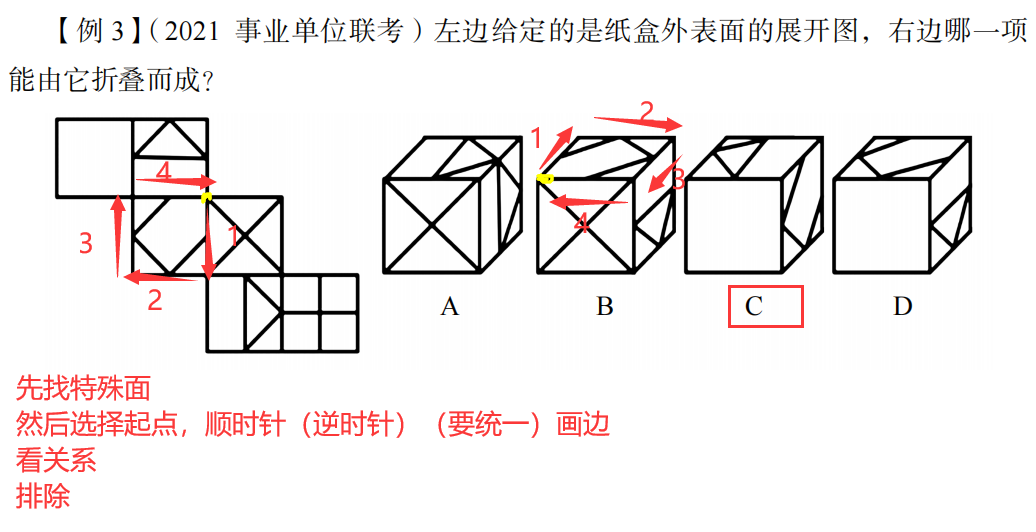
3.画边法:

画边法解题速度不是最快的,但是能解答的题范围设计最大最多的。
什么叫做特殊面?
非中心对称的面
注意:
多个选项都有一个相同的特殊面,可以优先考虑画边法去做。
例题: