数学知识第三期欧拉函数

news2024/11/24 14:33:35

前言

相信大家在高中的时候接触过欧拉函数，希望大家通过本篇文章能够进一步理解欧拉函数！！！

一、什么是欧拉函数？

欧拉函数是一个在数论中用于描述特定正整数的互质数的概念。具体来说，对于一个正整数n，欧拉函数φ(n)表示小于或等于n且与n互质的正整数的数目，包括1本身。换句话说，φ(n)是所有不超过n且与n互素的数的总数。例如，φ(8)表示8与8互质的数，这些数包括1、3、5、7。

欧拉函数的定义可以概括为以下几点：

对于每个正整数n，φ(n)是一个自然数，满足以下条件：
如果n是质数p的k次幂，那么φ(n)可以通过将n乘以质数p的k次方的指数来计算，即φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)；
除了p的倍数之外，其他数都会与n互质；
对于任意两个互质的正整数a和m，有aφ(m) ≡ 1 mod m，这是欧拉定理的一种表述。
此外，欧拉函数具有一些基本的性质，如积性和周期性。积性意味着如果m和n互质，那么φ(mn)等于φ(m)φ(n)。周期性表明φ(n)对于n的奇数值具有重复的模式。

在某些情况下，例如当n是质数p的k次幂时，φ(n)的计算可以通过利用欧拉定理简化。例如，φ(2^3 * 3^2)可以通过计算φ(2^3)和φ(3^2)然后相乘得到24。

综上所述，欧拉函数是一个在数论中非常重要的概念，用于描述和分析互质数的分布规律。

二、例题及模板

1.欧拉函数

模板：

int phi(int x)
{
    int res = x;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1) res = res / x * (x - 1);

    return res;
}

AC代码：

#include <bits/stdc++.h>
using namespace std;

void solve(int n)
{
    int ans = n;
    for (int i = 2; i <= n / i; i ++ )
    {
        if (n % i == 0)
        {
            ans = ans / i * (i - 1);
            while (n % i == 0)  n /= i;
        }
    }
    if (n > 1)  ans = ans / n * (n - 1);
    
    printf("%d\n", ans);
}

int main()
{
    int m;
    scanf("%d", &m);
    while (m -- )
    {
        int x;
        scanf("%d", &x);
        solve(x);
    }
    return 0;
}

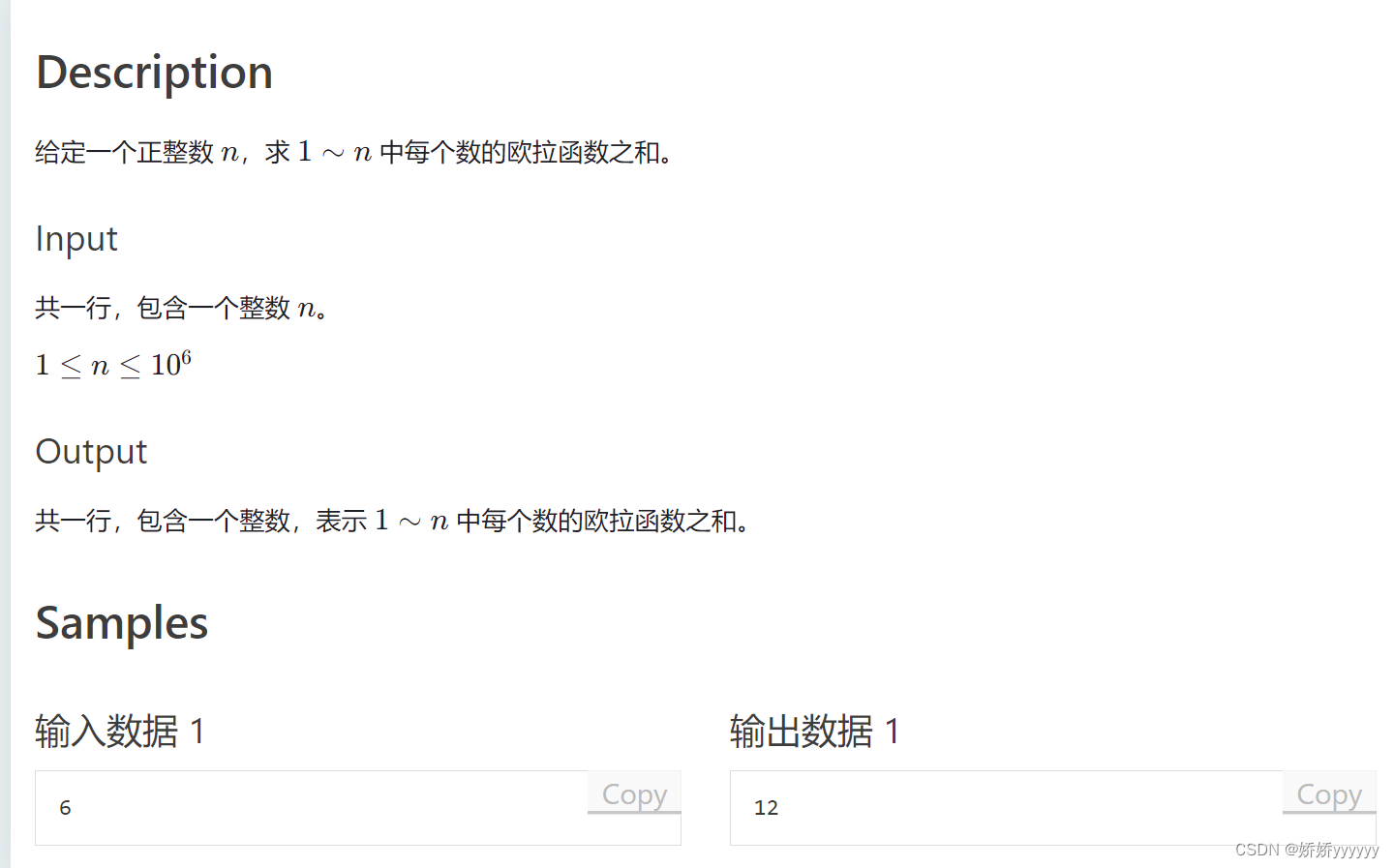
2.筛式法求欧拉函数

模板：

int primes[N], cnt;     // primes[]存储所有素数
int euler[N];           // 存储每个数的欧拉函数
bool st[N];         // st[x]存储x是否被筛掉


void get_eulers(int n)
{
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;
            euler[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0)
            {
                euler[t] = euler[i] * primes[j];
                break;
            }
            euler[t] = euler[i] * (primes[j] - 1);
        }
    }
}

AC代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
using LL = long long ;
int phi[N], primes[N], cnt, n;
bool st[N];

void solve()
{
    phi[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; j < cnt && primes[j] <= n / i; j ++ )
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0)
            {
                phi[i * primes[j]] = phi[i] * primes[j];
                break;
            }
            phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
    
    LL ans = 0;
    for (int i = 1; i <= n; i ++ )  ans += phi[i];
    printf("%lld\n", ans);
}

int main()
{
    scanf("%d", &n);
    solve();
    return 0;
}