算法：

和452. 用最少数量的箭引爆气球 (opens new window)和 435. 无重叠区间 (opens new window)都是一个套路。

这几道题都是判断区间重叠，区别就是判断区间重叠后的逻辑，本题是判断区间重贴后要进行区间合并。

步骤：

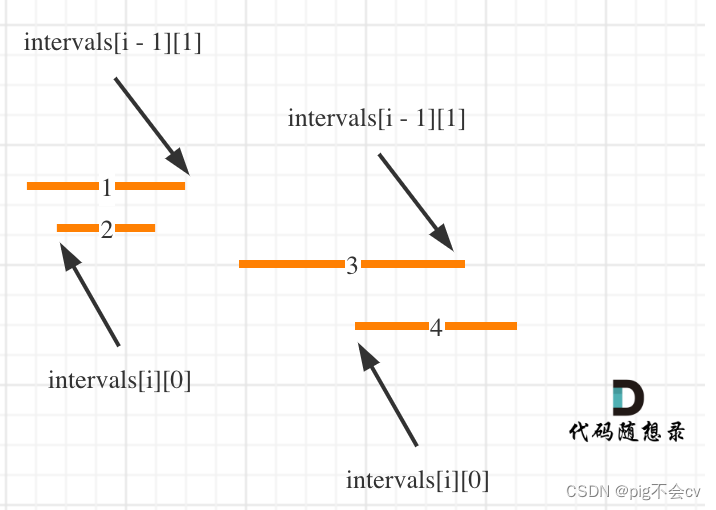
1. 先排序，让所有的相邻区间尽可能的重叠在一起，
2. 按照左边界从小到大排序之后，如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。（本题相邻区间也算重贴，所以是<=）
3. 用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

正确代码：

class Solution {
    public int[][] merge(int[][] intervals) {
        //result初始为链表，方便插入，最后再转为数组int[][]
        List<int[]> result = new LinkedList<>();

        //按左边界升序排序
        Arrays.sort(intervals,(a,b)-> Integer.compare(a[0],b[0]));
        // start和rightbound一定要在排序后赋初值！！！
        //要插入result的新区间的左边界和右边届对应值
        int start = intervals[0][0];
        int rightbound =intervals[0][1];

        /*若intervals[i-1]的右边届大于等于intervals[i]左边届-最大右边届，
        则更新最大右边届为intervals[i]的右边届，合并出一个新的区间*/
        for(int i=1; i<intervals.length; i++){
            if (rightbound >= intervals[i][0]){
                rightbound = Math.max(rightbound, intervals[i][1]);
            }
            else {
         /*若intervals[i-1]的右边届小于intervals[i]左边届，
         则保留原区间，并更新新的区间的左右边界*/
    
                result.add(new int[]{start, rightbound});
                //复制[start, rightbound]区间，加入result
                start = intervals[i][0]; 
                rightbound =intervals[i][1];
            }
            
        }
        result.add(new int[]{start, rightbound});
        return result.toArray(new int[result.size()][]);
    

    }
}

注意：

1.start和rightbound一定要在排序后赋初值！！！

2.result.add(new int[]{start, rightbound});复制[start, rightbound]区间，加入result，不能直接加入

3.在 for 循环外面还有一个`result.add(new int[]{start, rightbound});` 是因为我们需要在循环结束后处理最后一个合并的区间。

如果我们在循环内部添加 `result.add(new int[]{start, rightbound});`，那么当循环结束时，最后一个合并的区间将被忽略。

时间空间复杂度：

时间复杂度 ：

O(NlogN) 排序需要O(NlogN)

空间复杂度 ：

O(logN)  java 的内置排序是快速排序 需要 O(logN)空间