高精度加减乘除算法模板
- 高精度加法算法模板
- 模版题
- 高精度减法算法模板
- 模版题
- 高精度乘法算法模板
- 模版题
- 高精度除法算法模板
- 模版题
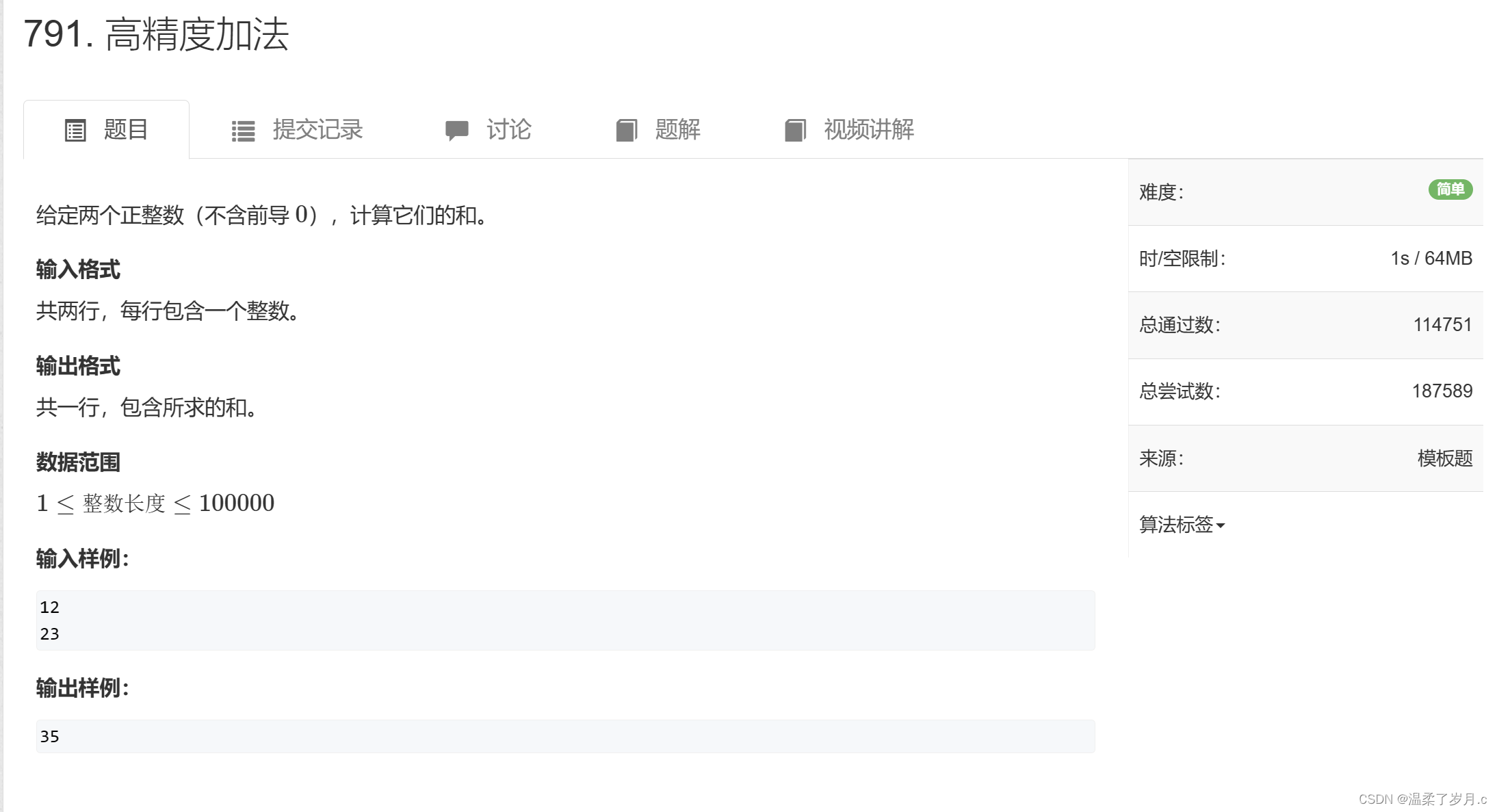
高精度加法算法模板
首先,我们要知道高精度算法是C++才用的,Java中是不需要高精度算法的
高精度加法: 两个大的数相加 (数的范围是 大约为10^6)
这里用vector来做
模版题
#include<vector>
#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
vector<int> add(vector<int> & A, vector<int> & B)
{
vector<int> C;
int t = 0; //表示进位
for(int i = 0; i < A.size() || i < B.size(); i++)
{
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if(t) C.push_back(t); //倒着写,最高位进位的时候方便,直接push_back就行
return C;
}
int main()
{
string str1, str2;
cin >> str1 >> str2;
vector<int> A, B;
for(int i = str1.size() - 1; i >= 0; i--) A.push_back(str1[i] - '0');
for(int i = str2.size() - 1; i >= 0; i--) B.push_back(str2[i] - '0');
auto C = add(A, B);
for(int i = C.size() - 1; i >= 0; i--)
cout << C[i];
cout <<endl;
}
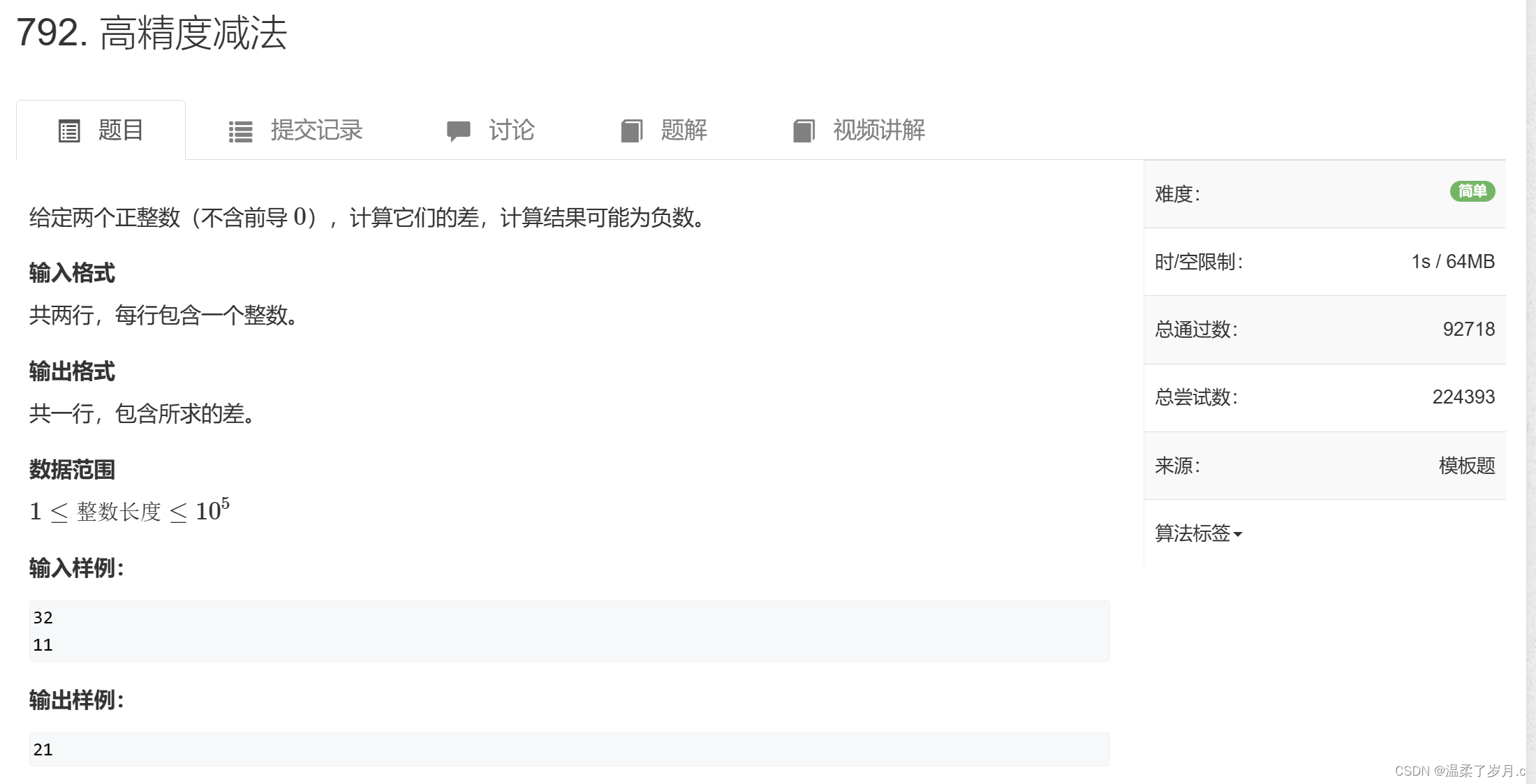
高精度减法算法模板
模版题
#include<iostream>
#include<cstdio>
#include<string>
#include<vector>
using namespace std;
//判断 A,B大小
//如果 A > B, 就A - B, A < B, -(B - A)
bool cmp(vector<int> & A, vector<int> & B)
{
if(A.size() != B.size())
return A.size() > B.size();
for(int i = A.size() - 1; i >= 0; i--)
{
if(A[i] != B[i])
return A[i] > B[i];
}
return true;
}
vector<int> sub(vector<int> & A, vector<int> & B)
{
int t = 0;
vector<int> C;
for(int i = 0; i < A.size(); i++)
{
t = A[i] - t;
if( i < B.size() ) t -= B[i];
C.push_back((t + 10) % 10);
//注意
//:这里 (t + 10) % 10
// 有2种情况:如果t 没有借位,t肯定是大于0的,(t + 10) % 10 为t
// 如果t 需要借位,t肯定是小于0的,t + 10相当于借位了10
//需要借位
if(t < 0) t = 1;
else t = 0; //不需要借位
}
//除去前导0(要注意保留结果为0的情况)
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string str1, str2;
cin >> str1 >> str2;
vector<int> A, B;
for(int i = str1.size() - 1; i >= 0; i--) A.push_back(str1[i] - '0');
for(int i = str2.size() - 1; i >= 0; i--) B.push_back(str2[i] - '0');
if(cmp(A, B))
{
auto C = sub(A, B);
for(int i = C.size() - 1; i >= 0; i--)
{
cout << C[i];
}
}
else
{
auto C = sub(B, A);
cout << "-";
for(int i = C.size() - 1; i >= 0; i--)
{
cout << C[i];
}
}
cout << endl;
return 0;
高精度乘法算法模板
一个大的数(vector存储),乘上一个小的数(int存储)
模版题

//一个大点的数 乘以 一个小点的数(int)
#include<iostream>
#include<cstdio>
#include<vector>
#include<string>
using namespace std;
vector<int> mul(vector<int> & A,int b)
{
vector<int> C;
int t = 0;
// for(int i = 0; i < A.size(); i++)
// {
// t += A[i] * b;
// C.push_back(t % 10);
// t /= 10;
// }
// //处理剩下的t
// while(t)
// {
// C.push_back(t % 10);
// t /= 10;
// }
//合并写
for(int i = 0; i < A.size() || t; i++)
{
if(i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while(C.size() > 1 && C.back() == 0) C.pop_back();
//去掉前导0
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string str1;
int b;
cin >> str1;
cin >> b;
vector<int> A;
for(int i = str1.size() - 1; i >= 0; i--) A.push_back(str1[i] - '0');
auto C = mul(A, b);
for(int i = C.size() - 1; i >= 0; i--) cout << C[i];
cout << endl;
return 0;
}
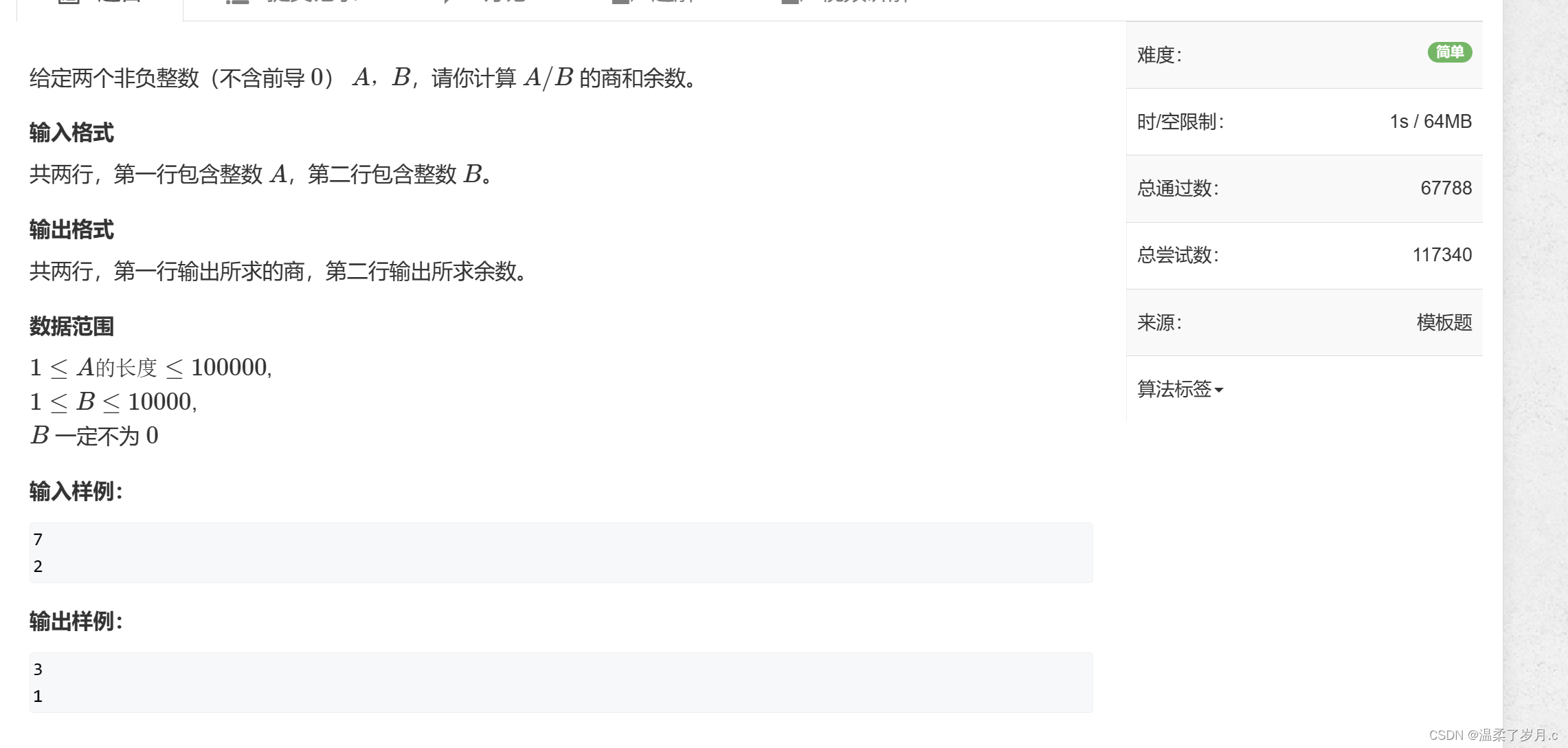
高精度除法算法模板
高精度整数 除上低精度整数
模版题
#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> div(vector<int> & A, int b, int &r)
{
//对A从最高位进行处理
vector<int> C;
for(int i = 0; i < A.size(); i++)
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
//去除前导0, 00在前面,pop_back只能删除后面,所以先反转
reverse(C.begin(), C.end());
while(C.size() > 1 && C.back() == 0)
{
C.pop_back();
}
return C;
}
int main()
{
string str1;
int b;
cin >> str1 >> b;
vector<int> A;
//正着存储的,区别于前三种模版
for(int i = 0; i < str1.size(); i++) A.push_back(str1[i] - '0');
int r = 0;
auto C = div(A, b, r);
for(int i = C.size() - 1; i >= 0; i--) cout << C[i];
cout <<endl;
cout << r;
return 0;
}