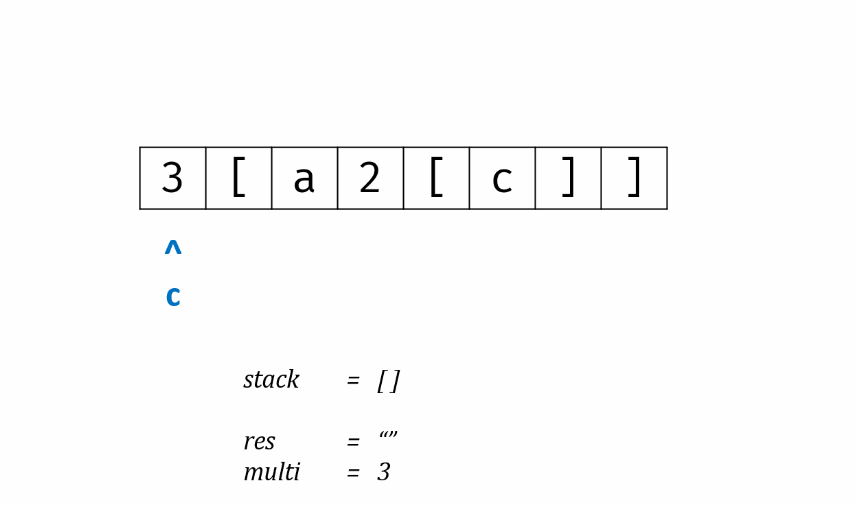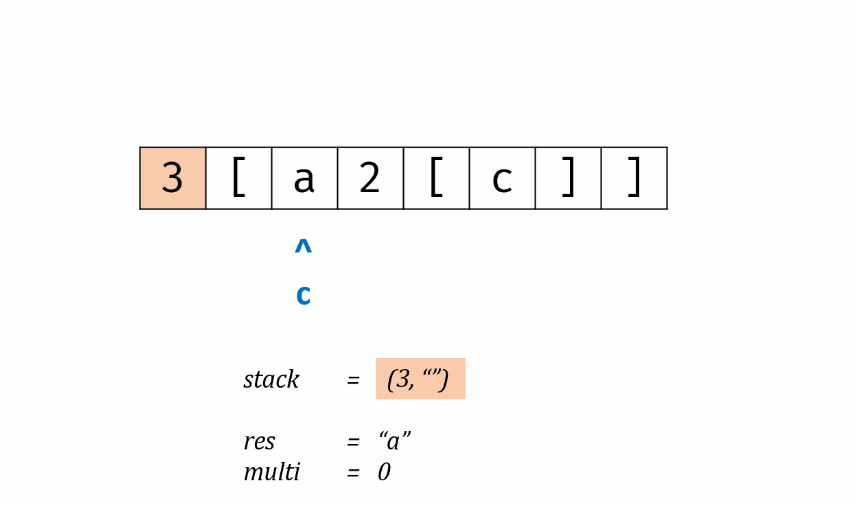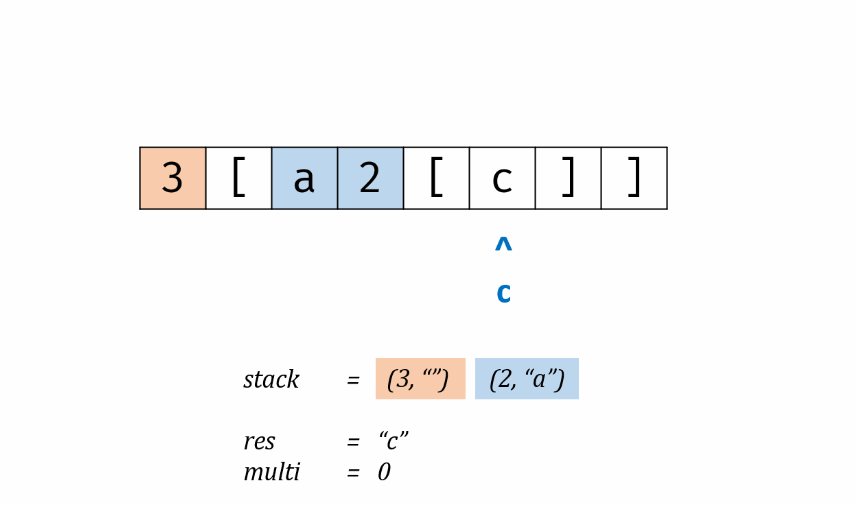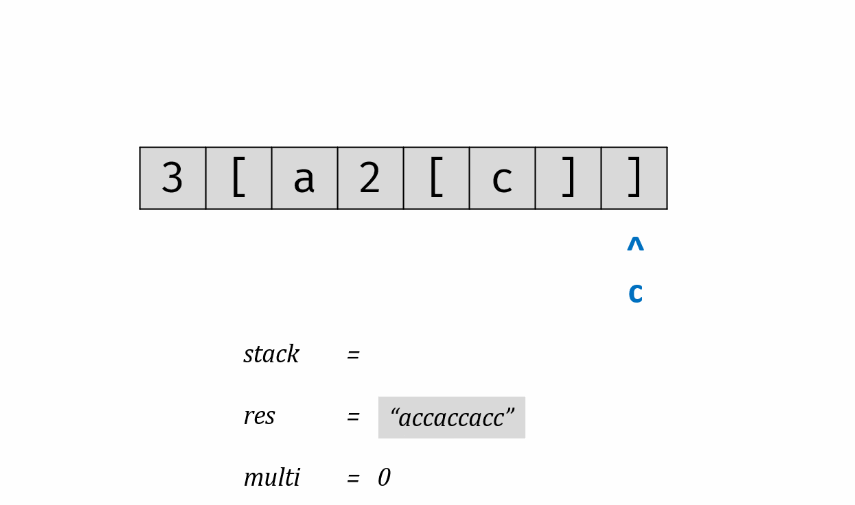主成分分析（PCA）Python

news2024/11/17 7:53:05

实际问题研究中，常常遇到多变量问题，变量越多，问题往往越复杂，且各个变量之间往往有联系。于是，我们想到能不能用较少的新变量代替原本较多的旧变量，且使这些较少的新变量尽可能多地保留原来变量所反映的信息。

比如说一件上衣，有身长、袖长、胸围、腰围等等十多个指标，将型号分这么多很麻烦，因此，厂家将十多项指标综合成3项指标，分别反映长度、胖瘦、特殊体型。

变量具有相关性，同时就意味着反映的信息有重叠性，主成分分析就是将重复的变量（关系紧密的变量）删去，建立尽可能少的、互相无关的新变量。

设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析法，也是数学上用来降维的一种方法。

通过PCA将n维原始特征映射到k维上（k<n），称这k维为主成分。

找新的维度实质上要使数据间的方差够大，即在新维度下坐标点足够分散、数据间有区分。本质上也就是在做基变换。

下图是一个例子，将5个点降维到一条直线上。

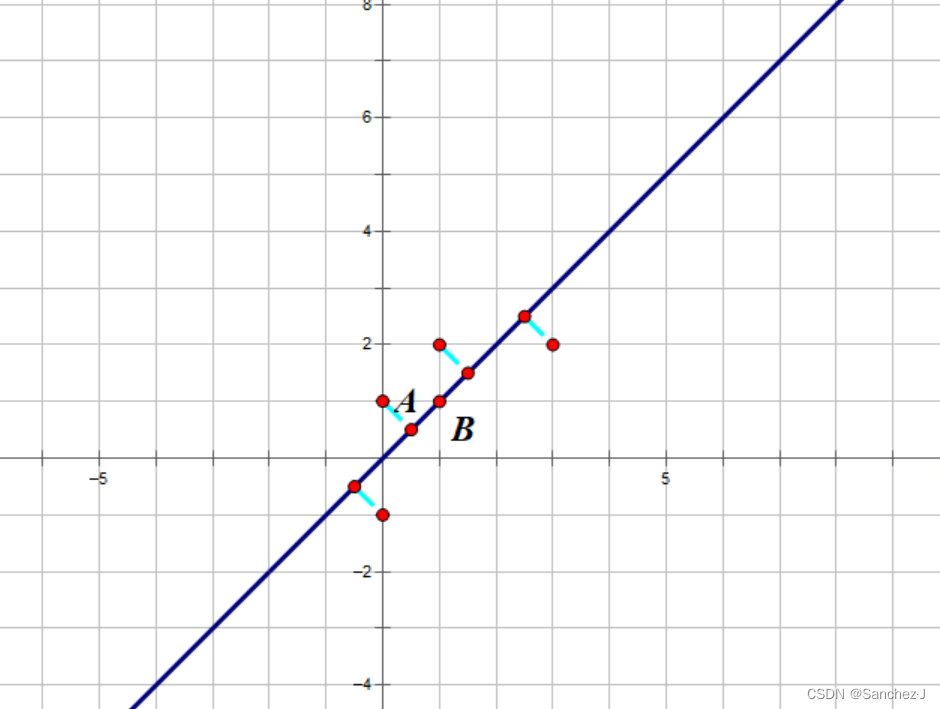
代数上，可以理解为m × n的原始样本X，与n×k阶的矩阵W做矩阵乘法，得到m×k阶低维矩阵Y。

分析思想

假设有n个样板，p个指标，则可以构成大小为n×p的样本矩阵X:

$x=\begin{bmatrix} x_{11} &x_{12} &... &x_{1p} \\ x_{21} &x_{22} & ...& x_{2p} \\ ... &... & ... & ...\\ x_{n1} &x_{n2} &... & x_{np} \end{bmatrix}=(x_1,x_2,...x_p)$

假设我们想找到新的一组变量 $z_1,z_2,...,z_m(m\le p)$ ，其满足

$\left\{\begin{matrix} z_1=l_{11}x_1+l_{12}x_2+...+l_{1p}x_p\\ z_2=l_{21}x_1+l_{22}x_2+...+l_{2p}x_p\\ ...\\ z_m=l_{m1}x_1+l_{m2}x_2+...+l_{mp}x_p \end{matrix}\right.$

系数 $l_{ij}$ 确定原则：

$z_i$ 与 $z_j$ ( $i\neq j;i,j=1,2,...,m$ ) 线性无关
$z_k$ 是 $x_1,x_2,...x_p$ 线性组合中方差第k大者，称原变量指标的第k主成分

PCA计算步骤

标准化处理 $X_{ij}=\frac{x_{ij}-\overline{x_j}}{S_j}$
计算标准化样本的协方差矩阵 $R=\begin{bmatrix} r_{11} &r_{12} &... &r_{1p} \\ r_{21} &r_{22} & ...& r_{2p} \\ ... &... & ... & ...\\ r_{n1} &r_{n2} &... & r_{np} \end{bmatrix}$
计算R的特征值和特征向量（特征值从大到小排序）
计算主成分贡献率以及累计贡献率
贡献率 $\alpha_i=\frac{\lambda_i}{\sum_{k=1}^{p}\lambda_k}(i=1,2,...,p)$
累计贡献率 $\sum G=\frac{\sum_{k-1}^{i}\lambda}{\sum_{k=1}^{p} \lambda_k }(i=1,2,...,p)$
写出主成分：一般取累计贡献率超过80%的特征值所对应的第1，2，...，m个主成分。其中第 i 个是 $F_i=a_{1i}X_1+a_{2i}X_2+...+a_{pi}X_p(i=1,2,...,m)$ （ $a_i$ 是第i个特征向量）
根据系数分析主成分代表的意义

Python代码

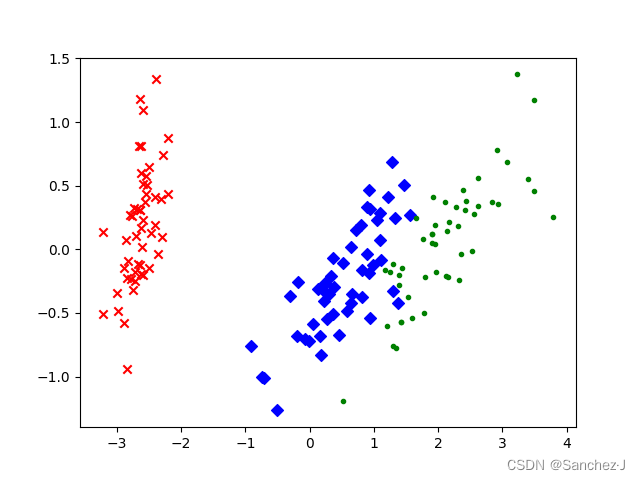
这段代码将Iris数据集降维到二维空间，并使用散点图展示不同类别的鸢尾花在降维后的空间中的分布情况。详见注释。

import matplotlib.pyplot as plt  # 加载matplotlib用于数据的可视化
from sklearn.decomposition import PCA  # 加载PCA算法包
from sklearn.datasets import load_iris  # 从sklearn库中导入load_iris函数，用于加载Iris数据集。

data = load_iris()  # 使用load_iris函数加载Iris数据集。
y = data.target  # 提取数据集的标签（目标变量），表示不同种类的鸢尾花。
x = data.data  # 提取数据集的特征，表示鸢尾花的四个特征。
pca = PCA(n_components=2)  # 加载PCA算法，设置降维后主成分数目为2
reduced_x = pca.fit_transform(x)  # 对原始数据进行PCA降维，将数据转换为新的二维空间。
red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []
#  初始化三个颜色类别（红色、蓝色、绿色）的坐标列表。
for i in range(len(reduced_x)):  # 遍历降维后的数据
    if y[i] == 0:  # 如果数据点属于第一类鸢尾花。
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])
        # 将该点在降维后的第一个主成分的坐标添加到红色类别的x坐标列表中。
        # 将该点在降维后的第二个主成分的坐标添加到红色类别的y坐标列表中。
    elif y[i] == 1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])
    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])
# 可视化
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()

结果