本题中,要求我们求在1-9范围内,满足k个数的和为n的组合(组合是无序的,并且题目中要求不可以重复)。
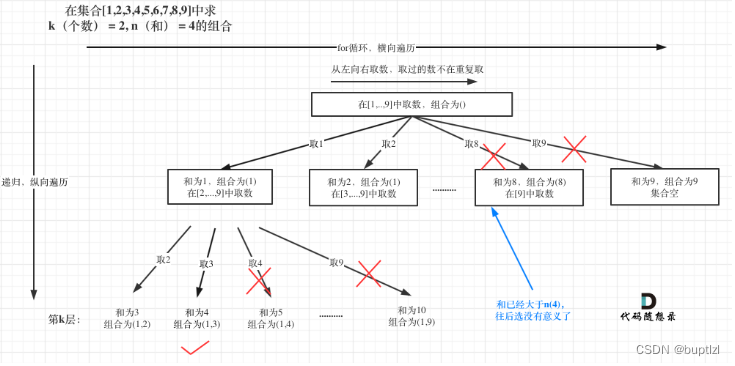
这种组合问题依旧需要用回溯算法来解决。因为我们没办法控制产生k层for循环。回溯算法的过程是构建树结构,树结构的宽度由元素个数来决定,本题中只能取1-9,也就是说树的宽度是9。树的深度,也就是循环的层数由k控制,即我们需要几个数的组合,就需要循环几层,因为每次循环都是取出一个数字!
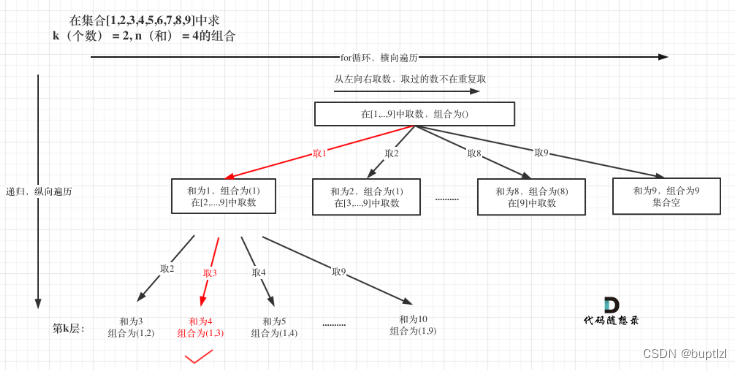
如上图所示,我们的程序整体过程就是这样,但是我们还可以进行剪枝操作。因为如果自己统计的和sum当前已经比target大了,所以我们就没必要再进行下一次递归了,所以这里可以剪枝;应该个地方是控制startIndex,如果我们需要k个数,但当前集合中所剩余的数加上我们已经取出来的数已经不能够满足k个数了,那之后的递归操作也没有必要了,比如k=3,此时如果我们startIndex=8的话,我们只能再取一个9,这确是只有两个数,比k小,不能满足题意!也可以不考虑了。
回溯算法的三部曲与递归类似,可以参考上一题。
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backTracking(n, k, 1, 0);
return result;
}
private void backTracking(int targetSum, int k, int startIndex, int sum) {
// 减枝
if (sum > targetSum) {
return;
}
if (path.size() == k) {
if (sum == targetSum) result.add(new ArrayList<>(path));
return;
}
// 减枝 9 - (k - path.size()) + 1
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
path.add(i);
sum += i;
backTracking(targetSum, k, i + 1, sum);
//回溯
path.removeLast();
//回溯
sum -= i;
}
}
}
思路来源:代码随想录