报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周。
在QQ群上交流答疑:

文章目录
- 1. 动态规划的概念
- 2. 动态规划的两种编码方法
- 3. DP设计基础
- 4. 常见线性DP
- 5. DP习题
第18周: 动态规划初步
动态规划(Dynamic Programming,DP)是Richard Bellman于1950年代发明的应用于多阶段决策的数学方法。和贪心、分治一样,动态规划是一种解题的思路,而不是一个具体的算法知识点。动态规划是地地道道的“计算思维”,非常适合用计算机实现,可以说是独属于计算机学科的计算理论。动态规划是一种需要学习才能获得的思维方法。像贪心、分治这样的方法,在生活中,或在其他学科中有很多类似的例子,很容易联想和理解。但动态规划不是,它是一种生活中没有的抽象计算方法,没有学过的人很难自发产生这种思路。
DP是算法竞赛中最常见的考点之一,蓝桥杯大赛的每一场比赛,每次必有DP题目,少则一题,多则数题。以2023年第十四届蓝桥杯省赛为例,
C/C++:A组“更小的数”、B组“接龙数列”、C组“填充”、研究生组“奇怪的数”。
Java:A组“高塔”、B组“ 数组分割,蜗牛,合并石子”、C组“填充”、研究生组“奇怪的数”。
Python:A组“奇怪的数”、B组“松散子序列,保险箱,树上选点”、C组“填充,奇怪的数”、研究生组“填充,高塔”。
能做DP题目,就有蓝桥杯省赛二等奖的实力。
1. 动态规划的概念
本节以斐波那契数为例说明DP的概念和编程实现。
斐波那契数列是一个递推数列,前几个数是1、1、2、3、5、8,第n个数等于第n-1个和第n-2个相加。斐波那契数的递推公式是:
fib(n) = fib(n-1) + fib(n-2)
斐波那契数列又称为兔子数列。设一对兔子每月能生一对小兔子,小兔子在出生的第一个月没有生殖能力,第二个月便能生育,且所有兔子都不会死亡。从第一对刚出生的兔子开始,问12个月以后会有多少对兔子。
斐波那契数列也常常用楼梯问题来举例。一次可以走一个台阶或者两个台阶,问走到第n个台阶时,一共有多少种走法?要走到第n级台阶,分成两种情况,一种是从n-1级台阶走一步过来,一种是从n-2级台阶走两步过来。这就是斐波那契数列的递推公式。
计算斐波那契数列,可以直接用递推公式计算。这里为了说明动态规划的思想,用递归来求斐波那契数,代码如下。
int fib (int n){
if (n == 1 || n == 2) return 1;
return (fib (n-1) + fib (n-2)); //递归以2的倍数增加
}
为了解决总体问题fib(n),将其分解为两个较小的子问题fib(n-1)和fib(n-2),这就是DP的应用场景。
有一些问题有两个特征:重叠子问题、最优子结构。用DP可以高效率地处理具有这2个特征的问题。
(1)重叠子问题
首先,子问题是原大问题的小版本,计算步骤完全一样;其次,计算大问题的时候,需要多次重复计算小问题。这就是“重叠子问题”。以斐波那契数为例,用递归计算fib(5),分解为图示的子问题。
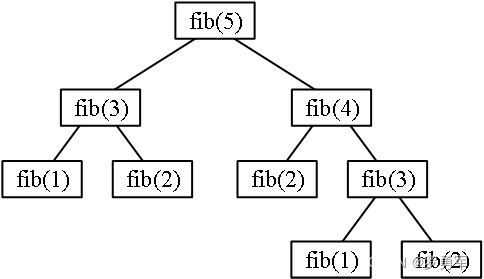
图1 计算斐波那契数
其中fib(3)计算了2次,其实只算1次就够了。
一个子问题的多次重复计算,耗费了大量时间。用DP处理重叠子问题,每个子问题只需要计算一次,从而避免了重复计算,这就是DP效率高的原因。
(2)最优子结构
最优子结构的意思是:首先,大问题的最优解包含小问题的最优解;其次,可以通过小问题的最优解推导出大问题的最优解。在斐波那契问题中,把数列的计算构造成fib(n) = fib(n-1) + fib(n-2),即把原来为n的大问题,减小为n-1和n-2的小问题,这是斐波那契数的最优子结构。
2. 动态规划的两种编码方法
处理DP中的大问题和小问题,有两种思路:自顶向下(Top-Down,先大问题再小问题)、自下而上(Bottom-Up,先小问题再大问题)。
编码实现DP时,自顶向下用带记忆化搜索的递归编码,自下而上用递推编码。两种方法的复杂度是一样的,每个子问题都计算一遍,而且只计算一遍。
(1)自顶向下与记忆化
先考虑大问题,再缩小到小问题,递归很直接地体现了这种思路。为避免递归时重复计算子问题,可以在子问题得到解决时,就保存结果,再次需要这个结果时,直接返回保存的结果就行了。这种存储已经解决的子问题的结果的技术称为“记忆化(Memoization)”。
以斐波那契数为例,记忆化代码如下:
int memoize[N]; //保存结果
int fib (int n){
if (n == 1 || n == 2) return 1;
if(memoize[n] != 0) return memoize[n]; //直接返回保存的结果,不再递归
memoize[n]= fib (n - 1) + fib (n - 2); //递归计算结果,并记忆
return memoize[n];
}
在这个代码中,一个斐波那契数只计算一次,所以总复杂度是O(n)的。
(2)自下而上与制表递推
这种方法与递归的自顶向下相反。这种“自下而上”的方法,先解决子问题,再递推到大问题。通常通过填写表格来完成,编码时用若干for循环语句填表。根据表中的结果,逐步计算出大问题的解决方案。
用制表法计算斐波那契数,维护一个一维表dp[],记录自下而上的计算结果,更大的数是前面两个数的和。

代码:
const int N = 255;
int dp[N];
int fib (int n){
dp[1] = dp[2] =1;
for (int i=3;i<=n;i++) dp[i] = dp[i-1] +dp[i-2];
return dp[n];
}
把表格dp[]称为DP状态,dp[]的转移方程是dp[i] = dp[i-1] +dp[i-2]。
代码的复杂度显然也是O(n)的。
对比“自顶向下”和“自下而上”这两种方法,“自顶向下”的优点是能更宏观地把握问题、认识问题的实质,“自下而上”的优点是编码更直接。两种编码方法都很常见。
能用DP求解的问题,一般是求方案数,或者求最值。
3. DP设计基础
用下面的例子讲解DP的基本问题:状态设计、状态转移、编码实现。
更小的数 2023年第十四届省赛C/C++大学A组,10分
【题目描述】 有一个长度均为n且仅由数字字符0 ~ 9组成的字符串,下标从0到n-1。你可以将其视作是一个具有n位的十进制数字num。小蓝可以从num中选出一段连续的子串并将子串进行反转,最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字numnew满足条件numnew < num。请你帮他计算下一共有多少种不同的子串选择方案。只要两个子串在num中的位置不完全相同我们就视作是不同的方案。注意,我们允许前导零的存在,即数字的最高位可以是0,这是合法的。
【输入描述】输入一行包含一个长度为n的字符串表示num(仅包含数字字符0 ∼9),从左至右下标依次为 0 ∼n−1。对于20%的评测用例,1≤n≤100;对于40%的评测用例,1≤n≤1000;对于所有评测用例,1≤n≤5000。
【输出描述】输出一个整数表示答案。
输入样例:
210102 输出样例:
8
如果读者没学过动态规划,也能用模拟法做这一题。遍历出每个子串,判断这个子串反转后是否合法,也就是判断是否有numnew < num。统计所有合法的情况,就是答案。代码很容易写。
#include<bits/stdc++.h>
using namespace std;
int main() {
string s; cin >> s;
int ans = 0;
for (int i = 0; i < s.size(); i++) {
for (int j = i + 1; j < s.size(); j++) {
string tmp = s;
reverse(tmp.begin()+i, tmp.begin()+j+1); //反转子串s[i,j]
if (tmp < s) ans++;
}
}
cout << ans << endl;
return 0;
}
java代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
int ans = 0;
for (int i = 0; i < s.length(); i++) {
for (int j = i + 1; j < s.length(); j++) {
StringBuilder tmp = new StringBuilder(s);
tmp.replace(i, j + 1, new StringBuilder(s.substring(i, j + 1)).reverse().toString());
if (tmp.toString().compareTo(s) < 0)
ans++;
}
}
System.out.println(ans);
}
}
python
s = input()
ans = 0
for i in range(len(s)):
for j in range(i + 1, len(s)):
tmp = list(s)
tmp[i:j+1] = reversed(tmp[i:j+1])
if ''.join(tmp) < s:
ans += 1
print(ans)
用两种for循环遍历所有的子串。用库函数reverse()反转子串,如果不会用这个函数,也可以自己写一个反转子串的函数。
代码的计算复杂度是多少?两重for循环是
O
(
n
2
)
O(n^2)
O(n2),reverse()是O(n)的,总复杂度为
O
(
n
3
)
O(n^3)
O(n3)。只能通过40%的测试。
下面用DP求解本题,复杂度为
O
(
n
2
)
O(n^2)
O(n2),通过100%的测试。
1、DP状态设计
本题可以用DP吗?它有DP的重叠子问题和最优子结构吗?
在模拟法中,需要检查每个子串,为了应用DP,考虑这些子串之间有没有符合DP要求的关系,请读者思考。下面的DP状态设计和DP转移方程体现了子串之间的DP关系。
DP状态:定义二维数组dp[][],dp[i][j]表示子串s[i]~s[j]反转之后是否大于反转前的子串。dp[i][j]=1表示反转之后变小,符合要求;dp[i][j]=0表示反转之后没有变小。
在DP题目中,建议把状态命名为dp,这有利于与队友的交流。队友看到dp这个关键字,用不着解释,就知道这是一道DP题,dp是定义的状态,而不是别的意思。
2、DP转移方程
对于每个子串,比较它的首尾字符s[i]和s[j],得到状态转移方程。
(1)若s[i] > s[j],说明反转后的子串肯定小于原子串,符合要求,赋值dp[i][j] = 1。
(2)若s[i] < s[j],说明反转后的子串肯定大于原子串,赋值dp[i][j] = 0。
(3)若s[i] = s[j],需要继续比较s[i+1]和s[j-1],有dp[i][j] = dp[i+1][j-1]。
第(3)条的dp[i][j] = dp[i+1][j-1]是自顶向下的思路,例如dp[1][6] = dp[2][5],dp[2][5] = dp[3][4],等等。
计算这个递推公式时,需要先算出较小子串的dp[][],再递推到较大子串的dp[][]。例如先要计算出dp[2][5],才能递推到dp[1][6]。最小子串的dp[][],例如dp[1][1]、dp[1][2]、dp[2][2]、dp[2][3]等,它们不再需要递推,因为dp[1][1]=0,dp[1][2]根据(1)、(2)计算。
3、代码
根据上述思路,读者可能很快就写出了以下代码。
#include<bits/stdc++.h>
using namespace std;
int dp[5010][5010];
int main() {
string s; cin >> s;
int ans = 0;
for (int i = 0; i < s.length(); i++) { //子串从s[i]开始
for (int j = i+1; j < s.length(); j++) { //子串末尾是s[j]
if (s[i] > s[j]) dp[i][j] = 1;
if (s[i] < s[j]) dp[i][j] = 0;
if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1];
if (dp[i][j] == 1) ans++;
}
}
cout << ans;
}
代码的计算复杂度:两重for循环
O
(
n
2
)
O(n^2)
O(n2),优于前面模拟法代码的
O
(
n
3
)
O(n^3)
O(n3)。
代码看起来逻辑很清晰,但它其实是错误的。问题出在第7、8行的for循环。例如第7行i=0,第8行j=8时,递推得dp[0][8]=dp[1][7],但是此时dp[1][7]已经计算过吗?并没有。
递推的时候,根据DP的原理,应该先算出小规模问题的解,再递推大规模问题的解。计算应该这样进行:
(1)初始化:dp[][]=0,其中的dp[0][0]=0、dp[1][1]=0、…、dp[1][0]、…,在后续计算中有用。
(2)第一轮递推:计算长度为2的子串的dp[][],即计算出dp[0][1]、dp[1][2]、dp[2][3]、…。例如计算dp[0][1],若s0>s1,则dp[0][1]=1;若s0<s1,则dp[0][1]=0;若s0=s1,则dp[0][1]=dp[1][0]=0,这里dp[1][0]=0是初始化得到的。
(3)第二轮递推:计算长度为3的子串的dp[][],即计算出dp[0][2]、dp[1][3]、dp[2][4]、…。例如计算dp[0][2],若s0=s2,则有dp[0][2]=dp[1][1]=0,这时用到了前面得到的dp[1][1]。
(4)第三轮递推:计算长度为4的子串的dp[][],即计算出dp[0][3]、dp[1][4]、dp[2][5]、…。例如计算dp[0][3],若s0=s3,则有dp[0][3]=dp[1][2],这时用到了前面得到的dp[1][2]。
(5)继续递推,最后得到所有的dp[][]。
代码应该这样写,用循环变量k表示第k轮递推,或者表示递推长度为k+1的子串:
C++代码:
#include<bits/stdc++.h>
using namespace std;
int dp[5010][5010]; //全局数组,初始化为0
int main() {
string s; cin >> s;
int ans = 0;
for (int k = 1; k < s.length(); k++) { //第k轮递推。k=j-i
for (int i = 0; i+k < s.length(); i++) { //子串从s[i]开始
int j = i+k; //子串末尾是s[j]
if (s[i] > s[j]) dp[i][j] = 1;
if (s[i] < s[j]) dp[i][j] = 0;
if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1];
if (dp[i][j] == 1) ans++;
}
}
cout << ans;
}
java代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
int[][] dp = new int[5010][5010];
int ans = 0;
for (int k = 1; k < s.length(); k++) {
for (int i = 0; i + k < s.length(); i++) {
int j = i + k;
if (s.charAt(i) > s.charAt(j)) dp[i][j] = 1;
if (s.charAt(i) < s.charAt(j)) dp[i][j] = 0;
if (s.charAt(i) == s.charAt(j))dp[i][j] = dp[i + 1][j - 1];
if (dp[i][j] == 1) ans++;
}
}
System.out.println(ans);
}
}
python代码
s = input()
dp = [[0] * 5010 for _ in range(5010)]
ans = 0
for k in range(1, len(s)):
for i in range(len(s) - k):
j = i + k
if s[i] > s[j]: dp[i][j] = 1
if s[i] < s[j]: dp[i][j] = 0
if s[i] == s[j]: dp[i][j] = dp[i + 1][j - 1]
if dp[i][j] == 1: ans += 1
print(ans)
4、对比DP代码和模拟代码
DP代码和模拟代码的相同处:它们都需要计算所有的子串,共
O
(
n
2
)
O(n^2)
O(n2)个子串。
为什么DP代码的效率更高呢?
(1)模拟代码对每个子串的计算是独立的。每个子串的计算和其他子串无关,不用其他子串的计算结果,自己的计算结果对其他子串的计算也没有用。每个子串需要计算O(n)次,
O
(
n
2
)
O(n^2)
O(n2)个子串的总计算量是
O
(
n
3
)
O(n^3)
O(n3)的。
(2)DP的子串计算是相关的。长度为2的子串计算结果,在计算长度为3的子串时用到;长度为3的子串计算结果,在计算长度为4的子串时用到;…等等。所以一个子串的计算量只有O(1),
O
(
n
2
)
O(n^2)
O(n2)个子串的总计算量是
O
(
n
2
)
O(n^2)
O(n2)的。这就是DP利用“重叠子问题”得到的计算优化。
4. 常见线性DP
线性DP是蓝桥杯省赛最常考核的题型。
本博客写过类似的博文,请参考:DP概述和常见DP面试题
非线性DP,蓝桥杯省赛可能考到的有:树形DP、状态压缩DP、数位DP。这属于较难的知识了,初学者以后再学。见专辑:DP专题
5. DP习题
2023年第14届省赛的DP题很多,大多是线性DP,大家可以作为练习题:
C/C++:A组“更小的数”、B组“接龙数列”、C组“填充”、研究生组“奇怪的数”。
Java:A组“高塔”、B组“ 数组分割,蜗牛,合并石子”、C组“填充”、研究生组“奇怪的数”。
Python:A组“奇怪的数”、B组“松散子序列,保险箱,树上选点”、C组“填充,奇怪的数”、研究生组“填充,高塔”。