题目
北极的某区域共有 n 座村庄,每座村庄的坐标用一对整数 (x,y) 表示。
为了加强联系,决定在村庄之间建立通讯网络,使每两座村庄之间都可以直接或间接通讯。
通讯工具可以是无线电收发机,也可以是卫星设备。
无线电收发机有多种不同型号,不同型号的无线电收发机有一个不同的参数 d,两座村庄之间的距离如果不超过 d,就可以用该型号的无线电收发机直接通讯,d 值越大的型号价格越贵。现在要先选择某一种型号的无线电收发机,然后统一给所有村庄配备,数量不限,但型号都是 相同的。
配备卫星设备的两座村庄无论相距多远都可以直接通讯,但卫星设备是 有限的,只能给一部分村庄配备。
现在有 k 台卫星设备,请你编一个程序,计算出应该如何分配这 k 台卫星设备,才能使所配备的无线电收发机的 d 值最小。
例如,对于下面三座村庄:
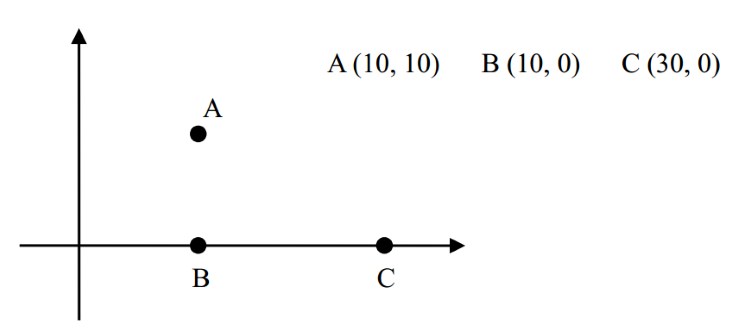
其中,|AB|=10,|BC|=20,|AC|≈22.36。
如果没有任何卫星设备或只有 1 台卫星设备 (k=0 或 k=1),则满足条件的最小的 d=20,因为 A 和 B,B 和 C 可以用无线电直接通讯;而 A 和 C 可以用 B 中转实现间接通讯 (即消息从 A 传到 B,再从 B 传到 C);
如果有 2 台卫星设备 (k=2),则可以把这两台设备分别分配给 B 和 C ,这样最小的 d 可取 10,因为 A 和 B 之间可以用无线电直接通讯;B 和 C 之间可以用卫星直接通讯;A 和 C 可以用 B 中转实现间接通讯。
如果有 3 台卫星设备,则 A,B,C 两两之间都可以直接用卫星通讯,最小的 d 可取 0。
输入格式
第一行为由空格隔开的两个整数 n,k;
接下来 n 行,每行两个整数,第 i 行的 xi,yi 表示第 i 座村庄的坐标 (xi,yi)。
输出格式
一个实数,表示最小的 d 值,结果保留 2 位小数。
数据范围
1≤n≤500
0≤x,y≤104
0≤k≤100
输入样例:
3 2
10 10
10 0
30 0
输出样例:
10.00思路
使用kruskal算法生成k个团,将这k个团使用卫星进行连接。
使用kruskal算法生成k个团的时候,是生成了k个最小生成树,取出这k个团中的最长边,即为答案。
代码
#include<bits/stdc++.h>
using namespace std;
typedef pair<double,pair<int,int>> PII;
const int N = 510;
int n,k;
int p[N];
priority_queue<PII,vector<PII>,greater<>> heap;
struct eg{
int x,y;
}e[N];
double get_dist(int xx1,int yy1,int xx2,int yy2)
{
int dx = abs(xx1 - xx2);
int dy = abs(yy1 - yy2);
return sqrt(dx * dx + dy * dy);
}
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> k;
for(int i = 1; i <= n; i ++) p[i] = i;
for(int i = 1; i <= n; i ++) cin >> e[i].x >> e[i].y;
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= n; j ++)
{
heap.push({get_dist(e[i].x,e[i].y,e[j].x,e[j].y),{i,j}});
}
}
int cnt = n;
double ans = 0;
while(!heap.empty())
{
if(cnt <= k) break;
auto t = heap.top();
heap.pop();
int x = find(t.second.first);
int y = find(t.second.second);
double dist = t.first;
if(x == y) continue;
ans = dist;
cnt --;
p[x] = y;
}
printf("%.2f",ans);
return 0;
}
| 难度:中等 |
| 时/空限制:1s / 64MB |
| 总通过数:5332 |
| 总尝试数:12887 |
| 来源:《信息学奥赛一本通》 , Waterloo University 2002 |
| 算法标签 最小生成树Kruskal |
题目来自: 1145. 北极通讯网络 - AcWing题库