一、fraud

跑了一个lr模型，从正则，一直看到了极大似然和最大后验估计emmm。一路跑偏，已经0954了。先把实验结果抄一抄

本来想把模型都跑完，没想到看R补充了大量的基本知识（L1\L2正则、先验概率

今天先来看fraud
看的时候，要知道原来模型的大体内容，效果，改进空间。

下午场开始啦~1351。
再花一个小时总结一下APT论文，然后和老师汇报。

二、APT

完美用了一个小时看完、总结完了paper，并push了一下老师。休息了一下，打算再看看上午学的内容。

最近开始用markdown了，感觉还蛮爽的！
呜呜呜，刚刚看csdn私信，发现被夸了，好开心啊！！！

三、基础模型与LR相关内容总结（上午内容）

（一）正则化方法

1、L1,L2

正则化，约束了解空间。
L1正则化用参数绝对值约束，看起来像是个有棱角的方形。不易求导，更容易为0，更加稀疏，很多参数最后为0。
L2正则化用参数欧氏距离约束，是圆形约束。

在这里插入图片描述

（二）极大似然估计

这是一个谜一样的存在，当时再看《统计学习方法》的时候就因为这个一度放弃，今天终于可以弄明白一点了！！

1、似然函数

所谓似然函数，其实就是我们熟悉的概率函数P(X|θ)的另一种解读方法。
(1)如果模型参数θ已知，x为变量，那么求不同x出现的可能性就是我们平时说的概率函数
(2)如果x已知，而θ为变量，那么对于不同的θ，导致出现x的概率，则为似然函数。也就是，对于不同的θ，出现已知x的可能性。

2、极大似然估计

MLE:most likelihood estimate
一般x是已知的，由我们抽样获取的，我们希望通过抽样实验估计出模型参数θ的值。
于是，我们求解，在θ为什么值的时候，最可能出现我们抽样出的结果，认为该θ为模型的最优值。这里面包含了一层意思——我们认为我们抽样的结果可以反应数据本身的分布，即我们根据我们的样本，估计了一个使模型生成该样本数据的最佳参数。我们无比相信我们的抽样结果x。

3、最大后验估计

MAP:Maximum A Posteriori
在考虑极大似然估计的时候，我们只考虑了什么样的θ可以让x最大可能出现，但是并没有考虑theta本身出现的概率，所以并不能反映P（θ|x），也就是已知x，某个theta真正出现的概率，即最大后验估计。这也是贝叶斯学派的思想，强调加入先验概率P（θ）

4、MLE和MAP

个人感觉，
MLE是无比相信某一次实验的结果，仅仅看实验结果，求θ，使得实验结果最大可能出现；
而MAP，则是在MLE的基础上做了一些correction，类似于补了一刀，虽然这个θ可以使本次实验结果最大可能出现，但是有可能这个θ本身的出现并不符合常理，要用P(θ)纠正。

所以，二者之间，其实可以通过实验次数来不断靠近——实验次数多了，那么一次实验的结果也就有说服力了，靠近真实结果了，MLE也就不会被P（θ）影响太多了，因为常识其实已经在不断的实验中被注入了。

从数学上讲，例如，投硬币实验，实验次数多了，那么θ次方也就多了，最大值就不会轻易被P(θ)的分布带跑偏了。

当然，如果有顽固贝叶斯学派，认为θ日常只可能出现在0.5，即P（θ=0.5）=1，那么无论怎样，MAP只能为theta=0.5，在取其他值的时候，P（θ|x）=0，也就是知识注入太强势了。

（三）不同的avg

A. Micro考虑所有样本，直接算

B. Macro先针对不同类别算，再在类别之间直接平均

C. weighted针对不同类别算后，加权求平均

（四）LR原理

兜兜转转，回到最初的起点。
其实感觉逻辑回归就是个模型嘛~这个模型其实就是线性+sigmoid拟合。

1、预测函数

其中z其实就是θT·x的线性组合，h（x）求出来在0~1，我们为其赋予意义：y为1的可能性。
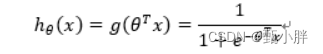
在这里插入图片描述

在这里插入图片描述

2、损失函数Loss

由于定义了h（x）的含义：y为1的可能性，那么就可以据此分类讨论，Yt为0和1的情况啦。
如果Yt=0，我希望预测结果也为0，则结果越靠近0，损失越小，越靠近1，损失越大，于是L（h（x），y）=-log（1-h（x））；
如果Yt=1，则希望预测结果也越靠近1，结果越靠近1，损失越小，则L（h(x),y）=-log（h（x）），这里采用-log作为代价函数
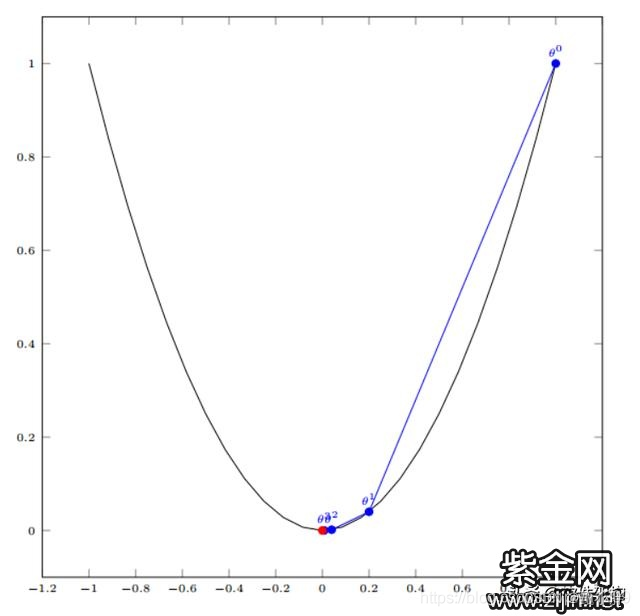
在这里插入图片描述