投标价格重预算
背景
甲方需要采购一批物资,采购数量为甲方给定的预计采购数量,并限制了采购总价。例甲方采购预算清单如下,采购总预算为不超过 3175 元
| 采购内容 | 采购数量 | 投标单价 | 投标报价合计 |
| 电脑 | 10 | ||
| 空调 | 20 | ||
| 洗衣机 | 8 | ||
| 桌子 | 7 | ||
| 打印机 | 35 | ||
| 合计 | |||
注:乙方根据以上预算清单填报单价,最终数量按实结算,单价不变
我方竞标时在甲方预算清单内填报单价,假设我方报价如下:
| 采购内容 | 采购数量 | 投标单价 | 投标报价合计 |
| 电脑 | 10 | 15 | 150 |
| 空调 | 20 | 20 | 400 |
| 洗衣机 | 8 | 35 | 280 |
| 桌子 | 7 | 75 | 525 |
| 打印机 | 35 | 52 | 1820 |
| 合计 | 3175 | ||
最终项目实施完毕后,结算是根据实际实施数量*投标单价进行结算,根据经验我们能判断最终那些数量会增加实施,那些数量会减少实施,假设实际实施数量如下(电脑增加了 3 台,空调减少了 2 台…)
| 采购内容 | 采购数量 | 投标单价 | 投标报价合计 |
| 电脑 | 13 | ||
| 空调 | 18 | ||
| 洗衣机 | 7 | ||
| 桌子 | 7 | ||
| 打印机 | 38 | ||
| 合计 | 3175 | ||
由此产生了需求,求出在总报价不变的情况下,针对最终实施数量会减少的部分,尽可能的报低单价,针对最终实施数量会增加的部分报高单价,对于各个商品的单价变化幅度有一个同一的范围,以达到结算的时候利益最大化。
最终需求:在已知最终数量的情况下,报价单价策略应该填多少,利益才能最大化,也就是我们需要求的那个最大值。

问题分析
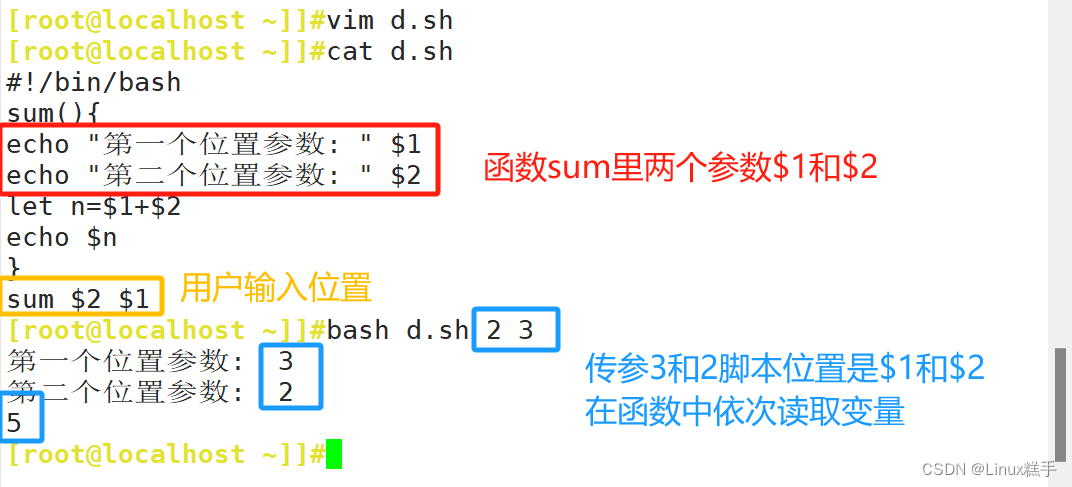
我们对上面图片中的内容进行划分,从左到右分别为A、B、C、D、E、F、G列,D列各行的值为B*C,在最后还有对于所有采购商品的总价汇总。A、B、C、E列的值已经给出,现在需要求出D、F、G列的内容,此处略过D列数据的求解,着重分析F列的求值。
假设X列从上至下的值为一个数组 $(x_1, x_2, …, x_n)
,那么
F
列的值为
,那么F列的值为
,那么F列的值为(f_1, f_2, …, f_n)$,B列的值为(b_1, b_2, …, b_n),C列的值为(c_1, c_2, …, c_n),按照题目中所给的条件,我们可以得到以下两个约束条件:
- 一个1 * n的矩阵B与一个n * 1的矩阵C点乘后的结果 == 一个1 * n的矩阵B与一个n * 1的矩阵F点乘的结果
- f i ∗ ( 1 − m a x D e c r e a s e ) < = f i < = f i ∗ ( 1 + m a x I n c r e a s e ) f_i * (1 - maxDecrease) <= f_i <= f_i * (1 + maxIncrease) fi∗(1−maxDecrease)<=fi<=fi∗(1+maxIncrease)
- s u m = ∑ i = 1 n f i sum = \sum_{i=1}^n f_i sum=i=1∑nfi
仔细一分析过后,我们可以发现我们仔细分析了一下,我们可以发现,这是一个线性规划问题,没错,就是高中时期常常出现在填空题里的那个属于送分题的线性规划问题,只不过从高中时期的不超过4个限制条件变成了n个而已,没有什么难的。此时我们开始思考一个问题,那就是如何构造一个多数线性规划模型,并能够针对限制条件数量未知的情况来进行模型的快速调用,并实现限制条件和结果的输入以及得出。
所幸,Python中有这么一个库,能够实现我们当前面临问题的完美解决。
相关依赖库
主要介绍实现过程中的几个重要库,其余库的具体安装要求请参照项目下的
requirements.txt文件,以下是关于几个重要库的介绍。
PuLP
如果你在百度里搜索Python PuLP,你会发现与之相关联的词条除了一个同名的乐队之外,还有优化问题以及混合整数规划(MILP)这两个词条。如果你在google里面搜索同样的词条,至少前一页都是Pulp库以及线性规划相关的内容。不同的搜索引擎都能找到的共同点就是,pulp在线性规划问题方面的使用。
在pulp库的文档中你可以看到有这么一个关于猫粮中原料配比的问题,如果你看不懂英文,可以看下面的这个文档,这是某个知乎上的前人写的说明,基本上已经将原本文档中的内容进行了翻译,大家可以着重看代码部分:
# 导入 PulP
from pulp import *
# 建立线性规划问题,指定名称:CatFood, 问题的目标:求解最小值 LpMinimize
prob = pulp.LpProblem(name='CatFood', sense=LpMinimize)
# 定义变量: 鸡肉占比,设置下限值为 0 , 不能是负数
x1 = LpVariable("鸡肉占比", lowBound=0)
# 定义变量: 牛肉占比,设置下限值为 0 , 不能是负数
x2= LpVariable("牛肉占比", lowBound=0)
# 将目标函数用 += 方式附加到 prob 变量
prob += 0.013*x1 + 0.008*x2, "最小成本"
# 将约束条件用 += 方式附加到 prob 变量,注意区别是约束条件有判断操作符
prob += x1 + x2 == 100, "占比总和"
prob += 0.100 * x1 + 0.200 * x2 >= 8.0, "蛋白质含量"
prob += 0.080 * x1 + 0.100 * x2 >= 6.0, "脂肪含量"
prob += 0.001 * x1 + 0.005 * x2 <= 2.0, "纤维含量"
prob += 0.002 * x1 + 0.005 * x2 <= 0.4, "盐含量"
# 将问题输出为 lp 文件
prob.writeLP('catfood.lp')
此处并没有将问题进行解决,只是通过代码的描述,将问题的内容实现了自生成,你会得到一个catfood.lp文件,里面的内容长这样:
# 查看输出的 lp 文件
! cat catfood.lp
\* CatFood *\
Minimize
最小成本: 0.008 牛肉占比 + 0.013 鸡肉占比
Subject To
占比总和: 牛肉占比 + 鸡肉占比 = 100
盐含量: 0.005 牛肉占比 + 0.002 鸡肉占比 <= 0.4
纤维含量: 0.005 牛肉占比 + 0.001 鸡肉占比 <= 2
脂肪含量: 0.1 牛肉占比 + 0.08 鸡肉占比 >= 6
蛋白质含量: 0.2 牛肉占比 + 0.1 鸡肉占比 >= 8
End
是的,他没什么用处,只是给我们看看的。but,这只是这个知乎的作者没有认真思考照单全抄的缘故,因为此时的我们完全可以将上面的问题通过当前库进行解决(一个库如果只能将问题进行描述但不能实现解决,这就相当于上厕所不仅没有纸而且没有水),只需再加几行代码:
# 用求解器解决问题
prob.solve()
# 查看求解器的状态
# 返回的状态是 : Not Solved, Infeasible, Unbounded, Undefined, Optimal
# Optimal 就是有最优解
print("Status:", LpStatus[prob.status])
# 查看变量的值
for v in prob.variables():
print(v.name, "=", v.varValue, '%')
print( "每100克猫粮的最小成本 = ", value(prob.objective))
添加以上代码后可以实现在控制台输出最终的结果。
此时,我们又面临一个问题,如何添加多个参数,可能很多很多个参数,是的,这个问题有点让人头秃,but,在这里,我不得不说,写了这个库的人真是个天才,因为他提供了一个addVariable()方法,使得我们可以通过遍历已有的数据实现对问题限制条件的批量化添加,比如这样:
for i in range(10):
v = pulp.LpVariable(key_list[i], lowBound=original_price[i], upBound=original_price[i] * (1 + max_increase),
cat='Continuous')
MyProblem.addVariable(v)
其中key_list中元素为str类型,original_price中元素为数字类型,max_increase是数字。
最终,我们通过构建这个规划问题,实现了投标单价修改值的求解。具体代码由于当前代码属于商用的开发阶段,不方便直接展示,具体实现请查看version包下的budget_bid_price_version_01.py文件,所有的代码已上传到github仓库。