代码随想录算法训练营第16天 | 104.二叉树的最大深度， 111.二叉树的最小深度，222.完全二叉树的节点个数

news2024/10/2 22:27:11

二叉树理论基础：

https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

104.二叉树的最大深度

题目链接：https://leetcode.cn/problems/maximum-depth-of-binary-tree/

思路:（递归法）

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

这一点其实是很多同学没有想清楚的，很多题解同样没有讲清楚。

我先用后序遍历（左右中）来计算树的高度。

确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。

class solution {
public:
    int getdepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftdepth = getdepth(node->left);       // 左
        int rightdepth = getdepth(node->right);     // 右
        int depth = 1 + max(leftdepth, rightdepth); // 中
        return depth;
    }
    int maxDepth(TreeNode* root) {
        return getdepth(root);
    }
};

226.翻转二叉树

题目连接：https://leetcode.cn/problems/invert-binary-tree/

思路：

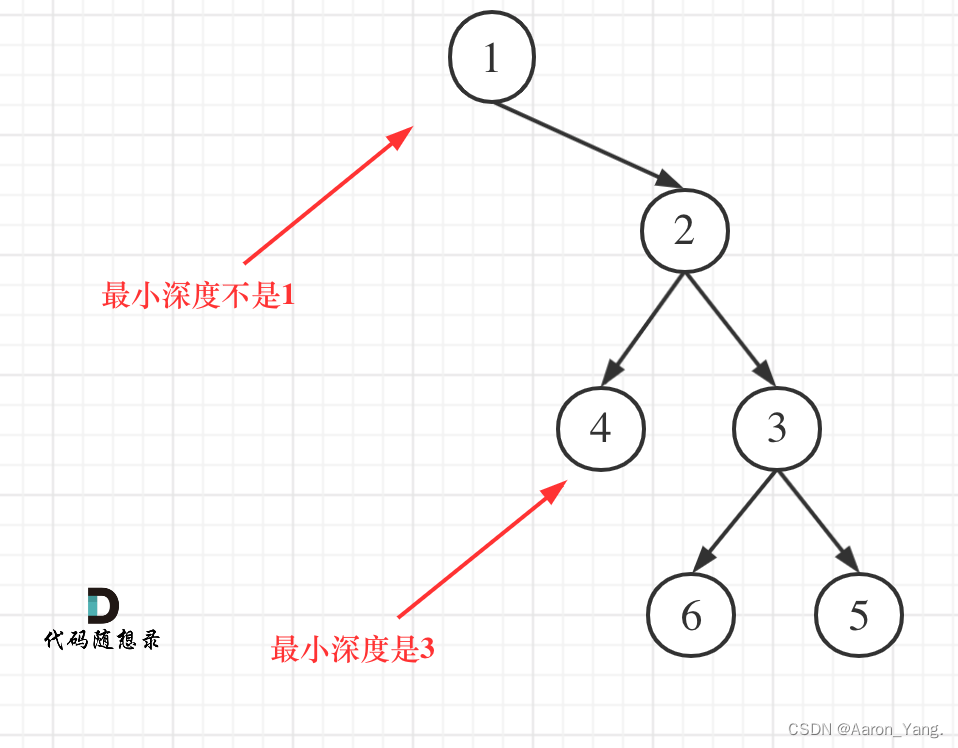
本题有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解。
题目中说的是：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。
什么是叶子节点，左右孩子都为空的节点才是叶子节点
在这里插入图片描述
int result = 1 + min(leftDepth, rightDepth);
这个代码就犯了此图中的误区：
如果这么求的话，没有左孩子的分支会算为最短深度。

所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

遍历的顺序为后序（左右中），可以看出：求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑

class Solution {
    public int minDepth(TreeNode root) {
        return getDepth(root);
    }

    public int getDepth(TreeNode node) {
        if(node == null)
            return 0;
        int leftDepth = getDepth(node.left);
        int rightDepth = getDepth(node.right);
        // 特殊判断
        // 如果左子树为空，右子树不为空
        if(node.left==null && node.right!=null)
            return 1 + rightDepth;
        // 如果左子树不为空，右子树为空
        if(node.left!=null && node.right==null)
            return 1 + leftDepth;
        
        return 1+Math.min(leftDepth,rightDepth);
    }
}

222.完全二叉树的节点个数

思路：

首先按照普通二叉树的逻辑来求。

这道题目的递归法和求二叉树的深度写法类似，先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一（加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

class Solution {
    public int countNodes(TreeNode root) {
        return getTreeNodes(root);
    }

    private int getTreeNodes(TreeNode node){
        if(node==null)
            return 0;
        return 1+getTreeNodes(node.left)+getTreeNodes(node.right);
    }
}