1. 线性回归

视频：https://www.bilibili.com/video/BV1PX4y1g7KC/?spm_id_from=333.999.0.0&vd_source=eb04c9a33e87ceba9c9a2e5f09752ef8
课件：https://zh-v2.d2l.ai/chapter_linear-networks/linear-regression.html
课上ppt：https://courses.d2l.ai/zh-v2/assets/pdfs/part-0_8.pdf

机器学习最基础应用。

1. 模型

1. 房价预测–一个简化的模型

2. 拓展到一般化线性模型

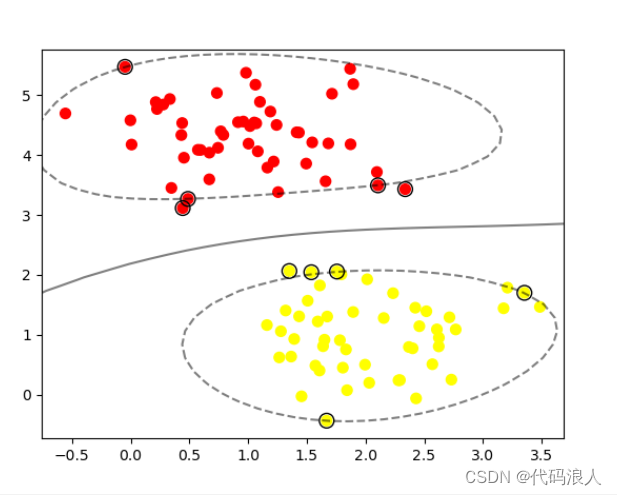
3. 线性模型可以看做是单层神经网络

每个箭头代表对应的weight，输入和weight看作是同一层。
神经网络起源于生物神经科学，早期部分模型来来源于神经学的背景，目前神经网络的发展已不再局限于神经学。

2. 预测

1. 衡量预估质量

2. 训练数据

3. 求解模型

4. 显示解

线性模型是有显示解的。

5. 总结

2. 基础优化算法

视频：https://www.bilibili.com/video/BV1PX4y1g7KC/?p=2&spm_id_from=pageDriver&vd_source=eb04c9a33e87ceba9c9a2e5f09752ef8
课件：https://zh-v2.d2l.ai/chapter_linear-networks/linear-regression.html
课上ppt：https://courses.d2l.ai/zh-v2/assets/pdfs/part-0_9.pdf

1. 梯度下降

选择学习率
计算梯度是模型训练最贵的部分。【耗资源】

2. 小批量随机梯度下降

每次计算梯度，要对整个损失函数求导，损失函数是所有样本的平均损失，每次求梯度要算所有样本，而且一般需要多几百次或上千次的下降计算，计算代价太大。

b很大计算近似很精确，极限计算所有样本，计算太大。
b很小计算近似不很精确，计算梯度容易，计算梯度的复杂度跟样本个数线性相关。

3. 总结

练习

3. 线性回归的从零开始实现

不使用框架提供的计算，使用简单tensor计算实现细节。
pip install d2l

%matplotlib inline
from matplotlib_inline import backend_inline
import random
import torch
from d2l import torch as d2l

# 绘图
def use_svg_display():
  """使用svg格式在Jupyter中显示绘图"""
  backend_inline.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):
  """设置matplotlib的图表大小"""
  use_svg_display()
  d2l.plt.rcParams['figure.figsize'] = figsize

# 构造人造数据集 知道真实的w b
def synthetic_data(w, b, num_expamples):
  """生成y=Xw+b+噪声"""
  X = torch.normal(0, 1, (num_expamples, len(w)))  # 用于生成服从正态分布的随机数(mean,std,size,device,requires_grad)
  print(X.shape)
  y = torch.matmul(X, w) + b # torch.matmul() 多维张量相乘，有广播机制
  y += torch.normal(0, 0.01, y.shape) # 加一些噪声
  return X, y.reshape((-1, 1)) # 把y重新定义为一个列向量返回， -1自动推断，每行只有一列元素

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print(features.shape, labels.shape)
print(features[0], labels[0])
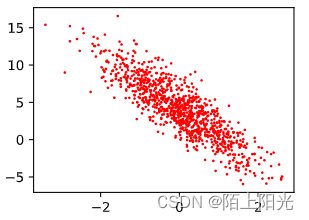
# 调用绘图
set_figsize()
# .detach() 部分torch版本需要写--从计算图中detach出来，否则无法调用numpy()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1, 'red') # scatter(x,y,点的大小,颜色) 绘制散点图

# 读取小批量
def data_iter(batch_size, features, labels):
  num_expamples = len(features)
  indices = list(range(num_expamples))
  random.shuffle(indices)
  for i in range(0, num_expamples, batch_size):
    batch_indices = torch.tensor(indices[i:min(i+batch_size, num_expamples)])
    # print(batch_indices)  # tensor([409, 128, 465,  85, 487, 117, 767, 311, 176, 119])
    yield features[batch_indices], labels[batch_indices]

# 初始化模型参数
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# 定义模型
def linreg(X, w, b):
  """线性回归模型"""
  return torch.matmul(X, w) + b

# 定义损失函数
def squared_loss(y_hat, y):
  """均方损失"""
  return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2  # 次数没有除以样本数 没有做平均

# 定义优化算法
def sgd(params, lr, batch_size):
  """
  小批量随机梯度下降
  params: weight b参数 参数list
  """
  with torch.no_grad(): # 更新的时候不需要参与计算梯度
    for param in params:
      param -= lr * param.grad / batch_size  # 上面求均方损失没有做除以样本数做均值，这里除以样本数做均值是一样的效果
      param.grad.zero_() # 调用一次梯度就清零一次 下一个使用梯度就不会跟上一次的梯度相关了

# 超参数的选择，会给模型带来什么样的效果
num_epochs = 3
# num_epochs = 10  
batch_size = 10
lr = 0.03
# lr = 0.001  # 学习率太小
# lr = 10  # 学习率太大
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
  for X, y in data_iter(batch_size, features, labels):
    # print(X)
    # print(y)
    # break
    # X和y的小批量损失
    l = loss(net(X, w, b), y) # 预测y_head 求损失--长为一个批量大小的向量
    # print(l.shape)  # torch.Size([10, 1])
    # 因为l的形状是（batchsize，1）而不是一个标量，需要将l中的所有元素被加到一起 并以此计算关于[w,b]的梯度
    # debug TypeError: unsupported operand type(s) for *: 'float' and 'NoneType'
    l.sum().backward()  # 调用梯度计算 求和后算梯度
    sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
  # 数据扫完一遍 一个epoch做完，评估下整个模型的效果 loss
  with torch.no_grad(): 
    train_l = loss(net(features, w, b), labels)
    print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
    
# 真实的w b 跟模型学到的 w b的区别
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
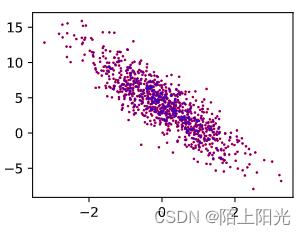
d2l.plt.scatter(features[:, 1].detach().numpy(), (torch.matmul(features, w) + b).detach().numpy(), 0.1, 'blue',
                 label='y=torch.matmul(X, w)+b-Epoch[{}]'.format(epoch))

torch.Size([1000, 2])
torch.Size([1000, 2]) torch.Size([1000, 1])
tensor([-0.5251, -1.0781]) tensor([6.8216])
epoch 1, loss 0.038617
epoch 2, loss 0.000136
epoch 3, loss 0.000047
w的估计误差: tensor([ 0.0004, -0.0009], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0002], grad_fn=<RsubBackward1>)
[<matplotlib.lines.Line2D at 0x7cc7b37cc580>]

4. 线性回归的简洁实现

代码模板：

1. 数据如何读取
2. 模型的定义
3. 参数的初始化
4. 损失函数
5. 训练模块

code

import numpy as np
import torch
from torch.utils import data # 提供数据处理工具
from d2l import torch as d2l

# 构造人造数据集 知道真实的w b
def synthetic_data(w, b, num_expamples):
  """生成y=Xw+b+噪声"""
  X = torch.normal(0, 1, (num_expamples, len(w)))  # 用于生成服从正态分布的随机数(mean,std,size,device,requires_grad)
  # print(X.shape)
  y = torch.matmul(X, w) + b # torch.matmul() 多维张量相乘，有广播机制
  y += torch.normal(0, 0.01, y.shape) # 加一些噪声
  return X, y.reshape((-1, 1)) # 把y重新定义为一个列向量返回， -1自动推断，每行只有一列元素

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

def load_array(data_arrays, batch_size, is_train=True): # 加载数据
  """构造一个pytorch数据迭代器"""
  dataset = data.TensorDataset(*data_arrays)
  return data.DataLoader(dataset, batch_size, shuffle=is_train) # shuffle 是否要对数据做随机打乱处理

batch_size = 10
data_iter = load_array((features, labels), batch_size) # dataset传的是一个元组，X y都上传，否则对应数据为0，数据迭代错误
# print(data_iter)  # 返回的是一个可迭代对象
# print(iter(data_iter))  # 返回的是一个迭代器 然后可以使用next()访问。
# next(iter(data_iter))
# print(enumerate(data_iter)) # 返回的是一个迭代器 然后可以使用next()访问 或者遍历
# next(enumerate(data_iter))  # 
next(iter(data_iter)) # iter python函数将可迭代对象转成迭代器

# nn是神经网络的缩写
from torch import nn

# 定义模型 nn.Linear第一个参数是输入的特征数，第二个参数是输出的特征数.
# Sequential 容器list 把要执行的层按执行顺序放在一起
net = nn.Sequential(nn.Linear(2, 1))

# 初始化模型参数
# net[0] 第零层 索引值是层list的位置 通过索引访问每一层
net[0].weight.data.normal_(0, 0.01) # .data 真实值
net[0].bias.data.fill_(0)  # 填充为0

# 定义损失函数
loss = nn.MSELoss() # 均方误差

# 定义优化器--优化算法  SGD(网络的参数， 指定学习率)
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

# 开始训练
num_epochs =3
for epoch in range(num_epochs):
  for X, y in data_iter:
    l = loss(net(X), y) # net()里面自带了w b参数，传参时不需要再传入 
    trainer.zero_grad() # 梯度先清零
    l.backward()   # 调用backward 计算梯度
    trainer.step()  # 调用step() 对模型做一次更新
  l = loss(net(features), labels)
  print(f'epoch: {epoch}, loss: {l:f}') # {l:f} 以浮点数的格式输出 否则可能是输出的科学计数法

w = net[0].weight.data
b = net[0].bias.data
print('w的估计误差： ', true_w - w)
print('b的估计误差： ', true_b - b)

epoch: 0, loss: 0.000204
epoch: 1, loss: 0.000100
epoch: 2, loss: 0.000100
w的估计误差：  tensor([[0.0002, 0.0002]])
b的估计误差：  tensor([0.0003])

小结

• 我们可以使用PyTorch的高级API更简洁地实现模型。
• 在PyTorch中，data模块提供了数据处理工具，nn模块定义了大量的神经网络层和常见损失函数。
• 我们可以通过_结尾的方法将参数替换，从而初始化参数。

QA

1. colab上也可以安装d2l库， pip install colab
2. 便宜的平台： colab  云【不用的时候一定要关机】
3. 为什么使用平方损失而不是绝对差值。
	有区别但不大，后续会讲，绝对差值在0处的导数有点难求。都可以用。
4. 损失为什么要求平均？
	平均后梯度会在数值上不会太大也不会太小，不除以n的话可以把学习率除以n。不管批量大小多大，计算的梯度总是差不多的，方便调学习率。
5. 线性回归损失函数一般都是MSE
6. 神经网络是通过误差反馈修改参数，凡是神经元没有反馈误差这一说，是人为推导的吗？
	误差反传，跟神经元有一点关系。hebb理论。感知机模型来自于神经学，本质上是一个梯度下降
7.  物理实验中经常使用n-1代替n求误差，这个的误差也能用n-1代替n吗
	都可以。最小化损失，跟损失值没关系。
8. gd梯度下降-sgd随机梯度下降怎么找到合适的学习率，有什么好的方法吗
	1）：找一个对lr不敏感的算法   
	 2）合理的参数初始化 --数值稳定性
	 3） 优化器有方法很快的找lr的一个区间
9. batchsize会影响最终模型结果吗，过小会导致最终累积的梯度计算不准确吗？ 
	过小好，过大不行。 batchsize越小对收敛越好，越小噪音越大，一定噪音对神经网络是个好事情，更鲁棒泛化性更好。 
10. 过拟合欠拟合的情况下，学习率和批次应该如何调整？
	学习率和批次理论上一般不会影响到最终收敛结果。
11. batchsize大小数据集做网络训练，网络中的每个参数更新时减去的梯度是batchsize中每个样本对应参数梯度求和后取均值。
	梯度是线性的，损失是每个样本相加，等价于每个样本求梯度再求均值
12. 随机梯度下降的“随机”指的是 批量大小一样，样本随机，随机采样批量个样本元素。
13. 深度学习中，设置损失函数需要考虑正则吗？
	需要考虑正则，但是在别的地方设置正则，一般不放在损失函数中。
14. 为什么机器学习优化算法都采用梯度下降（一阶求导算法），而不用牛顿法（二阶求导发），收敛速度更快，一般能算出一阶导，二阶导也应该能算。
	二阶导很难算，不一定能算，一阶导是向量，二阶导是矩阵，可以做近似二阶导，但真正牛顿法做不了。
	统计模型--损失函数，优化模型--用什么算法求解，两个都是错误模型，一般求不到最优解。收敛快不快不关心，关系的是收敛到哪个地方【最优】。收敛不一定快，泛化性也不一定比一阶导做的好。
	学术上有研究，生产上一般用一阶导。
15. 学习率怎么除N呢，设置学习率的时候。
16. detach()作用：从梯度的计算图里面拉出来，就不再算梯度了。要算numpy就不参与梯度计算。 features[:, 1].detach().numpy(), (torch.matmul(features, w) + b).detach().numpy()
	detach就是pytorch的用法，新版本可能已经去掉先要detach一下的这个用法了
17. data_iter写法，每次都把所有输入load进去，数据太多内存会爆掉。
	数据太大，不能先load进内存，几百M数据load进去也可以。实际生成数据在硬盘里，每次读几个batch的数据进内存。
18. 这里的indices为什么要转化成tensor，不能直接用列表。
19. 使用生成器生成数据有什么优势呢？相比return 
	生成器能保证shuf后的数据都是被拿到过一次的，不需要提前设置batch，二是Python的写法就这样。
20. 如果样本大小不是批量数的整倍数，会随机剔除多余的数据吗？
	1）拿到小批次样本
	2）扔掉小批次
	3）从别的批次随机取数据补全
21. 优化算法里除以batchsize，最后一个batch里样本个数小于batchsize也没有关系，数据足够多，多一点少一点影响不大。用pytorch的trianer会帮我们做除以样本数的个数。
22. 这里学习率不做衰减吗，好的学习率衰减方法有？
   理论上SGD变小的话，lr要不断的变小。adaptive 适应性强的机器学习？ 会根据梯度的大小调整学习率，不做衰减也可以。
23. 怎么进行收敛的判断呢？直接人为设置epoch的大小吗？
	1）两个目标函数loss等相对变化不大，可以停止
	2）用验证集，精度结果变化不大，可以停止
	3）直觉选。先训一个大的，看学习曲线选。
	4） 算力支持，多迭代几次也没关系
24. 本质上我们为什么要用SGD？是因为大部分的实际loss太复杂，推导不出导数为0的解码？只能逐个batch去逼近？
	除了线性回归有显示解，其他都没有。解np问题，基本都没有最优解。
25. w可以随机初始化，也可以是固定值【设置随机种子】。
26. 实际有时候网络会输出nan，nan是怎么出现的？为什么不是inf？数值稳定性不是会导致inf吗？
 求导有除法，会导致除0 除inf会导致这个问题。数值稳定性后面会讲。
27. 定义网络层后一定要手动设置参数初始值吗？ 
	不一定，有默认的初始值。
28. l.backward() 是调用的pytorch自定义的 back propogation[反向传播]
29. 外层训练最后一行l = loss(net(features), labels)就是为了print吗。这里梯度不需要清零，因为我们不需要backward做梯度更新了，所以不需要清零，就是最终结果了。
30. 每个batch计算为什么梯度要清零。 
    因为pytorch不自动帮忙清零，不清零梯度会在上一次的结果上做累加，一直都是增长的。
31. 学习率设置过大会造成梯度爆炸（数值为NAN），但从数学理解上，上一次根据偏导数乘以学习率调整参数，就算向相反的反向调整，下一次不是就可以纠正过来吗，为什么还会爆炸
	后续课程会讲。