报名明年4月蓝桥杯软件赛的同学们，如果你是大一零基础，目前懵懂中，不知该怎么办，可以看看本博客系列：备赛20周合集
20周的完整安排请点击：20周计划
每周发1个博客，共20周。
在QQ群上交流答疑：

  首先说抱歉，最近得了“乙流”感冒，头晕眼屎多鼻塞咽痛，无力翻新或重写一篇新的“并查集”。所以本篇博客节选了《程序设计竞赛专题挑战教程》中“6.1 并查集”的内容。以后有机会再翻新。

第17周:  并查集

  并查集通常被认为是一种“高级数据结构”，可能是因为用到了集合这种“高级”方法。不过，并查集的编码很简单，数据存储方式也仅用到了最简单的一维数组。如果跟真正的高级数据结构（线段树、平衡树、LCA、莫队等等）这些大哥相比，并查集就是是小婴儿。并查集是“并不高级的高级数据结构”。
  并查集，英文Disjoint Set，直译为“不相交集合”。把它意译为“并查集”非常好，因为它概况了三个意思：并、查、集。并查集是“不相交集合上的合并、查询”。
  并查集精巧、实用，在算法竞赛中很常见，原因有三点：简单且高效、应用很直观、容易和其他数据结构和算法结合。并查集的经典应用有：判断连通性、最小生成树Kruskal算法、最近公共祖先（Least Common Ancestors, LCA）等。
  通常用“帮派”的例子来说明并查集的应用背景。一个城市中有n个人，他们分成不同的帮派；给出一些人的关系，例如1号、2号是朋友，1号、3号也是朋友，那么他们都属于一个帮派；在分析完所有的朋友关系之后，问有多少帮派，每人属于哪个帮派。给出的n可能大于$10^6$。如果用并查集实现，不仅代码很简单，而且复杂度几乎是O(1)的，效率极高。
  并查集效率高，是因为用到了“路径压缩”这一技术。 不用路径压缩，并查集就是翅膀被拔了毛的鸟，飞不起来。“路径压缩”这么神奇，会不会很难？不用担心，它的代码仅有1行。

1. 并查集的基本操作

  并查集：将编号分别为1~n的n个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在集合。并查集适合处理不同集合的关系，它有三个基本操作：初始化、合并、查找。用本章开头的“帮派”为例子说明这三个基本操作。
  （1）初始化。定义一维数组int s[]，s[i]是结点i的并查集，开始的时候，还没有处理点与点之间的朋友关系，所以每个点属于独立的集，直接初始化s[i] = i，例如结点1的集s[1] = 1。
  下面是图解，左边给出了结点与集合的值，右边画出了它们的逻辑关系。为了便于讲解，左边区分了结点i和集s：把集的编号加上了下划线；右边用圆圈表示集，方块表示结点。
  初始时，每个结点的集是独立的，5个结点有5个集。

      图1 并查集的初始化
  是不是特别简单？仅仅只用到了一位数组这种最简单的数据结构。
  （2）合并，例如加入第一个朋友关系(1, 2)。在并查集s中，把结点1合并到结点2，也就是把结点1的集1改成结点2的集2，set[1] = set[2] = 2。此时5人的关系用4个集表示，其中set[2]包括2个结点。

      图2 合并(1,2)
  （3）继续合并，加入第二个朋友关系(1, 3)。
  首先查找结点1的集，是2，set[1] = 2，再继续查找2的集，是set[2] = 2，此时2的集是自己，查找结束。再查找结点3的集是set[3] = 3。由于set[2]不等于set[3]，下面把结点2的集2合并到结点3的集3。具体操作是修改set[2] = 3，此时，结点1、2、3都属于一个集：set[1] = 2、set[2] = 3、set[3] = 3。还有两个独立的集set[4] = 4、set[5] = 5。
  下面右图中，为简化图示，把结点2和集2画在了一起。

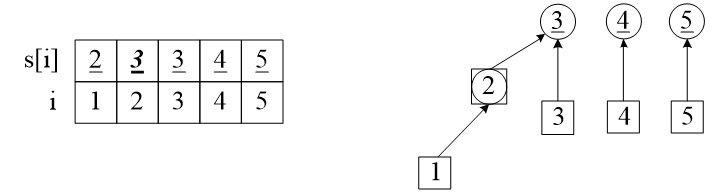
      图3 合并(1,3)

  （4）继续合并，加入第三个朋友关系(2, 4)。结果如下，请读者自己分析。合并的结果是：set[1] = 2、set[2] = 3、set[3] = 4、set[4] = 4。还有一个独立的集set[5] = 5。

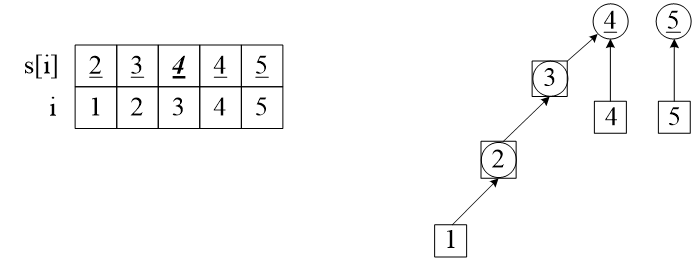
      图4 合并(2,4)

  （5）查找。查找某个结点属于哪个集。这是一个递归的过程，例如找结点1的集，递归步骤是：set[1] = 2、set[2] = 3、set[3] = 4、set[4] = 4，最后结点的值和它的集相等，就找到了根结点的集。
  （6）统计。统计有几个集。只要检查有多少结点的集等于自己，就有几个集。如果s[i] = i，这是一个根结点，是它所在的集的代表；统计根结点的数量，就是集的数量。上面的图示中，只有set[4] = 4、set[5] = 5，有2个集。
  从上面的图中可以看到，并查集是“树的森林”，一个集是一棵树，有多少棵树就有多少集。有些树的高度，可能很大，是O(n)的，变成了一个链表，出现了树的“退化”现象，使得递归查询十分耗时。后面将用“路径压缩”来解决这一问题。
  下面用例题给出3个基本操作的编码。

---

蓝桥幼儿园
【题目描述】蓝桥幼儿园的学生天真无邪，朋友的朋友就是自己的朋友。小明是蓝桥幼儿园的老师，这天他决定为学生们举办一个交友活动，活动规则如下：小明用红绳连接两名学生，被连中的两个学生将成为朋友。小明想让所有学生都互相成为朋友，但是蓝桥幼儿园的学生实在太多了，他无法用肉眼判断某两个学生是否为朋友。请你帮忙写程序判断某两个学生是否为朋友。
【输入描述】第1行包含两个正整数N,M，其中N表示蓝桥幼儿园的学生数量，学生的编号分别为1∼N。之后的第2∼M+1 行每行输入三个整数op,x,y。如果op = 1，表示小明用红绳连接了学生x 和学生yy。如果op=2，请你回答小明学生x和学生y是否为朋友。1≤N,M≤2×105，1≤x, y≤N。
【输出描述】对于每个op=2的输入，如果x和y是朋友，则输出一行YES，否则输出一行NO。

---

  下面是并查集的代码。
  （1）初始化init_set()。
  （2）查找find_set()。是递归函数，若x == s[x]，这是一个集的根结点，结束。若x != s[x]，继续递归查找根结点。
  （3）合并merge_set(x, y)。合并x和y的集，先递归找到x的集，再递归找到y的集，然后把x合并到y的集上。如下图所示，x递归到根b，y递归到根d，最后合并为set[b] = d。合并后，这棵树更长了，查询效率更低。

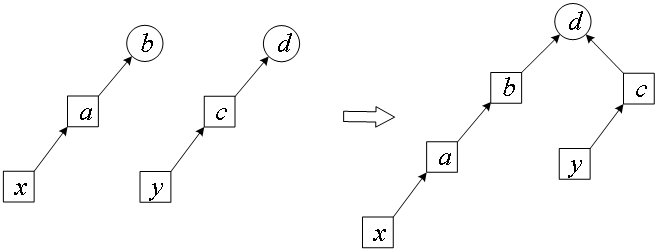
c++代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 8e5+5;
int s[N];
void init_set(){                  //初始化
   for(int i=1; i<=N; i++)  s[i] = i;
}
int find_set(int x){               //查找
  //if (x==s[x]) return x;
  //else return find_set(s[x]);   //这2行合并为下面的1行
    return x==s[x]? x:find_set(s[x]);
}
void merge_set(int x, int y){    //合并
    x = find_set(x);
    y = find_set(y);
    if(x != y) s[x] = s[y];      //y成为x的父亲，x的集是y
}
int main (){
    init_set();
    int n,m; cin>>n>>m;
    while(m--){
        int op,x,y; cin>>op>>x>>y;
        if(op == 1)   merge_set(x, y);
        if(op == 2){
            if(find_set(x)==find_set(y)) cout << "YES"<<endl;
            else                         cout << "NO"<<endl;
        }
    }
    return 0;
}

  代码超时！合并的时候，树变成了一个链表形状，出现了“退化”。下面用路径压缩来解决退化问题。

2. 路径压缩

  并查集之所以高效，根本原因是有这个优化技术：路径压缩。这个优化又简单又好！
  在上面的查询程序find_set()中，查询元素i所属的集，需要搜索路径找到根结点，返回的结果是根结点。这条搜索路径可能很长，导致超时。
  如何优化？如果在返回的时候，顺便把i所属的集改成根结点，那么下次再查的时候，就能在O(1)的时间内得到结果。由于find_set()是一个递归函数，在返回的时候，整个递归路径上的点，它们的集都改成了根结点。如下图所示，查询点1的集时，把路径上的2、3所属的集一起都改成了4，最后所有的结点的集都是4，下次再查询某个点所属的集，只需查一次。

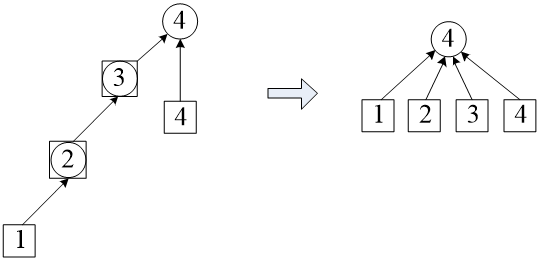
      图5 路径压缩
  路径压缩的代码非常简单。把上面超时代码中的find_set()改成以下路径压缩的代码。请读者思考为什么它的执行结果是上图所示。

int find_set(int x){
    if(x != s[x])   s[x] = find_set(s[x]);   //路径压缩
    return s[x];
}

  路径压缩对合并也有用，因为合并需要先查询，查询用到了路径压缩。
  路径压缩之前，查询和合并都是O(n)的。经过路径压缩之后，查询和合并平均都是O(1)的。并查集显示出了巨大的威力。
  下面用把“例题.蓝桥幼儿园”再写一遍。
C++代码

#include <bits/stdc++.h>
using namespace std;
const int N = 8e5+5;
int s[N];
void init_set(){                  //初始化
   for(int i=0; i<N; i++)  s[i] = i;
}
int find_set(int x){
    if(x != s[x])   s[x] = find_set(s[x]);   //路径压缩
    return s[x];
}
void merge_set(int x, int y){    //合并
    x = find_set(x);
    y = find_set(y);
    if(x != y) s[x] = s[y];      //y成为x的父亲，x的集是y
}
int main (){
    init_set();
    int n,m; cin>>n>>m;
    while(m--){
        int op,x,y; cin>>op>>x>>y;
        if(op == 1)   merge_set(x, y);
        if(op == 2){
            if(find_set(x)==find_set(y)) cout << "YES"<<endl;
            else                         cout << "NO"<<endl;
        }
    }
    return 0;
}

java代码

import java.util.Scanner;
public class Main {
    static int[] s;
    public static void initSet() {
        for (int i = 0; i < s.length; i++)  s[i] = i;        
    }
    public static int findSet(int x) {
        if (x != s[x])   s[x] = findSet(s[x]);        
        return s[x];
    }
    public static void mergeSet(int x, int y) {
        x = findSet(x);
        y = findSet(y);
        if (x != y)  s[x] = s[y];        
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = 8 * 100000 + 5;
        s = new int[N];
        initSet();
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        while (m-- > 0) {
            int op = scanner.nextInt();
            int x = scanner.nextInt();
            int y = scanner.nextInt();
            if (op == 1)       mergeSet(x, y);
            else if (op == 2) {
                if (findSet(x) == findSet(y))     System.out.println("YES");
                else                              System.out.println("NO");                
            }
        }
    }
}

python代码

N = 800_005
s = []                          #并查集
def init_set():                 #初始化    
for i in range(N): s.append(i)   
#s = list(range(N))             #2~4行可以改为这一行，定义和初始化并查集s。后面第14行的init_set()删除。
def find_set(x):                #有路径压缩优化的查询
    if(x != s[x]):  s[x] = find_set(s[x])   
    return s[x]
def merge_set(x, y):            #合并
    x = find_set(x)
    y = find_set(y)
    if(x != y):  s[x] = s[y]
n,m = map(int,input().split())    
init_set()
for i in range(m):
    op,x,y = map(int,input().split()) 
    if op==1:   merge_set(x, y);
    if op==2:
        if(find_set(x) == find_set(y)): print("YES")
        else:                           print("NO")

  一个字，”用并查，必压缩！“

3. 例题

3.1 合根植物

---

合根植物
【题目描述】w星球的一个种植园，被分成m×n个小格子（东西方向m行，南北方向n列）。每个格子里种了一株合根植物。这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？
【输入格式】第一行，两个整数m，n，用空格分开，表示格子的行数、列数（1<m,n<1000）。接下来一行，一个整数k，表示下面还有k行数据(0<k<100000)。接下来k行，第行两个整数a，b，表示编号为a的小格子和编号为b的小格子合根了。格子的编号一行一行，从上到下，从左到右编号。
【输出格式】输出一个整数表示答案。

---

  本题是并查集的简单应用，用并查集对所有植物做合并操作，最后统计有多少集。
  这是2017年第八届决赛真题。当年的题目还是挺简单的，现在恐怕不会这么出题了。想起来让人惆怅，时间往前跑，永远回不去。
c++代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int s[N];
int find_set(int x){
    if(x!=s[x])  s[x]=find_set(s[x]);
    return s[x];
}
int main(){
    int n,m,k;   scanf("%d%d%d",&n,&m,&k);
    for(int i=0;i<N;i++)  s[i]=i;   //初始化并查集
    while(k--){
        int a,b;   scanf("%d%d",&a,&b);
        int pa = find_set(a),pb=find_set(b);
        if(pa!=pb)  s[pa] = pb;    //合并并查集
    }
    int ans=0;
    for(int i=1;i<=n*m;i++)
        if(s[i]==i)  ans++;
    printf("%d",ans);
    return 0;
}

java代码

import java.util.Scanner;
public class Main {
    static int[] s;
    public static int findSet(int x) {
        if (x != s[x]) s[x] = findSet(s[x]);        
        return s[x];
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = 1000000 + 10;
        s = new int[N];
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int k = scanner.nextInt();
        for (int i = 0; i < N; i++)  s[i] = i;        
        while (k-- > 0) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();
            int pa = findSet(a);
            int pb = findSet(b);
            if (pa != pb) s[pa] = pb;            
        }
        int ans = 0;
        for (int i = 1; i <= n * m; i++) {
            if (s[i] == i)   ans++;            
        }
        System.out.println(ans);
    }
}

python代码
  下面的代码和上面的C++代码的逻辑稍有不同。初始化时，假设所有植物都不合根，答案ans = m×n。然后用并查集处理合根，合根一次，ans减一。

def find_set(x):                    #有路径压缩优化的查询
    if(x != s[x]):  s[x] = find_set(s[x])   
    return s[x]
def merge_set(x, y):
    x = find_set(x); y = find_set(y)
    if x == y:   return False       #原来就是同根的，不用合根
    s[y] = x
    return True                     #合根一次
m, n = map(int, input().split())
k = int(input())
s = list(range(m*n))                #并查集，定义、初始化 s=[0,1,2,3,……]
ans = m * n
for i in range(k):
    x, y = map(int, input().split())
    if merge_set(x, y):   ans -= 1   #合根一次，ans减一
print(ans)

3.2 修改数组

---

修改数组
【题目描述】给定一个长度为N的数组A = [A1, A2,…,AN]，数组中有可能有重复出现的整数。现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改A2, A3, …, AN。当修改Ai时，小明会检查Ai是否在A1~ Ai-1中出现过。如果出现过，则小明会给Ai加上1；如果新的Ai仍在之前出现过，小明会持续给Ai加1，直到Ai没有在A1~Ai-1中出现过。当AN也经过上述修改之后，显然A数组中就没有重复的整数了。现在给定初始的A数组，请你计算出最终的A数组。
【输入】第一行包含一个整数N(1≤N≤100000)，第二行包含N个整数A1, A2, …, AN (1≤Ai≤1000000)。
【输出】输出N个整数，依次是最终的A1, A2, …, AN

---

  这是一道好题，很难想到可以用并查集来做。
方法一：暴力
  先尝试暴力的方法：每读入一个新的数，就检查前面是否出现过，每一次需要检查前面所有的数。共有n个数，每个数检查O(n)次，所以总复杂度是$O(n^2)$的，超时。
方法二：hash
  容易想到一个改进的方法：用hash。定义vis[]数组，vis[i]表示数字i是否已经出现过。这样就不用检查前面所有的数了，基本上可以在O(1)的时间内定位到。
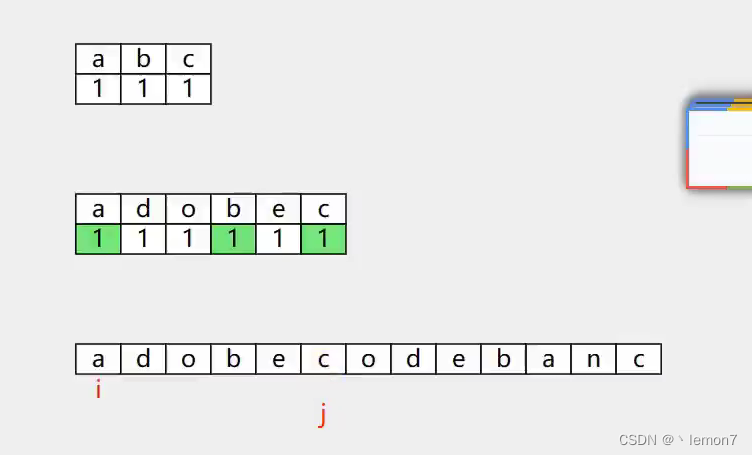
  然而，本题有个特殊的要求：“如果新的Ai仍在之前出现过，小明会持续给Ai加1，直到Ai没有在A1 ~Ai−1中出现过。”这导致在某些情况下，仍然需要大量的检查。以5个6为例：A[] = {6, 6, 6, 6, 6}。
   第一次读A[1]=6，设置vis[6]=1。
   第二次读A[2]=6，先查到vis[6]=1，则把A[2]加1，变为a[2]=7；再查vis[7]=0，设置vis[7]=1。检查了2次。
   第三次读A[3]=6，先查到vis[6]=1，则把A[3]加1得A[3]=7；再查到vis[7]=1，再把A[3]加1得A[3]=8，设置vis[8]=1；最后查vis[8]=0，设置vis[8]=1。检查了3次。
   …
   每次读一个数，仍需检查O(n)次，总复杂度仍然是$O(n^2)$的。
   下面给出hash代码，提交返回超时。
c++代码

#include<bits/stdc++.h>
using namespace std;
#define N 1000002   //A的hash，1≤Ai≤1000000
int vis[N]={0};     //hash:  vis[i]=1表示数字i已经存在
int main(){
    int n;	scanf("%d",&n);
    for(int i=0;i<n;i++){
	   int a; scanf("%d",&a);  //读一个数字
	   while(vis[a]==1) a++;   //若a已经出现过，加1。若加1后再出现，则继续加			
	   vis[a]=1;               //标记该数字
	   printf("%d ",a);        //打印
    }
}

方法三：并查集

  这题用并查集非常巧妙。
  上文提到，本题用Hash方法，在特殊情况下仍然需要大量的检查。问题出在“持续给Ai加1，直到Ai没有在A1 ~ Ai−1中出现过”。也就是说，问题出在那些相同的数字上。当处理一个新的A[i]时，需要检查所有与它相同的数字。
  如果把这些相同的数字看成一个集合，就能用并查集处理。
  用并查集s[i]表示访问到i这个数时应该将它换成的数字。以A[] = {6, 6, 6, 6, 6}为例。初始化时set[i] = i。

      图6 用并查集处理数组A
  图(1)读第一个数A[0] = 6。6的集set[6] = 6。紧接着更新set[6] = set[7] = 7，作用是后面再读到某个A[k] = 6时，可以直接赋值A[k] = set[6] = 7。
  图(2)读第二个数A[1] = 6。6的集set[6] = 7，更新A[1] = 7。紧接着更新set[7] = set[8] = 8。如果后面再读到A[k] = 6或7时，可以直接赋值A[k] = set[6] = 8或者A[k] = set[7] = 8。
  图三读第三个数A[2] = 6。请自己分析。
（1）C++代码。只用到并查集的查询，没用到合并。必须是“路径压缩”优化的，才能加快查询速度。没有路径压缩的并查集，仍然超时。
c++代码

#include<bits/stdc++.h>
using namespace std;
const int N=1000002;            
int A[N];
int s[N];                       //并查集
int find_set(int x){            //用“路径压缩”优化的查询
    if(x != s[x])  s[x] = find_set(s[x]);    //路径压缩
    return s[x];
}
int main(){
    for(int i=1;i<N;i++)  s[i]=i;      //并查集初始化
    int n;   scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&A[i]);
        int root = find_set(A[i]);    //查询到并查集的根
        A[i] = root;
        s[root] = find_set(root+1);   //加1
    }
    for(int i=1;i<=n;i++)  printf("%d ",A[i]);
    return 0;
}

java代码

import java.util.Scanner;
public class Main {
    static int[] A;
    static int[] s;
    public static int findSet(int x) {
        if (x != s[x])    s[x] = findSet(s[x]);        
        return s[x];
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = 1000002;
        A = new int[N];
        s = new int[N];
        for (int i = 1; i < N; i++)  s[i] = i;        
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            A[i] = sc.nextInt();
            int root = findSet(A[i]);
            A[i] = root;
            s[root] = findSet(root + 1);
        }
        for (int i = 1; i <= n; i++)   System.out.print(A[i] + " ");        
    }
}

python代码

def find_set(x):       #有路径压缩优化的查询
    if(x != s[x]):   s[x] = find_set(s[x])     #集的根是最新的一个数
    return s[x]
N=1000002 
s = list(range(N))     #并查集，定义、初始化 s=[0,1,2,3,……]
n = int(input())
A = [int(i) for i in input().split()]
for i in range(n):
    root = find_set(A[i])
    A[i] = root
    s[root] = find_set(root+1)     #加1
for i in A:  print(i,end = ' ')

4. 练习

并查集题目 https://www.luogu.com.cn/problem/list?tag=47&orderBy=difficulty&order=asc&page=1

贴完了博客，感冒症状似乎好了点。