链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
题目描述
陶陶刚上一年级,今天数学课上老师教了乘法和除法,老师留了一道课后习题,陶陶很快地写完了,现在想请你帮助他检查一下是否和答案一致。
初始值为 111,给定两个操作序列,判断操作结果是否相同。
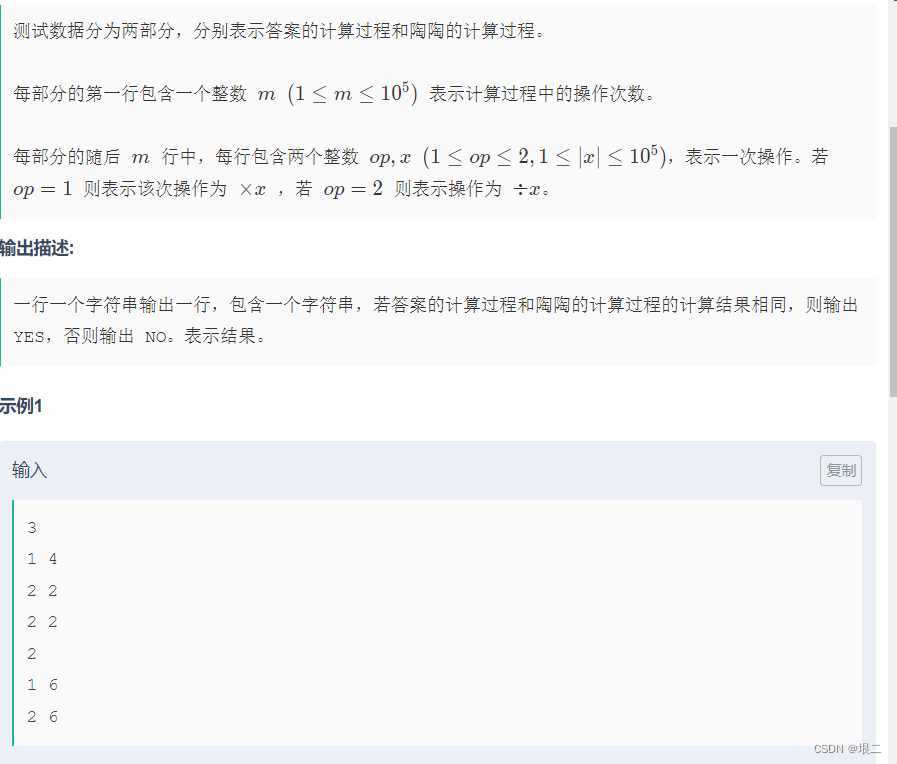

这道题如果直接模拟的话肯定是不能过全部示例的,会爆int。
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
vector<int> factorize(int n) {
vector<int> factors;
for (int i = 2; i * i <= n; ++i) {
while (n % i == 0) {
factors.push_back(i);
n /= i;
}
}
if (n > 1) {
factors.push_back(n);
}
return factors;
}
void solve() {
int q, cnt1 = 0, cnt2 = 0;
cin >> q;
vector<int> mp1(200005), mp2(200005);
while (q--) {
int op, x;
cin >> op >> x;
cnt1 += (x < 0 ? 1 : 0);
vector<int> a = factorize(abs(x));
if (op == 1) {
for (auto ai : a) {
mp1[ai]++;
}
} else {
for (auto ai : a) {
mp1[ai]--;
}
}
}
cin >> q;
while (q--) {
int op, x;
cin >> op >> x;
cnt2 += (x < 0 ? 1 : 0);
vector<int> a = factorize(abs(x));
if (op == 1) {
for (auto ai : a) {
mp2[ai]++;
}
} else {
for (auto ai : a) {
mp2[ai]--;
}
}
}
cout << (mp1 == mp2 && cnt1 % 2 == cnt2 % 2 ? "YES" : "NO");
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int _ = 1;
//cin >> _;
while (_--) {
solve();
}
return 0;
}这段代码使用了质因数分解和统计质因数出现次数的方法来判断两个操作序列是否相同。
在 factorize 函数中,通过遍历从 2 开始到根号 n 的所有数,将能整除 n 的数作为质因数,并将其存储在一个向量中。如果 n 仍然大于 1,表示 n 自身就是一个质因数,将其加入向量。最后返回质因数向量。
在主函数 solve 中,通过对每个操作进行因式分解,将质因数的出现次数记录在 mp1 和 mp2 中。然后通过比较两个 mp 向量是否相等,以及比较 cnt1 和 cnt2 的奇偶性是否相同来判断两个操作序列是否相同。
这种方法的核心思想是利用质因数分解将一个数拆分成质因数的乘积,然后通过比较质因数的出现次数来判断两个数是否相同。请注意,这种方法只能判断两个操作序列是否相同,而不能得到具体的操作步骤。
补充:
分解质因数模板:
#include <iostream>
using namespace std;
int main ()
{
int n,i=2;
cin>>n;
cout<<n<<"=";
do {
while(n%i==0) {
cout<<i;
n=n/i;
if(n!=1) cout<<"*";
}
i++;
}
while(n!=1);
return 0;
}
素数判定:
1.
循环,将n除以2---n-1的整数,如果有其中一个数运算后的余数==0,n不为素数。
#include<iostream>
using namespace std;
int main()
{
int n;
cin>>n;
bool flag=1;
for(int i=2;i<n;i++){
if(n%i==0){
flag=0;
break;
}
}
if(flag)cout<<"YES";
else cout<<"NO";
return 0;
}2.素数的因子只有1和它本身。 如果数c不是素数,则还有其他因子。设a,b.定有一个大于sqrt(c) ,一个小于sqrt(c) 。所以m一定有一个小于等于其平方根的因数,那么验证素数时就只需要验证到其平方根就可以了。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
bool flag=1;
for(int i=2;i<sqrt(n);i++){
if(n%i==0){
flag=0;
break;
}
}
if(flag)cout<<"YES";
else cout<<"NO";
return 0;
}3.埃氏筛法
要得到自然数n以内的全部素数,必须把不大于根号n的所有素数的倍数剔除,剩下的就是素数。
#include<bits/stdc++.h>
using namespace std;
bool flag[104];
int main()
{
memset(flag,1,sizeof(flag));
flag[1]=0;
for(int i=2;i<=sqrt(100);i++){
if(flag[i]){
for(int j=2;j*i<=100;j++)flag[i*j]=0;
}
}
for(int i=1;i<=100;i++){
if(flag[i])cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}4.欧拉筛法:
找到一个素数后,就将它的倍数标记为合数,也就是把它的倍数筛掉;如果一个数没有被比它小的素数筛掉,那它就是素数。
欧拉筛法复杂度为线性。
例题:
素数个数
素数个数 - 洛谷
题目描述
求 1,2,⋯,N 中素数的个数。
输入格式
一行一个整数 N。
输出格式
一行一个整数,表示素数的个数。
题解:
数据范围是10的8次方,不能一个一个判断,要用欧拉筛法。
#include<bits/stdc++.h>
using namespace std;
int n,ans,prime[5800001];
bool visit[100000001];
int main()
{
cin>>n;
if(n<2){
cout<<0;
return 0;
}
for(register int i=2; i<=n;i++) {
if(!visit[i])prime[++ans]=i;
for(register int j=1; prime[j]*i<=n&&j<=ans; ++j) {
visit[i*prime[j]]=true;
if(!(i%prime[j])) break;
}
}
//for(int i=1; i<=ans; ++i) printf("%d\n",prime[i]);
cout<<ans;
return 0;
}