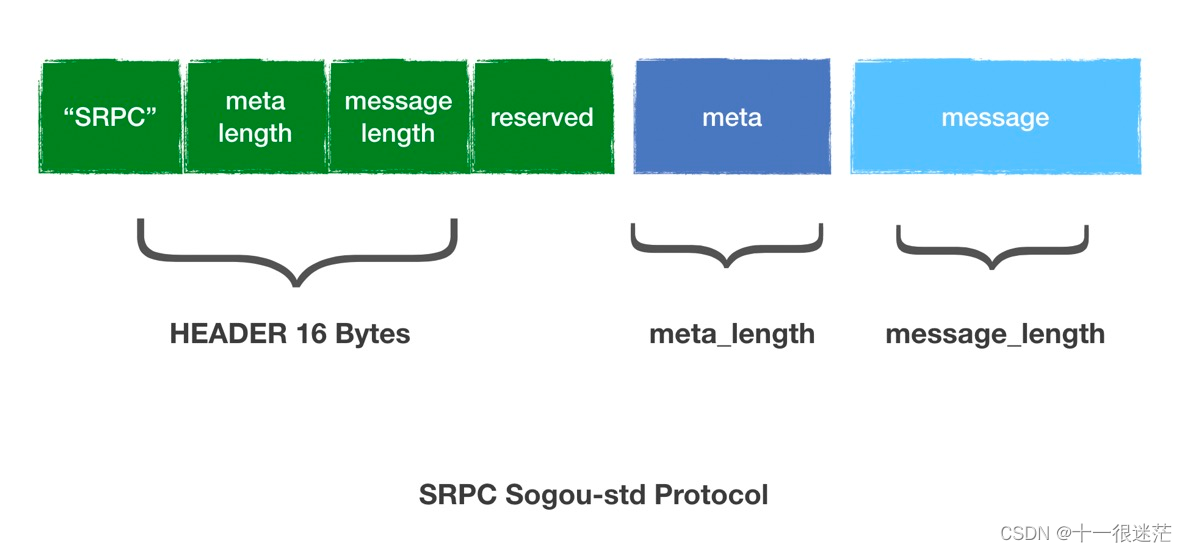
目录
🌈前言🌈:
📁 01背包问题
分析:
dp数组求解:
优化:滚动数组:
📁 完全背包问题
📁 总结
🌈前言🌈:
这篇文章主要是准备蓝桥杯竞赛同学所写,为你更好准备蓝桥杯比赛涉及的算法知识点。不知道你是否苦恼于不知算法从何学起,苦恼于网上资料稀少,或者复杂难懂,这篇文章就是帮助这部分同学的。
本篇文章适合基础较弱或零基础的同学,不会涉及晦涩难懂的公式,只是提供算法的思路,题解会从基础讲解,不会涉及大量复杂的证明,重要的是学废思想。
背包问题分为很多种,因为是基础学习,所以只是讲解最为简单的两种背包问题,其他的背包问题基本都是变形,例如多重背包问题。
01背包问题是有N种物品,每种物品就1件,让我们求在不超过背包容量M的前提下,拿到的物品总价值是多少。
完全背包问题是有N种物品,每种物品无限件,求在不超过背包容量M的前提下,最大物品价值是多少。
📁 01背包问题
2. 01背包问题 - AcWing题库

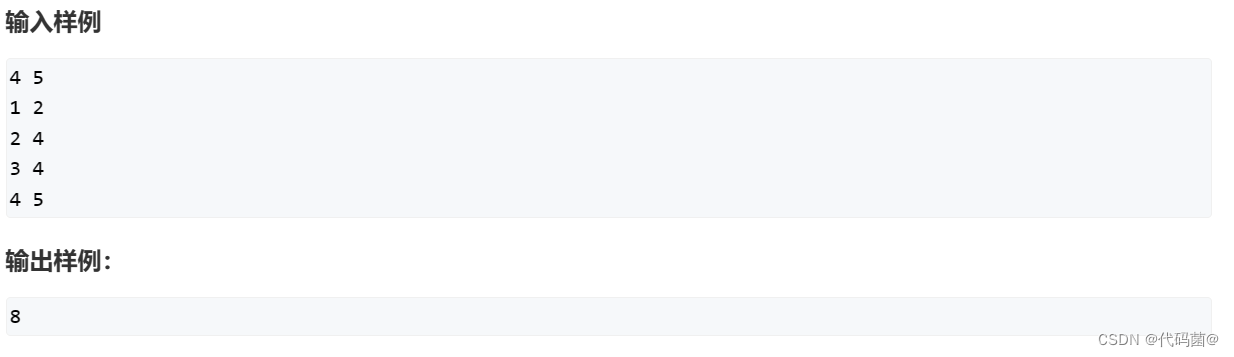
分析:
首先,我们拿到一道题目,首先要读懂题目。题目说,有N种物品,每种物品是1件。我们首先想到的肯定是暴力解法,通过不断的枚举来求出最大价值,例如第一件物品选不选,第二件物品选不选的思路来做。
这么想是没有问题的,这就是回溯算法,但是有个弊端是时间复杂度很高,达到2^N,所以我们就得换个思路了。
dp数组求解:
这里介绍一个B站up主大雪莱的一种方法,可以解决很多dp问题,即闫氏dp分析法。
i 表示前 i 件物品 ; j 表示 当前体积 ;dp[ i ][ j ] 任取前 i 个物品在总体积不超过 j 的所有选法的最大值。( 重点理解!!!)
我们通过枚举 j 从 0 到 M 求出,在当前 j 体积的情况下,选取前 i 件物品价值的最大值。
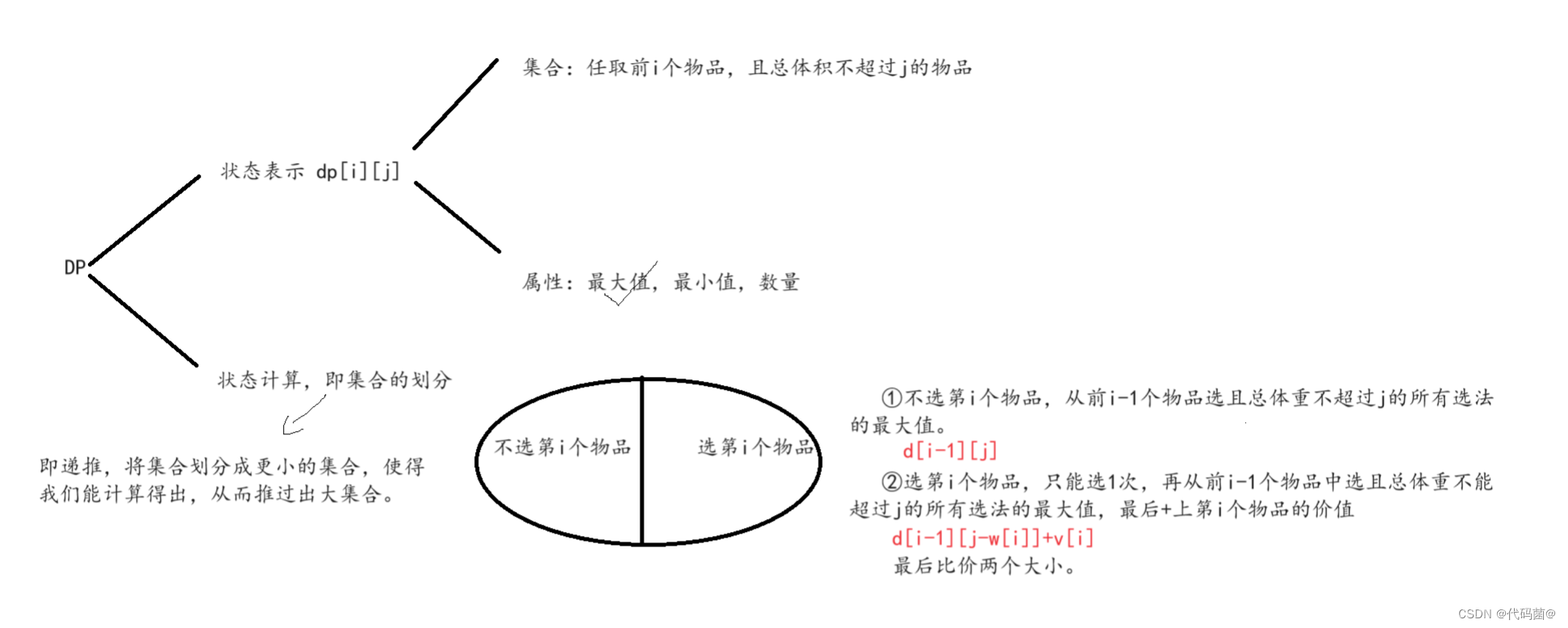
所以背包问题就是递推的问题,由小到大求出最大价值。而题目就是让我们求前n个物品总体重不超过m的情况,所以我们最后输出dp[n][m]即可。
举个例子,如下图所示。当前 i = 1 时,从第一件物品选择,总体积不超过 0,1,2 的情况下的最大值。
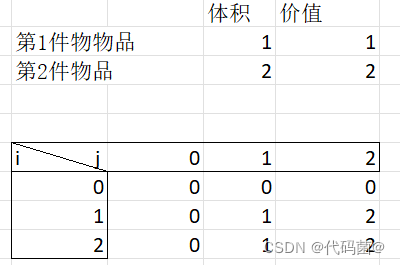
如果,你理清了上面这两幅图片,你也就搞懂了01背包问题了。下面,我们来看一下代码。
#include<iostream>
#include <algorithm>
using namespace std;
const int N =1010;
int n,m; n表示物品数量,m表示背包容量
int w[N],v[N]; w表示体重,v表示价值
int dp[N][N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>w[i]>>v[i];
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
{
if(j >= w[i])
dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
else
dp[i][j] = dp[i-1][j];
}
cout<<dp[n][m]<<endl;
return 0;
}优化:滚动数组:
以上就是通过二维数组来实现01背包问题,在做题过程中,我们发现第 i 层的最大值,是通过第 i - 1层推导出来的。
这里,我们就可以进行优化,将二维数组变为一维数组。因为 i 的作用就是标明前i个物品,而我们只是用了 i-1层 和 i层,这两层,因此就可以将上一层拷贝到下一层。
如下图所示,我们可以定义一个一维数组,从后往前枚举。因为是一维数组,并且我们要进行递推,所以前面会影响后面,如果我们从往后枚举,就不是上一层的最大值了(重点理解!!)
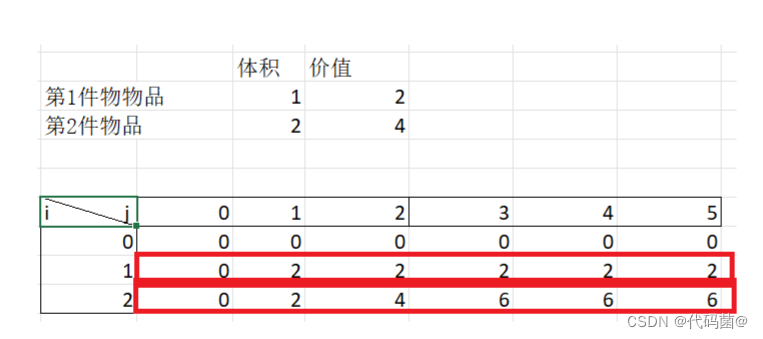
#include<iostream>
#include <algorithm>
using namespace std;
const int N =1010;
int n,m;
int w[N],v[N];
int dp[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>w[i]>>v[i];
for(int i=1;i<=n;i++)
for(int j=m;j>=w[i];j--)
{
dp[j] = max(dp[j],dp[j-w[i]] + v[i]);
}
cout<<dp[m]<<endl;
return 0;
}01背包问题,如果是初次接触,可能稍微有点繁琐,绕。所以需要自己多多画图,不断调试代码,画出每一层的每个选法的最大值方便更好的理解。
📁 完全背包问题
3. 完全背包问题 - AcWing题库

本文寻寻渐进的,如果你还没有搞懂01背包问题可能还需要多花时间理解,对于完全背包问题,也只是对01背包优化后一维数组的变形。
01背包的一维数组优化是从后往前遍历的,而完全背包问题则是从前往后遍历的。就这一点不同。
如果从前往后遍历,就意味着第i个物品可以选多个,所以就可以比较上一层的dp[ j ] 和 再选依次第i个物品的总价值。因为完全背包问题每种物品可以选择多次。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N];
int dp[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>w[i]>>v[i];
for(int i=1;i<=n;i++)
for(int j=w[i];j<=m;j++)
dp[j] =max(dp[j],dp[j-w[i]]+v[i]);
cout<<dp[m]<<endl;
return 0;
}📁 总结
以上,就是dp问题中基础的背包问题,以01背包为例子,如何分析dp背包问题,以及讲解01背包问题的优化,从而讲解了完全背包问题。
如果感觉对你有帮助,欢迎点赞,收藏,关注。Thanks♪(・ω・)ノ