为什么要进行特征降维?
特征对训练模型是非常重要的,用于训练的数据集包含一些不重要的特征,可能导致模型泛化性能
不佳
某些特征的取值较为接近,其包含的信息较少
希望特征独立存在对预测产生影响,两个特征同增同减非常相关,不会给模型带来更多信息
特征降维目的:
指在某些限定条件下,降低特征个数
特征降维涉及的知识面比较多,当前阶段常用的方法:
低方差过滤法、PCA(主成分分析)降维法、相关系数(皮尔逊相关系数、斯皮尔曼相关系数)
低方差过滤法
低方差过滤法:指的是删除方差低于某些阈值的一些特征
特征方差小:特征值的波动范围小,包含的信息少,模型很难学习到信息
特征方差大:特征值的波动范围大,包含的信息相对丰富,便于模型进行学习
低方差过滤API:
sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
实例化对象用于删除所有低方差特征
variance_obj.fit_transform(X)
X:numpy array格式的数据[n_samples,n_features]
返回值:训练集差异低于threshold的特征将被删除。
默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征
代码示例
import pandas as pd
# 读数据
data = pd.read_csv('垃圾邮件分类数据.csv')
print(data.shape)
#%%
# 过滤低方差法
from sklearn.feature_selection import VarianceThreshold
transformer = VarianceThreshold(threshold = 0.1)
transformer.fit_transform(data)
print(data.shape)
相关系数
为什么会使用相关系数?
相关系数:反映特征列之间(变量之间)密切相关程度的统计指标
常见2个相关系数:皮尔逊相关系数、斯皮尔曼相关系数
相关系数的值介于–1与+1之间,即–1≤ r ≤+1。其性质如下:
当 r>0 时,表示两变量正相关,r<0 时,两变量为负相关
当 |r|=1 时,表示两变量为完全相关,当r=0时,表示两变量间无相关关系
当 0<|r|<1时,表示两变量存在一定程度的相关。
且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
一般可按三级划分:|r|<0.4为低度相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关
皮尔逊相关系数
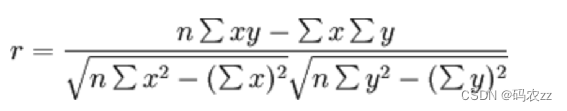
斯皮尔曼相关系数
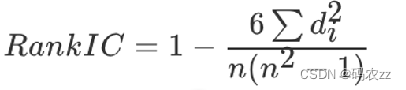
代码示例
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
iris_df = pd.DataFrame(iris.data,columns=iris.feature_names)
iris_df.corr() # 默认 皮尔逊相关系数
iris_df.corr('spearman') # 斯皮尔曼相关系数主成分分析PCA
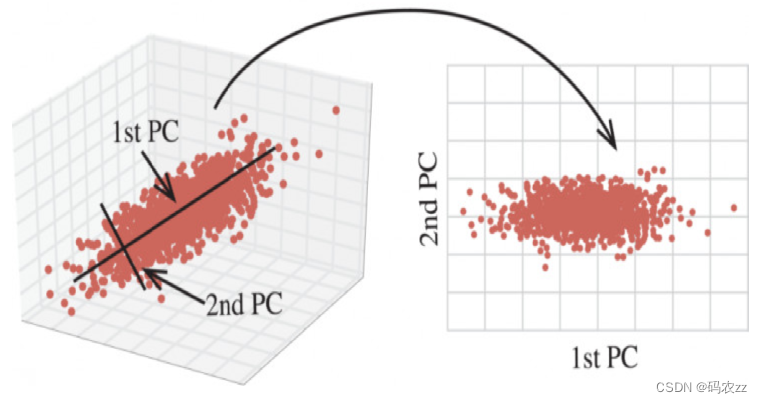
PCA 通过对数据维数进行压缩,尽可能降低原数据的维数(复杂度)损失少量信息,在此过程中会舍
弃原有数据、创造新的变量
主成分分析API:
sklearn.decomposition.PCA(n_components=None)
将数据分解为较低维数空间, n_components: 小数表示保留百分之多少的信息;
整数表示减少到多少特征 ,由20个特征减少到10个
mypcaobj.fit_transform(X)
返回值:转换后指定维度的array
代码示例
import pandas as pd
from sklearn.decomposition import PCA # decomposition 分解
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 加载数据
x,y = load_iris(return_X_y = True) # 只返回特征值和目标值
x
#%%
# 指定保留比例的信息
transformer = PCA(n_components=0.95)
# 标准化数据
x_scaled = StandardScaler().fit_transform(x)
# # pca
x_pca = transformer.fit_transform(x_scaled)
x_pca
#%%
# 画图确定x,y
import pandas as pd
x_pca_df = pd.DataFrame(x_pca, columns=['component_1', 'component_2'])
x_pca_df['label'] = y
#%%
import seaborn as sns
sns.scatterplot(data=x_pca_df,x='component_1',y='component_2',hue='label')