文章目录
- 51. 缺失的第一个正数
- 题目描述
- 代码与解题思路
- 52. 训练计划 II
- 题目描述
- 代码与解题思路
- 53. 子集
- 题目描述
- 代码与解题思路
- 54. 最小覆盖子串
- 题目描述
- 代码与解题思路
- 55. 从前序与中序遍历序列构造二叉树
- 题目描述
- 代码与解题思路
- 56. 零钱兑换
- 题目描述
- 代码与解题思路
- 57. 最小栈
- 题目描述
- 代码与解题思路
- 58. 最长有效括号
- 题目描述
- 代码与解题思路
- 59. 反转字符串中的单词
- 题目描述
- 代码与解题思路
- 60. 字符串相乘
- 题目描述
- 代码与解题思路
51. 缺失的第一个正数
题目链接:41. 缺失的第一个正数
题目描述

代码与解题思路
func firstMissingPositive(nums []int) int {
for i := 0; i < len(nums); i++ {
for nums[i] > 0 && nums[i] <= len(nums) && nums[i] != nums[nums[i]-1] {
nums[i], nums[nums[i]-1] = nums[nums[i]-1], nums[i]
}
}
for i := 0; i < len(nums); i++ {
if nums[i] != i+1 {
return i+1
}
}
return len(nums)+1
}
这道题不难做,难在怎么用 O(N) 的时间复杂读和 O(1) 的空间复杂度来做,如果忽略这两个条件,可以用排序二分,可以用哈希存储
而想要达成这个复杂度的目标,就必须用原地哈希来做,而具体思路就是这个哥们的神之比喻:

52. 训练计划 II
题目链接:LCR 140. 训练计划 II
题目描述

代码与解题思路
func trainingPlan(head *ListNode, cnt int) *ListNode {
slow, fast := head, head
for fast != nil && cnt > 0 {
fast = fast.Next
cnt--
}
for fast != nil {
slow = slow.Next
fast = fast.Next
}
return slow
}
这道题刷的次数太多太多,一看到 DNA 都动了,直接快慢指针,fast 先走 cnt 步,然后再一起走就行了。
53. 子集
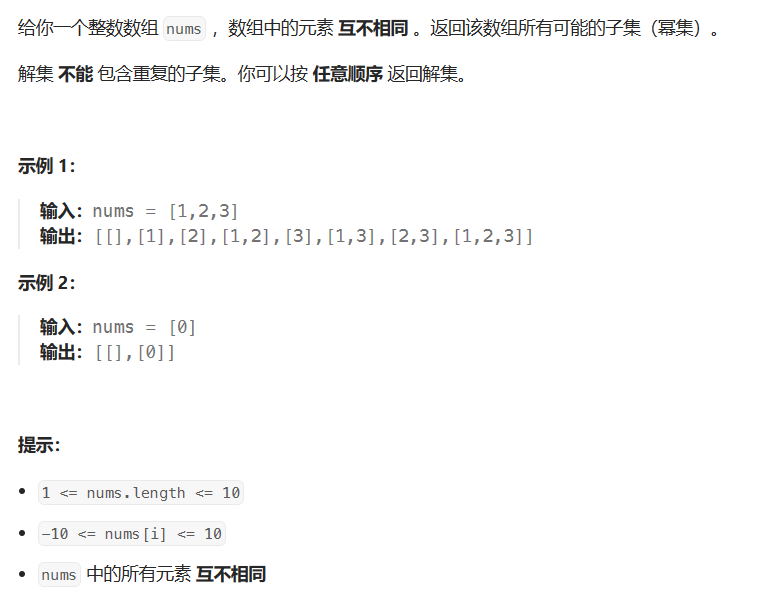
题目链接:78. 子集
题目描述
代码与解题思路
func subsets(nums []int) (ans [][]int) {
tmp := []int{}
var dfs func(int)
dfs = func(start int) {
ans = append(ans, append([]int(nil), tmp...))
for i := start; i < len(nums); i++ {
tmp = append(tmp, nums[i])
dfs(i+1)
tmp = tmp[:len(tmp)-1]
}
}
dfs(0)
return ans
}
经典的 dfs 模板题,求子集;还有一个模板是 dfs 求全排列,前段时间刷过。
54. 最小覆盖子串
题目链接:76. 最小覆盖子串
题目描述

代码与解题思路
func minWindow(s string, t string) string {
if len(s) < len(t) {
return ""
}
win := map[byte]int{}
cmp := map[byte]int{}
// 初始化 cmp
for i, _ := range t {
cmp[t[i]]++
}
start, end, match, minLen := 0, 0, 0, 100010
for left, right := -1, 0; right < len(s); right++ {
// 1. 将 s[right] 加入区间
ch1 := s[right]
win[ch1]++
// 2. 更新状态
if win[ch1] == cmp[ch1] {
match++
}
// 3. 满足条件, 出窗口
for match == len(cmp) {
// 更新窗口长度的最小值
if right - left < minLen {
start, end = left, right
minLen = right - left
}
// 出窗口, 更新状态
left++
ch2 := s[left]
if win[ch2] == cmp[ch2] {
match--
}
win[ch2]--
}
}
return s[start+1:end+1]
}
这道题是典型的比较复杂的滑动窗口题目,考察对细节的把控,以及对滑动窗口算法思想的掌握程度,省流:考察基本功,我现在基本功也不够扎实,希望下一次能轻松写出这道题目
55. 从前序与中序遍历序列构造二叉树
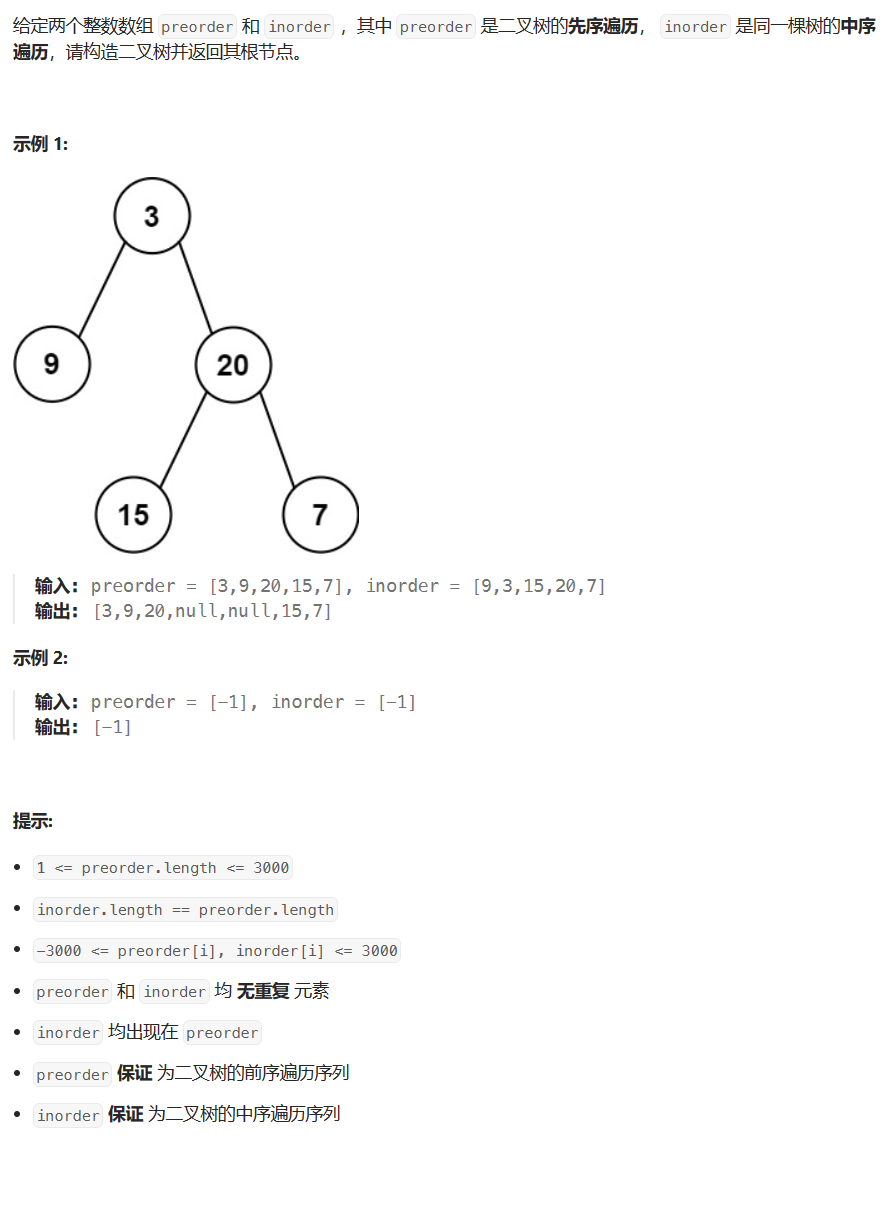
题目链接:105. 从前序与中序遍历序列构造二叉树
题目描述
代码与解题思路
func buildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder) == 0 {
return nil
}
root := &TreeNode{preorder[0], nil, nil}
i := 0
for i = 0; i < len(inorder); i++ { // 找到与前序遍历数对应的中序遍历数
if inorder[i] == preorder[0] {
break
}
}
root.Left = buildTree(preorder[1:len(inorder[:i])+1], inorder[:i]) // 构建左子树
root.Right = buildTree(preorder[len(inorder[:i])+1:], inorder[i+1:]) // 构建右子树
return root
}
这道题目的关键是得知道怎么用前序遍历和中序遍历的性质推出一棵树,只需要知道这一点,这道题就很好做了,具体来说就是根据两个性质:
- 前序遍历数组的第一个数就是根节点
- 中序遍历数组的数,在左边的就是在他的左子树,在右边就是在他的右子树,举个例子:

根节点 3,中序数组中,9 在 3 的左边,所以他在左子树,剩下的其他节点在右边,所以他们是右子树。
根据这两个性质,就能推出一整棵树了,也通过这个性质来构建一颗树。
56. 零钱兑换
题目链接:322. 零钱兑换
题目描述

代码与解题思路
func coinChange(coins []int, amount int) int {
dp := make([]int, amount+1)
for i, _ := range dp {
dp[i] = math.MaxInt
}
dp[0] = 0
for i := 0; i < len(coins); i++ {
for j := coins[i]; j <= amount; j++ {
if dp[j-coins[i]] != math.MaxInt {
dp[j] = min(dp[j], dp[j-coins[i]]+1)
}
}
}
if dp[amount] != math.MaxInt {
return dp[amount]
}
return -1
}
我背包问题没怎么学明白,看的这个哥们的思路:https://leetcode.cn/problems/coin-change/discussion/comments/79896
57. 最小栈
题目链接:155. 最小栈
题目描述

代码与解题思路
这道题真的只有做过才能想的出来,虽然我之前做过一次,但是现在已经忘记了,所以就先凭感觉刷了一遍;
type MinStack struct {
arr []int
min int
}
func Constructor() MinStack {
return MinStack{
arr: []int{},
min: math.MaxInt,
}
}
func (this *MinStack) Push(val int) {
if this.min > val {
this.min = val
}
this.arr = append(this.arr, val)
}
func (this *MinStack) Pop() {
top := this.arr[len(this.arr)-1]
this.arr = this.arr[:len(this.arr)-1]
if top == this.min {
minVal := math.MaxInt
for _, v := range this.arr {
minVal = min(minVal, v)
}
this.min = minVal
}
}
func (this *MinStack) Top() int {
return this.arr[len(this.arr)-1]
}
func (this *MinStack) GetMin() int {
return this.min
}
O(1) 取最小,O(N) 维护
之后看了一下官方题解,记忆回归:
type MinStack struct {
st1 []int
st2 []int
}
func Constructor() MinStack {
return MinStack {
st1: []int{},
st2: []int{math.MaxInt},
}
}
func (t *MinStack) Push(val int) {
t.st1 = append(t.st1, val)
t.st2 = append(t.st2, min(t.st2[len(t.st2)-1], val))
}
func (t *MinStack) Pop() {
t.st1 = t.st1[:len(t.st1)-1]
t.st2 = t.st2[:len(t.st2)-1]
}
func (t *MinStack) Top() int {
return t.st1[len(t.st1)-1]
}
func (t *MinStack) GetMin() int {
return t.st2[len(t.st2)-1]
}
官方给定的方法是,维护两个栈,一个栈正常放值,正常出值;另一个最小栈每次入栈都是最小值
58. 最长有效括号
题目链接:32. 最长有效括号
题目描述
代码与解题思路
用栈模拟:
func longestValidParentheses(s string) (ans int) {
st := []int{-1}
for i, v := range s {
if v == '(' {
st = append(st, i)
} else { // v == ')'
st = st[:len(st)-1]
if len(st) > 0 { // 栈不为空, 更新最大长度
ans = max(ans, i - st[len(st)-1])
} else { // 栈为空, 将')'对应的索引入栈作为新的参照物
st = append(st, i)
}
}
}
return ans
}
核心思想:
- 保留一个参照位置,通过当前索引值 - 参照位置的索引求出最长括号的长度,参照位置初识为 -1,之后为初识位置的前一个位置
- 当 v == ‘(’ 时入栈,遇到 ‘)’ 出栈匹配,并更新最长长度,当遇到 ‘)’ 而没有 ‘(’ 匹配的话,就让它作为新的参照物
其实还有动态规划的解法,但是对我现在来说太难了
59. 反转字符串中的单词
题目链接:151. 反转字符串中的单词
题目描述

代码与解题思路
func reverseWords(s string) string {
s = strings.TrimSpace(s)
left, right := len(s)-1, len(s)-1
resSlice := make([]string, 0)
for left >= 0 {
// left 找单词左边界
for left >= 0 && s[left] != ' ' {
left--
}
resSlice = append(resSlice, s[left+1:right+1])
// left 跳过空格
for left >= 0 && s[left] == ' ' {
left--
}
right = left
}
return strings.Join(resSlice, " ")
}
这道题主要是用了 s = strings.TrimSpace(s),以及 strings.Join(resSlice, " ") 两个字符串相关的 api,之后我会总结一份 Golang 专属的刷算法 api 库,到时候会收录进去的
60. 字符串相乘
题目链接:43. 字符串相乘
题目描述

代码与解题思路
func multiply(num1 string, num2 string) string {
if num1 == "0" || num2 == "0" {
return "0"
}
ans := "0"
m, n := len(num1), len(num2)
for i := n - 1; i >= 0; i-- {
curr := ""
add := 0
for j := n - 1; j > i; j-- { // 竖式乘法, 每乘一个数后面会多一个 0
curr += "0"
}
y := int(num2[i] - '0')
for j := m - 1; j >= 0; j-- {
x := int(num1[j] - '0')
product := x * y + add
curr = strconv.Itoa(product % 10) + curr // 把新计算的数拼接到 curr 前面
add = product / 10
}
if add != 0 { // 处理最后一次进位
curr = strconv.Itoa(add % 10) + curr
}
ans = addStrings(ans, curr)
}
return ans
}
func addStrings(num1, num2 string) string { // 竖式乘法的每一轮相加
i, j := len(num1) - 1, len(num2) - 1
add := 0
ans := ""
for ; i >= 0 || j >= 0 || add != 0; i, j = i - 1, j - 1 {
x, y := 0, 0
if i >= 0 {
x = int(num1[i] - '0')
}
if j >= 0 {
y = int(num2[j] - '0')
}
result := x + y + add
ans = strconv.Itoa(result % 10) + ans
add = result / 10
}
return ans
}
这道题不简单,但并不是不能做,一定要做好分析,正确的模拟竖式乘法的过程,主要是分为两个步骤,一个是对竖式乘法每一行乘积的模拟,一个是将竖式乘法每一行的乘积相加的模拟,把这两个核心步骤实现了,这道题目就做出来了
考察的是对字符串操作和代码的把控能力,现在我的代码把控能力还没有非常的强,我希望寒假的这一个月能有一个不小的进步